深度学习基础之线性回归
深度学习基础之线性回归
【代码】
1. 线性回归的基本要素
以⼀个简单的房屋价格预测作为例⼦来解释线性回归的基本要素。假设价格只取决于房屋状况的两个因素,即面积(平方米)和房龄(年)。接下来我们希望探索价格与这两个因素的具体关系。
模型:
设房屋的面积为 x 1 x_1 x1,房龄为 x 2 x_2 x2,售出价格为 y y y。建立基于输入 x 1 x_1 x1和 x 2 x_2 x2来计算输出 y y y的表达式,也就是模型(model)。顾名思义,线性回归假设输出与各个输入之间是线性关系:
y ^ = x 1 w 1 + x 2 w 2 + b (1) \hat{y}=x_1w_1+x_2w_2+b \tag 1 y^=x1w1+x2w2+b(1)
其中 w 1 w_1 w1和 w 2 w_2 w2是权重(weight), b b b是偏差(bias),且均为标量。它们是线性回归模型的参数(parameter)。模型输出 y ^ \hat{y} y^是线性回归对真实价格 y y y的预测或估计。我们通常允许它们之间有一定误差。
模型训练:
通过数据来寻找特定的模型参数值,使模型在数据上的误差尽可能小。
训练数据:
假设采集的样本集为 n n n,索引为 i i i的样本的特征为 x 1 ( i ) x_1^{(i)} x1(i)和 x 2 ( i ) x_2^{(i)} x2(i),标签为 y ( i ) y^{(i)} y(i)。对于索引为 i i i的房屋,线性回归模型的房屋价格预测表达式为:
y ( i ) ^ = x 1 ( i ) w 1 + x 2 ( i ) w 2 + b (2) \hat{y^{(i)}}=x_1^{(i)}w_1+x_2^{(i)}w_2+b \tag 2 y(i)^=x1(i)w1+x2(i)w2+b(2)
损失函数:
⽤训练数据集中所有样本误差的平均来衡量模型预测的质量,即:
l ( w 1 , w 2 , b ) = 1 n ∑ i = 1 n l ( i ) ( w 1 , w 2 , b ) = 1 n ∑ i = 1 n 1 2 ( x 1 ( i ) w 1 + x 2 ( 2 ) w 2 + b − y ( i ) ) 2 (3) l(w_1,w_2,b)=\frac{1}{n}\sum_{i=1}^{n} l^{(i)}(w_1,w_2,b)=\frac{1}{n}\sum_{i=1}^{n} \frac{1}{2}(x_1^{(i)}w_1+x_2^{(2)}w_2+b-y^{(i)})^2 \tag 3 l(w1,w2,b)=n1i=1∑nl(i)(w1,w2,b)=n1i=1∑n21(x1(i)w1+x2(2)w2+b−y(i))2(3)
在模型训练中,找出一组模型参数,记为 w 1 ∗ , w 2 ∗ , b ∗ w_1^{*},w_2^{*},b^{*} w1∗,w2∗,b∗,来使训练样本平均损失最小:
w 1 ∗ , w 2 ∗ , b ∗ = arg min w 1 , w 2 , b l ( w 1 , w 2 , b ) (4) w_1^{*},w_2^{*},b^{*}=\arg\min_{w_1,w_2,b}l(w_1,w_2,b) \tag 4 w1∗,w2∗,b∗=argw1,w2,bminl(w1,w2,b)(4)
解析解与数值解:
当模型和损失函数形式较为简单时,上⾯的误差最小化问题的解可以直接⽤公式表达出来。这类解叫作解析解(analytical solution)。本节使⽤的线性回归和平⽅误差刚好属于这个范畴。然而,⼤多数深度学习模型并没有解析解,只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解(numerical solution)。
小批量随机梯度下降:
先选取⼀组模型参数的初始值,如随机选取;接下来对参数进⾏多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样⼀个由固定数目训练数据样本所组成的小批量(mini-batch)B,然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后用此结果与预先设定的⼀个正数的乘积作为模型参数在本次迭代的减小量。
迭代过程:
β ← w 1 − η ∣ B ∣ ∑ i ∈ B ∂ l ( i ) ( w 1 , w 2 , b ) ∂ β ( β = ( w 1 , w 2 , b ) (5) \beta \leftarrow w_1 - \frac{\eta}{|B|} \sum_{i \in B}\frac{\partial{l^{(i)}(w_1,w_2,b)}}{\partial \beta}(\beta=(w_1,w_2,b) \tag 5 β←w1−∣B∣ηi∈B∑∂β∂l(i)(w1,w2,b)(β=(w1,w2,b)(5)
其中, ∣ B ∣ |B| ∣B∣代表每个小批量中的样本个数(批量大小,batch_size), η \eta η称作学习率(learning rate)并取正数。
超参数:
批量大小和学习率的值是人为设定的,并不是通过模型训练学出的。通常所说的“调参”指的正是调节超参数,例如通过反复试错来找到超参数合适的值。
模型预测:
模型训练完成之后,将模型参数 w 1 , w 2 , b w_1,w_2,b w1,w2,b在优化算法停止时的值分别记作 w 1 ^ , w 2 ^ , b ^ \hat{w_1},\hat{w_2},\hat{b} w1^,w2^,b^。注意,这⾥我们得到的并不⼀定是最小化损失函数的最优解 w 1 ^ , w 2 ^ , b ^ \hat{w_1},\hat{w_2},\hat{b} w1^,w2^,b^,而是对最优解的⼀个近似。然后,我
们就可以使⽤学出的线性回归模型 x 1 w 1 ^ + x 2 w 2 ^ + b ^ x_1\hat{w_1}+x_2\hat{w_2}+\hat{b} x1w1^+x2w2^+b^来估算训练数据集以外任意一栋面积(平方米)为 x 1 x_1 x1、房龄(年)为 x 2 x_2 x2的房屋的价格。
2. 线性回归的表示方法
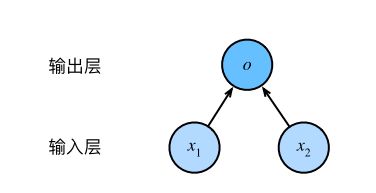
2.1 神经网络图
如图所示的神经网络中,输入分别为 x 1 x_1 x1和 x 2 x_2 x2,因此输入层的输入个数为2。输入个数也叫特征数或特征向量维度。
网络中的输出为 o o o,即 y ^ = o \hat{y}=o y^=o。由于输入层并不涉及计算,该神经网络的层数为1。
所以,线性回归是一个单层神经网络。输出层中负责计算 o o o的单元又叫神经元。在线性回归中, o o o的计算依赖于 x 1 x_1 x1和 x 2 x_2 x2。也就是说,输出层中的神经元和输⼊层中各个输⼊完全连接。因此,这⾥的输出层⼜叫全连接层(fully-connected layer)或稠密层(dense layer)。
2.2 矢量计算表达式
在模型训练或预测时,我们常常会同时处理多个数据样本并用到矢量计算。
import mxnet as mx # 导入mxnet框架
from time import time # 导入计时模块
a = mx.nd.ones(shape=1000)
b = mx.nd.ones(shape=1000)
# 向量按元素逐一相加
start = time()
c = mx.nd.zeros(shape=1000)
for i in range(1000):
c[i] = a[i] + b[i]
time() - start
0.26018500328063965
# 向量直接做矢量相加
start = time()
d = a + b
time() - start
0.0
3. 线性回归从零开始实现
# 导包
%matplotlib inline
from IPython import display
from matplotlib import pyplot as plt
import random
# 生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = mx.nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += mx.nd.random.normal(scale=0.01,shape=labels.shape)
# 查看features
features[0],labels[0]
(
[1.1630785 0.4838046]
,
[4.879625]
)
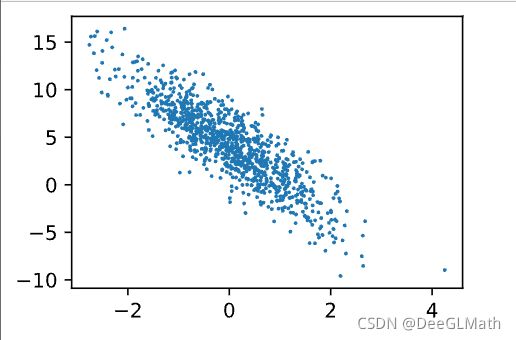
# ⽣成第⼆个特征features[:, 1]和标签 labels 的散点图
def use_svg_display():
# 用矢量图显示
display.set_matplotlib_formats('svg')
# 设置绘图尺寸
def set_figsize(figsize=(3.5,2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['figure.figsize'] = figsize
set_figsize()
plt.scatter(features[:,1].asnumpy(),labels.asnumpy(),1);
C:\Users\林景\AppData\Local\Temp/ipykernel_10068/2248800434.py:4: DeprecationWarning: `set_matplotlib_formats` is deprecated since IPython 7.23, directly use `matplotlib_inline.backend_inline.set_matplotlib_formats()`
display.set_matplotlib_formats('svg')
# 读取数据(读取小批量样本)
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本读取顺序随机
for i in range(0, num_examples, batch_size):
j = mx.nd.array(indices[i : min(i + batch_size, num_examples)])
yield features.take(j), labels.take(j) # take函数根据索引返回对应元素
batch_size = 10
for X , y in data_iter(batch_size, features, labels):
print(X, y)
break
[[-0.9634816 -0.1391419 ]
[-0.19690166 -1.5063294 ]
[ 1.7697632 -0.01087634]
[-1.106382 0.03557368]
[ 2.1034694 -1.0703046 ]
[ 1.527508 -0.42868343]
[-2.0252197 0.14331104]
[-0.8330337 -1.9252781 ]
[ 1.5200766 0.2755394 ]
[ 1.6553524 2.009465 ]]
[ 2.7542405 8.929056 7.7738566 1.8779316 12.02442 8.719315
-0.34202975 9.080867 6.2904167 0.6711063 ]
# 初始化模型参数
w = mx.nd.random.normal(scale=0.01, shape=(num_inputs, 1)) # 均值为0、标准差为0.01的正态随机数
b = mx.nd.zeros(shape=(1, )) # 偏差则初始化0
# 创建参数的梯度
w.attach_grad()
b.attach_grad()
# 定义模型
def linreg(X, w, b):
return mx.nd.dot(X, w) + b
# 定义损失函数
def squared_loss(y_hat, y):
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
# 定义优化算法
def sgd(params, lr, batch_size):
for param in params:
param[:] = param - lr * param.grad / batch_size
# 训练模型
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每⼀个迭代周期中,会使⽤训练数据集中所有样本⼀次(假设样本数能够被批量⼤⼩整除)
# X和y分别是小批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
with mx.autograd.record():
l = loss(net(X, w, b), y) # l是有关小批量X和y的损失
l.backward() # 小批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使⽤⼩批量随机梯度下降迭代模型参数
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))
epoch 1, loss 0.035079
epoch 2, loss 0.000127
epoch 3, loss 0.000048
# 比较系数
true_w, w
([2, -3.4],
[[ 1.9996246]
[-3.3997977]]
)
# 比较截距
true_b, b
(4.2,
[4.200065]
)
4. 线性回归的简洁实现
# 生成数据集
from mxnet import autograd, nd
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
# 读取数据
from mxnet.gluon import data as gdata
batch_size = 10
# 将训练数据的特征和标签组合
dataset = gdata.ArrayDataset(features, labels)
# 随机读取小批量
data_iter = gdata.DataLoader(dataset, batch_size, shuffle=True)
# 读取并打印第一个小批量数据样本
for X, y in data_iter:
print(X, y)
break
[[ 0.2821344 0.16764306]
[-0.8777253 0.85446167]
[-0.02137053 -0.341217 ]
[ 0.61804163 0.27122775]
[ 0.5660121 -1.0838059 ]
[-1.4270303 0.4062857 ]
[-1.2657014 0.7512132 ]
[-0.15702339 -0.36244255]
[ 0.92926574 -0.80137885]
[ 0.44107556 0.25636742]]
[ 4.1896577 -0.4419743 5.3333077 4.517534 9.023388 -0.02928578
-0.87772304 5.110723 8.798182 4.2165217 ]
# 定义模型
"""定义⼀个模型变量net,它是⼀个Sequential实例。在Gluon中,Sequential实例
可以看作是⼀个串联各个层的容器。在构造模型时,我们在该容器中依次添加
层。当给定输⼊数据时,容器中的每⼀层将依次计算并将输出作为下⼀层的输⼊。"""
from mxnet.gluon import nn
net = nn.Sequential()
net.add(nn.Dense(1))
# 初始化模型参数
"""通过init.Normal(sigma=0.01)指定权重参数每个元素将在初始化时随机采样于
均值为0、标准差为0.01的正态分布。偏差参数默认会初始化为零。"""
from mxnet import init
net.initialize(init.Normal(sigma=0.01))
# 定义损失函数
from mxnet.gluon import loss as gloss
loss = gloss.L2Loss() # 平方损失又称L2范数损失
# 定义优化算法
from mxnet import gluon
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.03})
# 训练模型
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
l = loss(net(features), labels)
print('epoch %d, loss: %f' % (epoch, l.mean().asnumpy()))
epoch 1, loss: 0.055379
epoch 2, loss: 0.000255
epoch 3, loss: 0.000050
# 观察系数
dense = net[0]
true_w, dense.weight.data()
([2, -3.4],
[[ 1.9997329 -3.3994622]]
)
# 观察截距
true_b, dense.bias.data()
(4.2,
[4.198708]
)