量子遗传算法

量子遗传算法概述

量子遗传算法( QGA )是量子计算与遗传算法相结合的产物，是一种新发展起来的概率进化方法。

GA会由于选择、交叉或变异等方式的不当而出现迭代次数多、收敛速度慢、容易陷入局部极值的现象。

量子计算中采用量子态作为基本的信息单元，利用量子态的叠加、纠缠和干涉等特性，通过量子并计算可以解决经典计算中的NP问题。

QGA即为将量子的态矢量表达式引入遗传编码，利用量子逻辑门实现染色体的演化，实现了比SGA更好的效果。

量子比特编码

在量子计算机中，充当信息存储单元的物理介质是一个双态量子系统，称为量子比特。量子比特与经典位不同就在于它可以同时处在两个量子态的叠加态中，比如：
$$\mid \phi ⟩=\alpha \mid 0⟩+\beta \mid 1⟩$$
(α，β)是两个幅常数，满足
$${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$$
其中，$\mid 0⟩$和$\mid 1⟩$分别表示自旋向上和自旋向上态。所以一个量子比特可同时包含$\mid 0⟩$和$\mid 1⟩$的信息。

在量子遗传算法中，采用量子比特存储和表达一个基因。该基因可以为“0”态或“1”态，或它们的任意叠加态。即该基因所表达的不再是某一个确定的信息。而是包含所有可能的信息，对该基因的任意操作也会同时作用于所有可能的信息。

采用量子比特编码使得一个染色体可以同时表达多个态的叠加，使得量子遗传算法比经典遗传算法拥有更好的多样性特征。采用量子比特编码也可以获得较好的收敛性，随着${\left|\alpha \right|}^2$或$\left |\beta \right |^{2} $趋于0或1，量子比特编码的染色体将收敛到一个单一态。

案例分析

$$\max f(x，y)=21。5+x\sin (4\pi x)+y\sin (20\pi y)$$

KaTeX parse error: Undefined control sequence: \ at position 31: …。0\ll x\ll 12。1\̲ ̲ \\4。1\ll y \ll…

由于目标函数中含有振荡变换的sin函数，通常的寻优算法容易陷入局部极值或在局部极值间振荡，故其适用于验证量子遗传算法的性能。

算法流程

1. 初始化种群Q(t0)，随机生成n个以量子比特为编码的染色体；
2. 对初始种群Q(t0)中的每个个体进行一次测量，得到对应的确定解P(to)；
3. 对各确定解进行适应度评估；
4. 记录最优个体和对应的适应度；
5. 判断计算过程是否可以结束，若满足结束条件则退出，否则继续计算；
6. 对种群Q(t)中的每个个体实施一次测量，得到相应的确定解；
7. 对各确定解进行适应度评估；
8. 利用量子旋转门U(t)对个体实施调整，得到新的种群Q(t+1)；
9. 记录最优个体和对应的适应度；
10. 将迭代次数t加1，返回步骤5。

代码实现

量子旋转门函数：

function chrom=Qgate(chrom,fitness,best,binary)
%% 量子旋转门调整策略
% 输入  chrom：更新前的量子比特编码
%     fitness：适应度值
%        best：当前种群中最优个体
%      binary：二进制编码
% 输出  chrom：更新后的量子比特编码
sizepop=size(chrom,1)/2;
lenchrom=size(binary,2);
for i=1:sizepop
    for j=1:lenchrom
        A=chrom(2*i-1,j);   % α
        B=chrom(2*i,j);     % β
        x=binary(i,j);
        b=best.binary(j);
        if ((x==0)&(b==0))||((x==1)&(b==1))
            delta=0;                  % delta为旋转角的大小
            s=0;                        % s为旋转角的符号，即旋转方向
        elseif ...
        
        end
        e=s*delta;       % e为旋转角
        U=[cos(e) -sin(e);sin(e) cos(e)];      % 量子旋转门
        y=U*[A B]';        % y为更新后的量子位
        chrom(2*i-1,j)=y(1);
        chrom(2*i,j)=y(2);
    end
end

主函数：

%----------------参数设置-----------------------
MAXGEN=200;                        % 最大遗传代数
sizepop=40;                        % 种群大小
lenchrom=[20 20];          % 每个变量的二进制长度
trace=zeros(1,MAXGEN);
%-------------------------------------------------------------------------- 

best=struct('fitness',0,'X',[],'binary',[],'chrom',[]);   % 最佳个体 记录其适应度值、十进制值、二进制编码、量子比特编码
%% 初始化种群
chrom=InitPop(sizepop*2,sum(lenchrom));
%% 对种群实施一次测量 得到二进制编码
binary=collapse(chrom); 
%% 求种群个体的适应度值，和对应的十进制值
[fitness,X]=FitnessFunction(binary,lenchrom);         % 使用目标函数计算适应度
%% 记录最佳个体到best
[best.fitness bestindex]=max(fitness);     % 找出最大值
best.binary=binary(bestindex,:);
best.chrom=chrom([2*bestindex-1:2*bestindex],:);
best.X=X(bestindex,:);
trace(1)=best.fitness;
fprintf('%d\n',1)

%% 进化
for gen=2:MAXGEN
    fprintf('%d\n',gen)  %提示进化代数
    %% 对种群实施一次测量
    binary=collapse(chrom);
    %% 计算适应度
    [fitness,X]=FitnessFunction(binary,lenchrom);
    %% 量子旋转门
    chrom=Qgate(chrom,fitness,best,binary);
    [newbestfitness,newbestindex]=max(fitness);    % 找到最佳值
    % 记录最佳个体到best
    if newbestfitness>best.fitness
        best.fitness=newbestfitness;
        best.binary=binary(newbestindex,:);
        best.chrom=chrom([2*newbestindex-1:2*newbestindex],:);
        best.X=X(newbestindex,:);
    end
    trace(gen)=best.fitness;
end

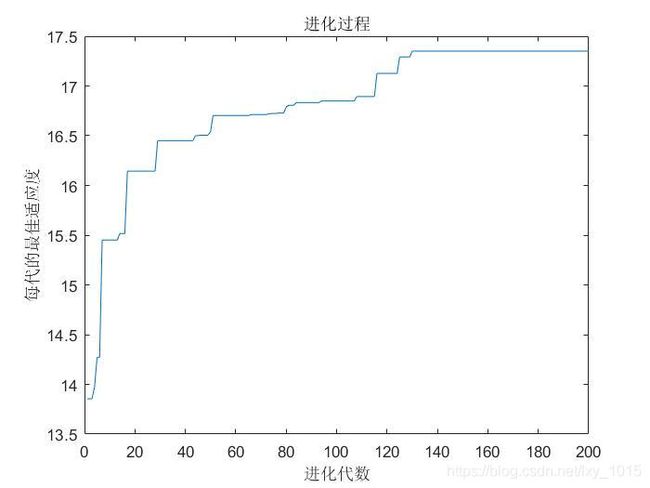
%% 画进化曲线
plot(1:MAXGEN,trace);
title('进化过程');
xlabel('进化代数');
ylabel('每代的最佳适应度');

%% 显示优化结果
disp(['最优解X：',num2str(best.X)])
disp(['最大值Y:',num2str(best.fitness)]);

上面为量子遗传算法的量子旋转门函数和主函数，其中还包含种群初始化函数、测量函数、适应度函数，它们的作用分别为得到初始种群的量子比特编码矩阵、对种群实施一次测量，得到二进制编码、得到函数适应度值和十进制数。

结果分析

迭代200次的进化过程如图所示：

最优解x=11.6255，y=5.72504；

最大值f(x)=17.3503

---

需要源码请在文章下留言