【动手学深度学习PyTorch版】4 多层感知机 + 代码实现
上一篇移步【动手学深度学习】3 Softmax 回归 + 损失函数_水w的博客-CSDN博客
目录
◼ softlabel的训练策略
一、感知机
1.1 感知机
◼ 感知机
◼ 训练感知机
1.2 感知机的收敛定理
1.3 感知机的问题:XOR问题
1.4 感知机总结
二、多层感知机
2.1 多层感知机:n * 激活函数(加权和)
◼ 多层感知机解决XOR问题
2.2 单隐藏层-单分类
2.3 多层感知机-多类分类
◼ 多层感知机总结
2.4 常用的激活函数:sigmoid(指数运算)、tanh、ReLU(计算快,指数运算百倍代价于乘法)
◼ Sigmoid 函数(指数运算)
◼ Tanh函数
◼ ReLU(计算快,指数运算百倍代价于乘法)
2.5 多层感知机代码实现
◼ 使用自定义
完整代码:
◼ 使用框架
完整代码:
◼ softlabel的训练策略
用一位有效来表示一个标号,有n类的话就变成一个很长的向量, 其中只有正确的那一类为1,其余都是0。然后所以我们用softmax来逼近纯0和1的分布。
但是问题是,如果用指数,很难用指数去逼近一个1。—— softmax逼近0和1是很难的(指数函数)。
softlabel的训练策略:一位有效(1)的向量表示类别(不正确的类使用0),预测时使用概率表示类别。
一、感知机
1.1 感知机
◼ 感知机
与线性回归不一样,线性回归输出的是一个实数,softmax回归输出概率,而感知机输出的是一个离散的类。
如果是一个二分类问题,那么感知机输出的是-1或1。
◼ 训练感知机
① 如果分类正确的话y
② 如果分类错了,y
其实就等价于使用一个批量大小为1的梯度下降,max(0,-y_hat) —— 直达所有都分类正确。
![]()
现在,假设来了一只新的狗,那么画出来的线---分割面就会发现对新样本分类分错了,就会进行更新,不断进行。
那么就有一个奇怪的停止条件:我必须把所有的样本都看完,对所有的样本分类都正确,才会停止。
1.2 感知机的收敛定理
感知机是一个简单的模型,所以有一个很好的收敛定理。所谓的收敛定理是说我什么时候可以停止,是不是真的可以停。
假设数据都在半径为r的区域里,假设有一个分截面可以使得所有的样本分类都正确,而且是有一定余量P的。那么这种情况下,感知机确信能够找到最优解。
- r:数据大小,如果很大的话,收敛速度会变慢;
- P:看数据是不是很好,很好的时候,数据的点就会分的很开。如果分割面特别的小,那么就需要花费很多的时间去找。
1.3 感知机的问题:XOR问题
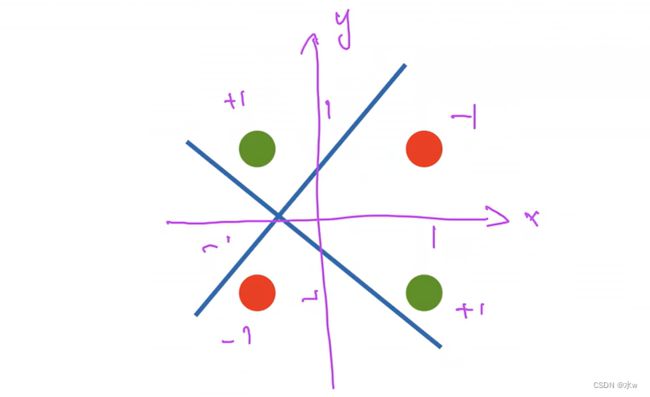
不能拟合XOR函数,如果是二维的输入,那么感知机的分割面是一条线, 只能产生线性分割面。那么就会是的必然有一个类(红色或绿色)被分错。
XOR函数(异或)就是说,
- 当输入的x和y都是1的时候,x和y相同,是-1类;
- 当输入的x和y不同时,是+1类;
导致了AI的一个寒冬。。。
1.4 感知机总结
二、多层感知机
2.1 多层感知机:n * 激活函数(加权和)
◼ 多层感知机解决XOR问题
- 第一步,我们先学习一条蓝色的线,使得绿1和红3分为一类,绿4和红2分为一类。
- 第二步,我们学习一条黄色的线,使得绿1和红2分为一类,绿4和红3分为一类。
- 最后,再对蓝色的线和黄色的线分出来的结果做乘法。
2.2 单隐藏层-单分类
隐藏层的大小是一个超参数。
输入层:n维向量
输出层:单分类,是一个标量O
那么,为什么我们需要非线性激活函数?
假设激活函数是本身的话,也就是说σ(x)=x,那么
不用激活函数的话,n个全连接层连接在一起依旧可以用一个最简单的线性函数来表示。
如果没有非线性激活函数:结果会等价于简单的线性模型!!!
2.3 多层感知机-多类分类
假设我要做K分类,就是要输出k个元素,想要得到置信度的话,就放到softmax(o1,o2......ok)的操作子里去,把所有的值拉到0-1的区域里去,让y1+y2....+yk=1。
多类分类和softmax没什么区别,唯一加的就是中间的隐藏层,
- 没加中间的隐藏层,就是softmax;
- 加了中间的隐藏层之后,就会变成多层感知机,也就是说在softmax里多加了一层;
多层感知机-多类分类的定义也和softmax没什么大区别,区别就是:
- 输出层为mxk的一个矩阵,从向量变成了矩阵;
- 偏移bais也变成一个长为k的向量,从标量变成了向量;
- 对output来讲,还需要做softmax;
那就是说,我也可以做多隐藏层,隐藏层的层数是一个超参数。
数学上来说,每一个隐藏层都有自己的权重W和偏移b,第一个隐藏层的输出就会进入下一层作为第二个隐藏层的输入,会跟权重做乘法,再加上偏移,再做一次激活函数,以此类推。
激活函数不能少,如果少了一个,那么本质上层次就会减一。主要是避免我们层数的塌陷,输出层不需要激活函数。
一般来说,有一些技术上的经验总结:
层数越多肯定模型越复杂。所以一般先感觉一下输入的复杂对会有多少,假设你就觉得这个数据比较难的话,线性模型先不考虑,假设我想要多层感知机,那么有2个选择:
- 用单隐藏层,把m设的稍微大一些。假设输入维度128,那么隐藏层可以做64或128甚至256;
- 把模型做的深一些,3个隐藏层,如果隐藏层的大小为128的话,那么相对于单隐藏层,我们的3个隐藏层,隐藏层m1的大小肯会相对128小一点,隐藏层m2会比隐藏层m1小一些,那么隐藏层m3会比隐藏层m2小一些;
为什么这么说呢?假设数据比较复杂,那么通常来说维度是比较高的,比如128或者256。那么输出相对来说是比较少的,比如10类。
比如说图片的压缩,把一个很复杂的图片压缩到5或者10维的一个简单的输出上,最好是慢慢把图片压缩,比如128---->64---->32---->16---->8---->5,不断地把信息进行提炼。
如果很快速的话,可能能会损失一些信息,后面再还原是比较难的。
◼ 多层感知机总结
2.4 常用的激活函数:sigmoid(指数运算)、tanh、ReLU(计算快,指数运算百倍代价于乘法)
◼ Sigmoid 函数(指数运算)
Sigmoid 函数其实是一个比较平和的softmax版本,具体的定义就是:
◼ Tanh函数
◼ ReLU(计算快,指数运算百倍代价于乘法)
σ(x)=x线性的肯定是不行,那么怎么把线性去掉呢?
ReLU左侧的导数是0,右侧的导数是+1。
① ReLU的好处在于不需要执行指数运算。
② 在CPU上一次指数运算相当于上百次乘法运算。
2.5 多层感知机代码实现
◼ 使用自定义
(1)实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元,
- 这里的输入、输出是数据决定的,256是调参自己决定的,取了一个在784和10之间的数。
- W初始了一个随机的,它的行数是输入的个数784,列数是256,偏差是0;
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入、输出是数据决定的,256是调参自己决定的
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1,b1,W2,b2](2)实现ReLu 激活函数,求最大值,
# 实现 ReLu 激活函数
def relu(X):
a = torch.zeros_like(X) # 数据类型、形状都一样,但是值全为 0
return torch.max(X,a)(3)实现模型,
# 实现模型
def net(X):
#print("X.shape:",X.shape)
X = X.reshape((-1, num_inputs)) # 拉成二维矩阵,-1为自适应的批量大小,num_inputs=784
#print("X.shape:",X.shape)
H = relu(X @ W1 + b1) # 矩阵乘法:x为784,w为784x256,b1为256长的向量
#print("H.shape:",H.shape)
#print("W2.shape:",W2.shape)
return (H @ W2 + b2)(4)训练模型,多层感知机的训练过程与softmax回归的训练过程完全一样
# 损失
loss = nn.CrossEntropyLoss() # 交叉熵损失
# 多层感知机的训练过程与softmax回归的训练过程完全一样
num_epochs ,lr = 30, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)完整代码:
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入、输出是数据决定的,256是调参自己决定的
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1,b1,W2,b2]
# 实现 ReLu 激活函数
def relu(X):
a = torch.zeros_like(X) # 数据类型、形状都一样,但是值全为 0
return torch.max(X,a)
# 实现模型
def net(X):
#print("X.shape:",X.shape)
X = X.reshape((-1, num_inputs)) # -1为自适应的批量大小
#print("X.shape:",X.shape)
H = relu(X @ W1 + b1)
#print("H.shape:",H.shape)
#print("W2.shape:",W2.shape)
return (H @ W2 + b2)
# 损失
loss = nn.CrossEntropyLoss() # 交叉熵损失
# 多层感知机的训练过程与softmax回归的训练过程完全一样
num_epochs ,lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)在没有隐藏层之前,我们的损失大概是0.4,精度大概是0.8,有了隐藏层之后,我们这里图上的损失是比0.4低一些的,精度没有发生太多变化。
可以看到这个现象,多层感知机使得损失确实往下降了,因为我的模型更大了,所以拟合的更好了,所以损失在下降。但是精度没有发生太多变化,之后再来探讨这个问题。
◼ 使用框架
调用高级API更简洁地实现多层感知机。
完整代码:
import torch
from torch import nn
from d2l import torch as d2l
# 隐藏层包含256个隐藏单元,并使用了ReLU激活函数,输出长为10的标量
net = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight,std=0,)
net.apply(init_weights)
# 训练过程
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 用之前实现的函数把它存入d2l这个包里,进行调用
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)理论上结果与使用自定义的一样。