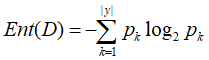数据科学/机器学习——特征选择【代码实例：银行电话营销】

特征选择

• 要求：在保证一定分类精度的前提下，减少特征维度【“降维”】，使分类器实现快速、准确和高效的分类【关键：所提供的识别特征具有很好的可分性，使分类器容易判别】

  • 应去掉模棱两可、不易判别的特征
  • 所提供的特征不重复【去掉相关性强且没有增加更多信息的特征】

• 特征选择

  • 从给定的特征集合中选出任务相关特征子集
  • 必须确保不丢失重要特征
  • 原因：减轻维度灾难、降低学习难度

• 特征选择的一般过程

  • 子集产生：根据某种策略产生候选的特征子集
    • 前向搜索：逐渐增加相关特征
    • 后向搜索：从完整的特征集合开始，组件减少特征
    • 双向搜索：每一轮逐渐增加相关特征，同时减少无关特征
  • 子集评估：使用某种评价函数对特征子集的优劣进行评估
    • 特征子集确定了对数据集的一个划分，每个划分区域对应着特征子集的某种取值；样本标记对应着对数据集的真实划分
    • 通过估算这两个划分的差异，与样本标记对应的划分的差异越小，说明当前特征子集越好
  • 停止条件：决定特征选择算法什么时候停止
  • 子集验证：对所选的特征子集验证其有效性
    

• 特征选择方法

  • 过滤式Relief方法
    • 先用特征选择过程过滤原始数据，再用过滤后的特征来训练模型；特征选择过程与后续学习器无关
    • 为每个初始特征赋予一个“相关统计量”，度量特征的重要性
    • 特征子集的重要性由子集中每个特征所对应的相关统计量之和决定
    • 设计一个阈值，然后选择比阈值大的相关统计量分量所对应的特征；或指定欲选取的特征个数，然后选择相关统计量分量最大的指定个数特征
    • 时间开销随采样次数以及原始特征数线性增长，运行效率很高
    • 相关统计量的确定
      • 猜中近邻【near-hit】：x_i的同类样本中的最近邻x_i,nh
      • 猜错近邻【near-miss】：x_i的异类样本中的最近邻x_i,nm
      • 相关统计量对应属性j的分量为
      • 相关统计量越大，属性j上，猜对近邻比猜错近邻越近，即属性j对区分对错越有用
    • 子集评价

      • 皮尔逊相关系数

        • 判断特征和目标特征之间线性关系的统计量

      • 信息熵

        • 特征子集A确定了对数据集D的一个划分
          • A上的取值将数据集D分为V份，每一份用D^v表示
          • Ent(D^v)表示D^v上的信息熵
        • 样本标记Y对应着对数据集D的真实划分
          • Ent(D)表示D上的信息熵

      • 特征子集A的信息增益

      • 距离计算

        • 好的特征子集：同类样本之间的距离尽可能近，不同样本之间距离尽可能远
  • 包裹式/封装式
    • 特征选择过程与模型训练过程相结合，特征子集训练得到的模型性能来评价特征子集
    • 性能最优、特征子集“量身定做”；需重复训练和测试，计算复杂度高、开销大、时间成本高
    • LVW（Las Vegas Wrapper）
      • 以最终分类器的误差作为特征子集的评价准则
      • 步骤
        • 在循环的每一轮随机产生一个特征子集
        • 在随机产生的特征子集上通过交叉验证推断当前特征子集的误差
        • 多次循环，在多个随机产生的特征子集中选择误差最小的特征值子集作为最终解
      • 若运行时间优先，则可能给不出解
    • 递归特征消除（RFE）
      • 目标：通过不断构建模型递归地删除特征，对特征权重进行排序
      • 赋权重→删除绝对权重最小的特征→不断重复迭代
      • RFE稳定性对特征进行评价的模型有很大关系，模型稳定则方法稳定
    • 评价标准
      • 准确率、召回率、AUC面积、赤池信息准则和贝叶斯信息准则
      • 赤池信息准则AIC
        
      • 贝叶斯信息准则BIC
        
      • 以上两个准则权衡了模型复杂度（参数个数）和模型拟合程度（利用最大似然函数值来表示）；选择AIC和BIC值小的模型或特征子集
      • BIC表达式中，惩罚项的权重随样本的增加而增加，当样本数较大时，与目标特征相关性小的特征将被踢出，从而降低了模型的复杂度
  • 嵌入式【经典：决策树算法】
    • 把特征选择和模型训练在同一过程中完成的方法，模型训练结束时，特征选择也同时完成
    • 决策树算法：节点分裂-某一特征分裂，节点分裂所选择的特征顺序即代表了特征在决策树模型下的重要程度
    • 正则化
      • 在模型中加入惩罚项，以避免模型过拟合；使用LASSO可以使某些特征的系数变为0
      • 将L₁范数替换L₂范数则有LASSO

• 代码 银行电话营销

  • 数据预处理

    • 17个特征：客户基本信息包括年龄、职业、婚姻状态、教育程度、房贷和个人贷款等；营销活动信息包括通话⽅式、通话次数和上次营销结果等；社会经济环境信息包括就业变化率、居民消费价格指数和消费者信息指数等。
      读取数据后需要先了解数据整体特征，使用data.info()函数观察可知，许多object类型的特征中都用unknown来表示缺失，所以需要做缺失值处理，同时有11个数据类型是object类型，需要进行数值化处理；使用data.describe()函数，观察各特征的常用统计量，可知数据间存在明显的量级差异，需要做标准化处理。

  • 缺失值处理

    • 使用DataFrame的select_dtypes方法指定object对象：
      object_data = data.select_dtypes(include=[‘object’])
      统计各特征缺失值数量：
      相对而言，education与default特征缺失值较多，可使用众数填补法；其他特征缺失值数量较少，可直接使用删除法处理。

  • One-hot编码与0-1标准化

    • 把object类型特征用one-hot变量来表示，同时将目标特征数值化，y特征的yes改为1，no改为0；0-1标准化。

  • 划分训练集和测试集

    • 以7:3比例随机地划分训练集和测试集：
      train_x,test_x,train_y,test_y=train_test_split(x,y,test_size=0.3, random_state=0)

  • 特征选择

    • 正则化模型

      • 1特征选择：特征选择采用L1正则化；
        选择不同惩罚系数对特征选择效果的影响，并在训练集上进行5折交叉验证以验证模型效果，baseline是用特征全集在训练集上进行5折交叉验证得到的模型平均准确率。
        
        横坐标：惩罚系数，纵坐标：交叉验证得到的平均准确率；蓝色折线：不同惩罚系数下应用特征子集的模型准确率，红色直线：应用特征全集在同样模型上得到的准确率；
        蓝线都在红线之上说明经过L1正则化特征选择后的模型效果更好，当惩罚系数为1.7时，模型效果最好，所以我们可以尝试用惩罚系数为1.7的L1正则化来进行特征选择。
      • 2在特征子集上建立模型：利用在特征选择中得到的最优子集建立模型；
        lsvc_l1 = LinearSVC(C=1.7, penalty=“l1”, dual=False).fit(train_x, train_y)
        pred=lsvc_l1.predict(test_x)
        

  • 树模型

    • 1特征选择：分别以Gini不纯度和Entropy为特征选择指标，并探讨选择不同特征个数对特征选择效果的影响，在训练集上进行5折交叉验证以验证模型效果，baseline是用特征全集在训练集上进行5折交叉验证得到的模型平均准确率。
      
      横坐标：特征个数，纵坐标：交叉验证得到的平均准确率；蓝色折线：不同特征个数下应用特征子集的模型准确率，红色直线：baseline-应用特征全集在同样模型上得到的准确率；左图：Gini不纯度为指标，右图：Entropy为指标；
      特征个数对特征选择的效果影响很大，在一些特征子集上（比如特征个数为2、5、6、55时），模型可以取得比baseline更好的效果；但在另一些特征子集上（比如特征个数为14、15、16时），模型效果反而降低了很多。当特征子集中包含2个特征时，模型效果最好，但特征个数太少时虽然准确率确实高，却会造成很低的F1值，因此选择以Entropy为指标得到的特征个数为6的特征子集为最优子集候选。
      

    • 2在特征子集上建立模型：利用在特征选择中得到的最优子集建立模型；
      在最优子集上建立ExtraTrees模型
      
      模型整体准确率为 88.74%,召回率达 96%。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import  preprocessing as prep
from sklearn.cross_validation import train_test_split
from sklearn import metrics
from sklearn.metrics import classification_report 
import tqdm
from sklearn import cross_validation
from sklearn.svm import LinearSVC
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import ExtraTreesClassifier

def data_preprocessing(data):
    # 找到object类型特征
    object_data = data.select_dtypes(include=['object'])
    object_columns = object_data.columns
    object_list = object_columns.tolist()
    # 统计各特征缺失值数量
    missing_list = []
    print("------------缺失值数量------------")
    for item in object_columns:
        try:
            missing_num = object_data[item].value_counts().loc['unknown']
            print("%s :"  %item, missing_num)
            missing_list.append(item)
        except Exception as e:
            print("%s :"  %item, '0')
    new_data=data[data["job"]!="unknown"][data["marital"]!="unknown"][data["housing"]!="unknown"][data["loan"]!="unknown"]
    # 舍弃一部分缺失样本
    new_data=data[data["job"]!="unknown"][data["marital"]!="unknown"][data["housing"]!="unknown"][data["loan"]!="unknown"]
    new_data.index=range(len(new_data))
    
    # 用众数填补数量多的缺失值
    new_data["default"].replace('unknown', new_data["default"].value_counts().index[0], inplace=True)
    new_data['education'].replace('unknown', new_data["education"].value_counts().index[0], inplace=True)

    # 把object类型特征用one-hot变量来表示
    object_list.remove("y")
    for item in object_list:
        dummies=pd.get_dummies(new_data[item],prefix=item)
        new_data=pd.concat([new_data,dummies],axis=1)
        del new_data[item]
    # 目标特征数值化
    new_data["label"]=0
    new_data["label"][new_data["y"]=="yes"]=1
    new_data["label"][new_data["y"]=="no"]=0
    del new_data["y"] 
    
    #0-1标准化
    x=new_data.copy()
    del x["label"]
    del x["duration"]
    y=new_data["label"]
    minmax_scale=prep.MinMaxScaler().fit( x[ x.columns])
    x[ x.columns]=minmax_scale.transform( x[ x.columns])
    
    # 随机地划分训练集和测试集
    train_x, test_x, train_y, test_y = train_test_split(x, y, test_size=0.3, random_state=0)
    
    return train_x, test_x, train_y, test_y

"""
函数evaluate(pred,test_y)用来对分类结果进行评价；
输入：真实的分类、预测的分类结果
输出：分类的准确率、混淆矩阵等
"""
def evaluate(pred,test_y):
    
    # 输出分类的准确率
    print("Accuracy: %.4f"  % (metrics.accuracy_score(test_y,pred)))
    
    # 输出衡量分类效果的各项指标
    print(classification_report(test_y, pred)) 
    
    # 更直观的，我们通过seaborn画出混淆矩阵
#    %matplotlib inline
    plt.figure(figsize=(6,4))
    colorMetrics = metrics.confusion_matrix(test_y,pred)
    
    # 坐标y代表test_y，即真实的类别，坐标x代表估计出的类别pred
    sns.heatmap(colorMetrics,annot=True,fmt='d',xticklabels=[0,1],yticklabels=[0,1])
    plt.show()
    
"""
函数find_name(new_feature, df_feature)用来输出关键特征的名称；
输入：原始特征、选择的关键特征；
输出：关键特征的名称
"""
def find_name(new_feature, df_feature):
    
    # 定义列表存储关键特征名称
    feature_name=[]
    col=df_feature.columns
    
    # 寻找关键特征的名称信息
    for i in range(int(new_feature.shape[0])):
        for j in range(df_feature.shape[1]):
            
            # 判别标准为new_feature中的特征向量与df_feature中的特征向量一致
            if np.mean(abs(new_feature[i]-df_feature[col[j]]))==0:
                feature_name.append(col[j])
                print(i+1,col[j]) 
                break
    return feature_name

"""
函数FS_importance(arr_importance, col, N)用来根据特征重要性选择特征
输入：特征重要性、特征名称集、选择的特征个数
输出：根据特征重要性求出来的前N个特征
"""
def FS_importance(arr_importance, col, N):
    
    # 字典存储    
    dict_order=dict(zip(col, arr_importance))
    
    # 按特征重要性大小排序
    new_feature=sorted(dict_order.items(),key=lambda item:item[1], reverse=True)
    feature_top, score=zip(*new_feature)
    return list(feature_top[:N])

def select(train_x,train_y):
    # 定义不进行正则化的模型
    lsvc = LinearSVC(C=1e-5)
    
    # 交叉验证计算应用特征全集的平均准确率
    score=cross_validation.cross_val_score(lsvc, train_x, train_y, cv=5)
    
    # 探讨不同参数对特征选择效果的影响
    # xx代表参数集合
    acc_subset=[]
    xx=np.array(range(5,205,5))*0.01
    for i in tqdm.tqdm(xx):
        
        # 定义进行L1正则化特征选择的模型
        lsvc_l1 = LinearSVC(C=i, penalty="l1", dual=False)
        
        # 交叉验证计算应用特征子集的平均准确率
        scores=cross_validation.cross_val_score(lsvc_l1, train_x, train_y, cv=5)
        acc_subset.append(scores.mean())
    # yy代表不同参数下应用特征子集的平均准确率
    # y0代表应用特征全集的平均准确率，以此作baseline
    yy=acc_subset
    y0=[score.mean()]*len(xx)
    
    # 比较应用特征全集和特征子集的区别
    fig=plt.figure(figsize=(18,6))
    ax1=fig.add_subplot(1,2,1)
    plt.plot(xx,yy,"g-",marker='*')
    plt.plot(xx,y0,"b-")
    ax1.set_xlabel("惩罚系数",fontproperties='SimHei')
    ax1.set_ylabel("交叉验证得到的平均准确率",fontproperties='SimHei')
    ax1.set_title("比较应用特征全集和特征子集的区别",fontproperties='SimHei')
    ax1.set_ylim([score.mean()-0.01,max(yy)+0.01])
    ax1.set_xlim([min(xx),max(xx)])
    
    # 观察不同特征子集的区别
    ax2=fig.add_subplot(1,2,2)
    plt.plot(xx,yy,"g-",marker='*')
    plt.plot(xx,y0,"b-")
    ax2.set_xlabel("惩罚系数",fontproperties='SimHei')
    ax2.set_ylabel("交叉验证得到的平均准确率",fontproperties='SimHei')
    ax2.set_title("不同参数的比较",fontproperties='SimHei')
    ax2.set_ylim([min(yy)-0.001,max(yy)+0.001])
    ax2.set_xlim([min(xx),max(xx)])
    plt.show()


def model(train_x, test_x, train_y, test_y):
    # 建立L1正则化模型
    lsvc_l1 = LinearSVC(C=1.7, penalty="l1", dual=False).fit(train_x, train_y)
    pred=lsvc_l1.predict(test_x)
    
    # 输出经L1正则化选出的特征名称
    model = SelectFromModel(lsvc_l1,prefit=True)
    new_train_x = model.transform(train_x).T
    FS_result=find_name(new_train_x, train_x)
    #accuracy
    acc_subset = metrics.accuracy_score(test_y,pred)
    
    #precision
    precision_subset = metrics.precision_score(test_y,pred,average='weighted')
    
    #recall
    recall_subset = metrics.recall_score(test_y,pred,average='weighted')

    #f1-score
    f1_subset = metrics.f1_score(test_y,pred,average='weighted')
    evaluate_subset = [acc_subset,precision_subset,recall_subset,f1_subset]
    
    evaluate(pred,test_y)
    
    return evaluate_subset

def select_tree(train_x, train_y):
    # 定义以Gini不纯度为分类指标的模型
    clf_gini = ExtraTreesClassifier(criterion='gini')

    # 在训练集上拟合模型，获得特征重要性得分
    clf_gini = clf_gini.fit(train_x, train_y)
    importance_gini=clf_gini.feature_importances_ 
    
    # 交叉验证计算应用特征全集的平均准确率
    score_gini=cross_validation.cross_val_score(clf_gini, train_x, train_y, cv=5)
    
    # 定义以Entropy熵为分类指标的模型
    clf_entropy = ExtraTreesClassifier(criterion='entropy')

    # 在训练集上拟合模型，获得特征重要性得分
    clf_entropy = clf_entropy.fit(train_x, train_y)
    importance_entropy=clf_entropy.feature_importances_
    
    # 交叉验证计算应用特征全集的平均准确率
    score_entropy=cross_validation.cross_val_score(clf_entropy, train_x, train_y, cv=5)
    # 以Gini不纯度为指标
    # 探讨不同特征个数对特征选择效果的影响
    # xx代表特征个数集合
    acc_subset_gini=[]
    xx=np.array(range(1,56,1))
    for i in tqdm.tqdm(xx):
        
        # 定义ExtraTrees模型
        clf_gini = ExtraTreesClassifier(criterion='gini')
        
        # 根据特征重要性选择特征
        feature=FS_importance(importance_gini, train_x.columns, i)
        new_train_x=train_x[feature]
        
        # 交叉验证计算应用特征子集的平均准确率
        scores=cross_validation.cross_val_score(clf_gini, new_train_x, train_y, cv=5)
        acc_subset_gini.append(scores.mean())
        # 以Entropy熵为指标
    # 探讨不同特征个数对特征选择效果的影响
    # xx代表特征个数集合
    acc_subset_entropy=[]
    xx=np.array(range(1,56,1))
    for i in tqdm.tqdm(xx):
        
        # 定义ExtraTrees模型
        clf_entropy = ExtraTreesClassifier(criterion='entropy')
        
        # 根据特征重要性选择特征
        feature=FS_importance(importance_entropy, train_x.columns, i)
        new_train_x=train_x[feature]
        
        # 交叉验证计算应用特征子集的平均准确率
        scores=cross_validation.cross_val_score(clf_entropy, new_train_x, train_y, cv=5)
        acc_subset_entropy.append(scores.mean())
        
    # 以Gini不纯度为指标
    # yy代表不同特征个数下应用特征子集的平均准确率
    # y0代表应用特征全集的平均准确率，以此作baseline
    yy=acc_subset_gini
    y0=[score_gini.mean()]*len(xx)
    
    # 比较应用特征全集和特征子集的区别
    fig=plt.figure(figsize=(18,6))
    ax1=fig.add_subplot(1,2,1)
    plt.plot(xx,yy,"g-",marker='*')
    plt.plot(xx,y0,"b-")
    ax1.set_xlabel("特征个数",fontproperties='SimHei')
    ax1.set_ylabel("交叉验证得到的平均准确率",fontproperties='SimHei')
    ax1.set_title("Gini")
    ax1.set_ylim([min(yy)-0.001,max(yy)+0.001])
    ax1.set_xlim([min(xx),max(xx)])
    
    # yy代表不同参数下应用特征子集的平均准确率
    # y0代表应用特征全集的平均准确率，以此作baseline
    yy=acc_subset_entropy
    y0=[score_entropy.mean()]*len(xx)
    
    # 观察不同特征子集的区别
    ax2=fig.add_subplot(1,2,2)
    plt.plot(xx,yy,"g-",marker='*')
    plt.plot(xx,y0,"b-")
    ax2.set_xlabel("特征个数",fontproperties='SimHei')
    ax2.set_ylabel("交叉验证得到的平均准确率",fontproperties='SimHei')
    ax2.set_title("Entropy")
    ax2.set_ylim([min(yy)-0.001,max(yy)+0.001])
    ax2.set_xlim([min(xx),max(xx)])
    plt.show()
    
    print("最重要的6个特征(gini):")
    print(FS_importance(importance_gini, train_x.columns, 6))
    print("最重要的6个特征(entropy):")
    print(FS_importance(importance_entropy, train_x.columns, 6))
    
    return importance_entropy
    
def model_tree(importance_entropy, train_x, test_x, train_y, test_y):
    # 定义ExtraTrees模型
    clf_entropy = ExtraTreesClassifier(criterion='entropy')
        
    # 根据特征重要性选择特征
    feature=FS_importance(importance_entropy, train_x.columns, 6)
    new_train_x=train_x[feature]
    new_test_x=test_x[feature]
    
    clf_entropy = clf_entropy.fit(new_train_x, train_y) 
    pred=clf_entropy.predict(new_test_x)
    #accuracy
    acc_subset = metrics.accuracy_score(test_y,pred)
    
    #precision
    precision_subset = metrics.precision_score(test_y,pred,average='weighted')
    
    #recall
    recall_subset = metrics.recall_score(test_y,pred,average='weighted')
    
    #f1-score
    f1_subset = metrics.f1_score(test_y,pred,average='weighted')
    evaluate_subset = [acc_subset,precision_subset,recall_subset,f1_subset]
    evaluate(pred,test_y)
    
    return evaluate_subset
if __name__=="__main__":
    df=pd.read_csv("bank-additional-full.csv" , sep=";" , engine = 'python')
    data=df.copy()
    train_x, test_x, train_y, test_y = data_preprocessing(data)
    select(train_x,train_y)
    evaluate_subset = model(train_x, test_x, train_y, test_y)
    importance_entropy = select_tree(train_x, train_y)
    evaluate_subset_tree = model_tree(importance_entropy, train_x, test_x, train_y, test_y)
    

• RFE

  • RFE模型稳定性与对特征评价模型有很大的关系，使用线性回归模型，保留6个特征作为特征子集：‘pdays’,‘previous’,‘emp.var.rate’, ‘cons.price.idx’, ‘cons.conf.idx’, ‘month_mar’。
    
    最终得到模型准确率：
    

def rfe(train_x, test_x, train_y, test_y):
    lr = LinearRegression()
    #保留6个特征
    rfe = RFE(lr,6)          
    #rfe模型拟合
    rfe.fit(train_x,train_y) 
    col = train_x.columns[rfe.support_]
    print(col)
    #筛选出特征子集
    train_x_rfe = train_x[col]    
    lr = LogisticRegression().fit(train_x_rfe,train_y)
    test_x_rfe = test_x[col]
    #模型预测
    pred = lr.predict(test_x_rfe)     
    #准确率
    score = lr.score(test_x_rfe,test_y)
    print("accuracy: ",score)