神经网络的梯度下降公式推导及代码实现

神经网络的梯度下降公式推导及代码实现

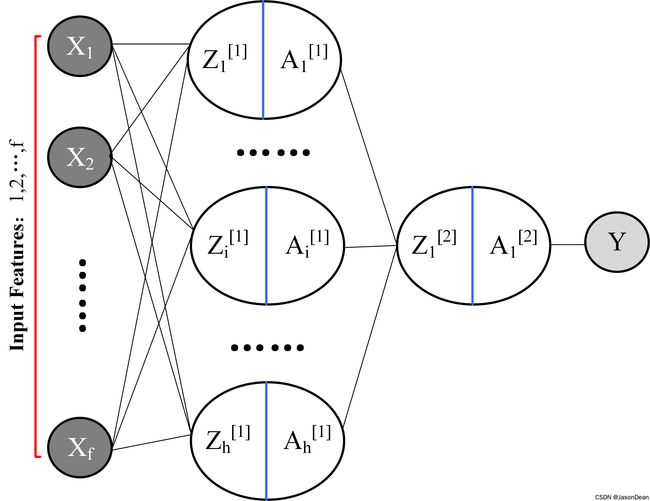
1. 神经网络结构

以 2-Layers-Neural Network 为例，其结构如下。
该神经网络有两层，仅有一层为隐藏层。输入相应的数据$X=\{X_1,X_2,\cdots ,X_f\}$，输出为对应标签 $Y$

神经网络的梯度下降（Gradient descent）更新步骤基本为：

Step 1	Step 2	Step 3	Step 4
Forward Propagation	计算Cost Function	Back Propagation	更新参数W，b

表格描述的是一个epoch的步骤，需要不停的重复Step 1~4, 需经过多个epochs直到Cost Function 收敛

---

2. Step 1: Forward Propagation

其第一层（隐藏层）由 $ h $ 个神经元（隐藏单元）构成, 每个神经元的都要经过两部计算：

1. $Z_1^{[1]}=W_1^{[1]T}X+b^{[1]},X=\{X_1,X_2,\cdots ,X_f{\}}^T$
2. $A_1^{[1]}=\sigma (Z_1^{[1]})=1/(1+exp(-Z_1^{[1]}))$

同理, 只需要改变一下对应的下角标, $Z_2^{[1]}\sim Z_h^{[1]},A_2^{[1]}\sim A_h^{[1]}$ 也能被计算出来。
此时，第一层神经元的输出为 $A^{[1]}=\{A_1^{[1]},A_2^{[1]},\cdots ,A_h^{[1]}\}$
接下来进行下一层的计算：

1. $Z_1^{[2]}=W_1^{[2]T}X+b^{[2]}$
2. $A_1^{[2]}=\sigma (Z_1^{[2]})=1/(1+exp(-Z_1^{[2]}))$

此时，$A_1^{[2]}$ 为模型生成的一个0~1之间的数字,需要利用一定的阈值使得其能变为标签值 $Y\in \{0,1\}$

if {A2 < 0.5}:
    Y = 0 
else：
    Y = 1 

由于第二层只有一个神经元，因此本文中 $Z_1^{[2]} $ 和 $Z^{[2]} $ 代表相同含义

• 简单的描述一下数据集的结构：
  数据集为 $T=\{((X_1^{(i)},X_2^{(i)},\cdots ,X_f^{(i)}),Y^{(i)})\},i=\{1,2,\cdots ,m\}$
  其中，$f$ 为 feature个数，$m$ 为训练集的sample数, $Y \in {0,1} $. 下图举了两个samples的例子. 因此, Forward Propagation 可以简化为：

$$[\begin{array}{rl}{Z}^{[1]}& =W^{[1]}\cdot X+b^{[1]}\\ A^{[1]}& =\sigma \left(Z^{[1]}\right)\\ Z^{[2]}& =W^{[2]}{A}^{[1]}+b^{[2]}\\ A^{[2]}& =\sigma \left(Z^{[2]}\right)\end{array}$$

---

3. Step 2: 计算 Cost Function

Cost Function是对于每一个样本的 Loss 函数的平均值，计算如下：
$$\begin{array}{rl}CostFunction：J(w,b)& =\frac{1}{m}\sum _{i=1}^{m}L\left({\hat{y}}^{(i)},y^{(i)}\right)\\ & =-\frac{1}{m}\sum _{i=1}^m[\left(y^{(i)}\log \left({\hat{y}}^{(i)}\right)+\left(1-y^{(i)}\right)\log \left(1-{\hat{y}}^{(i)}\right)\right]\end{array}$$
其中，${\hat{y}}^{(i)}=A^{[2](i)}$,及第二层第 $i$ 个 sample.

4. Step 3: Back Propagation

Back Propagation 是基于Chain Theory的梯度计算方法。其输出为W，b参数的梯度，以实现参数更新。

梯度下降的参数更新为：
$$W\leftarrow W-\alpha \frac{\partial J(W,b)}{\partial W},b\leftarrow b-\alpha \frac{\partial J(W,b)}{\partial b}$$
$\alpha :learningrate$ 学习率小更新慢，反之则快。
因此，如果要更新 W 和 b，则需要计算对应的梯度。

由Forward Propagation知道，我么们需要计算的梯度由：
$$\frac{\partial J(W,b)}{\partial W^{[2]}},\frac{\partial J(W,b)}{\partial W^{[1]}},\frac{\partial J(W,b)}{\partial b^{[2]}},\frac{\partial J(W,b)}{\partial b^{[1]}}$$
则其计算如下：

4.1 梯度 $\frac{\partial J(W,b)}{\partial W^{[2]}}$ 的计算

$$\frac{\partial J(W,b)}{\partial W^{[2]}}=\frac{dJ}{d{Z}^{[2]}}\frac{d{Z}^{[2]}}{d{W}^{[2]}}$$
其中后面一项可以直接求解：
因为$$Z^{[2]}=W^{[2]}{A}^{[1]}+b^{[2]}$$
所以 $$\frac{d{Z}^{[2]}}{d{W}^{[2]}}=\frac{1}{m}{A}^{[1]T}$$
因此只需要求 $\frac{dJ}{d{Z}^{[2]}}$.利用 Chain Theory 可得：
$$\frac{dJ}{d{Z}^{[2]}}=\frac{dJ}{d{A}^{[2]}}\frac{d{A}^{[2]}}{d{Z}^{[2]}}=A^{[2]}-Y$$
则$$\frac{\partial J(W,b)}{\partial W^{[2]}}=(A^{[2]}-Y)\times \frac{1}{m}{A}^{[1]T}$$

推导1: 求证下面等式 $$\frac{d{Z}^{[2]}}{d{W}^{[2]}}=\frac{1}{m}{A}^{[1]T}$$

• 如何理解 $\frac{d{Z}^{[2]}}{d{W}^{[2]}}$ 的维度问题？
  $$Z^{[2]}=W^{[2]}{A}^{[1]}+b^{[2]}$$
  其中 $A^{[1]}\in {\mathbb{R}}^{h\times m}$, $Z^{[2]}\in {\mathbb{R}}^{1\times m}$
  , $W^{[2]}\in {\mathbb{R}}^{1\times h}$, $b^{[2]}\in {\mathbb{R}}^{1\times m}$.
  拿出 $Z^{[2]}$ 和 $W^{[2]}$ 具体分析：
  $$Z^{[2]}=\{Z^{[2](1)},Z^{[2](2)},Z^{[2](3)},\cdots ,Z^{[2](m)}{\}}_{1\times m}$$
  $$A^{[1]}={\left[\begin{array}{cccc}\mid & \mid & \mid & \mid \\ a^{[1](1)}& a^{[1](2)}& \cdots & a^{[1](m)}\\ \mid & \mid & \mid & \mid \end{array}\right]}_{h\times m}$$
  $$W^{[2]}=\{W_1^{[2]},W_2^{[2]},W_3^{[2]},\cdots ,W_h^{[2]}{\}}_{1\times h}$$
  则 $$\begin{array}{rl}{Z}^{[2]}& =\{Z^{[2](1)},Z^{[2](2)},Z^{[2](3)},\cdots ,Z^{[2](m)}{\}}_{1\times m}\\ & =\{W_1^{[2]},W_2^{[2]},W_3^{[2]},\cdots ,W_h^{[2]}\}\times {\left[\begin{array}{cccc}\mid & \mid & \mid & \mid \\ a^{[1](1)}& a^{[1](2)}& \cdots & a^{[1](m)}\\ \mid & \mid & \mid & \mid \end{array}\right]}_{h\times m}\end{array}$$
  因为：$\frac{d{Z}^{[2]}}{d{W}^{[2]}}$则表示：
  $$\{d{Z}^{[2]}{\}}_{m\times 1}^T=\frac{d{Z}^{[2]}}{d{W}^{[2]}}\{d{W}^{[2]}{\}}_{h\times 1}^T$$
  则 $\frac{d{Z}^{[2]}}{d{W}^{[2]}}$ 维度为 (m,h)
  $$\left[\begin{array}{c}d{Z}^{[2](1)}\\ d{Z}^{[2](2)}\\ d{Z}^{[2](3)}\\ ⋮\\ d{Z}^{[2](m)}\end{array}\right]=\frac{1}{m}{\left[\begin{array}{cccc}\frac{d{Z}^{[2](1)}}{d{W}_1^{[2]}}& \frac{d{Z}^{[2](1)}}{d{W}_2^{[2]}}& \cdots & \frac{d{Z}^{[2](1)}}{d{W}_h^{[2]}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{d{Z}^{[2](m)}}{d{W}_1^{[2]}}& \frac{d{Z}^{[2](m)}}{d{W}_2^{[2]}}& \cdots & \frac{d{Z}^{[2](m)}}{d{W}_h^{[2]}}\end{array}\right]}_{m\times h}\times \left[\begin{array}{c}d{W}_1^{[2]}\\ d{W}_2^{[2]}\\ d{W}_3^{[2]}\\ ⋮\\ d{W}_h^{[2]}\end{array}\right]=\frac{1}{m}{A}^{[1]T}\times \left[\begin{array}{c}d{W}_1^{[2]}\\ d{W}_2^{[2]}\\ d{W}_3^{[2]}\\ ⋮\\ d{W}_h^{[2]}\end{array}\right]$$
  因此，可以推导出 $$\frac{d{Z}^{[2]}}{d{W}^{[2]}}=\frac{1}{m}{A}^{[1]T}$$

4.1 梯度 $\frac{\partial J(W,b)}{\partial b^{[2]}}$ 的计算

$$\frac{\partial J(W,b)}{\partial b^{[2]}}=\frac{dJ}{d{Z}^{[2]}}\frac{d{Z}^{[2]}}{d{b}^{[2]}}=(A^{[2]}-Y{)}_{1\times m}\times \{1{\}}_{m\times 1}\times \frac{1}{m}$$
这相当于是对$(A^{[2]}-Y{)}_{1\times m}$求平均值。

import numpy as np

dZ2 = A2 - Y
db2 = 1.0 / m * np.sum(dZ2, axis=1, keepdims=True)

4.2 梯度 $\frac{\partial J(W,b)}{\partial b^{[1]}}$ $\frac{\partial J(W,b)}{\partial W^{[1]}}$ 的计算

其他梯度也可以通过类似的方式求解
$$\begin{gathered} \frac{\partial J(W,b)}{\partial W^{[1]}}=\frac{dJ}{d{Z}^{[1]}}{X}^T \\ \frac{\partial J(W,b)}{\partial b^{[1]}}=\frac{dJ}{d{Z}^{[1]}} \\ \frac{dJ}{d{Z}^{[1]}}=W^{[2]}\frac{dJ}{d{Z}^{[2]}}\ast {\sigma }^{[1{]}^{\prime }}(Z^{[1]}) \end{gathered}$$

5. 参数更新

梯度下降的参数更新为：
$$\begin{gathered} W^{[1]}\leftarrow W^{[1]}-\alpha \frac{\partial J{(}^{[1]},b^{[1]})}{{\partial }^{[1]}},b^{[1]}\leftarrow b^{[1]}-\alpha \frac{\partial J(W^{[1]},b^{[1]})}{\partial b^{[1]}} \\ {W}^{[2]}\leftarrow W^{[2]}-\alpha \frac{\partial J{(}^{[2]},b^{[2]})}{{\partial }^{[2]}},b^{[2]}\leftarrow b^{[2]}-\alpha \frac{\partial J(W^{[2]},b^{[2]})}{\partial b^{[2]}} \end{gathered}$$
$\alpha :learningrate$ 学习率小更新慢，反之则快。

6. 部分函数以及代码实现

详情可见 Coursera Deep Learning.

def forward_propagation(X, parameters):
    """
    Argument:
    X -- input data of size (n_x, m)
    parameters -- python dictionary containing your parameters (output of initialization function)

    Returns:
    A2 -- The sigmoid output of the second activation
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
    """
    # Retrieve each parameter from the dictionary "parameters"

    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    # Implement Forward Propagation to calculate A2 (probabilities)

    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)

    assert (A2.shape == (1, X.shape[1]))

    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}

    return A2, cache


def compute_cost(A2, Y):
    """
    Computes the cross-entropy cost given in equation (13)

    Arguments:
    A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)
    parameters -- python dictionary containing your parameters W1, b1, W2 and b2

    Returns:
    cost -- cross-entropy cost given equation (13)
    """

    m = Y.shape[1]  # number of example

    # Compute the cross-entropy cost

    logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1 - A2), (1 - Y))
    cost = -(1.0 / m) * np.sum(logprobs)

    cost = np.squeeze(cost)  # makes sure cost is the dimension we expect. # E.g., turns [[17]] into 17

    assert (isinstance(cost, float))

    return cost

    
def backward_propagation(parameters, cache, X, Y):
    """
    Implement the backward propagation using the instructions above.

    Arguments:
    parameters -- python dictionary containing our parameters
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
    X -- input data of shape (2, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)

    Returns:
    grads -- python dictionary containing your gradients with respect to different parameters
    """
    m = X.shape[1]  # sample size

    # First, retrieve W1 and W2 from the dictionary "parameters".

    W1 = parameters["W1"]
    W2 = parameters["W2"]

    # Retrieve also A1 and A2 from dictionary "cache".

    A1 = cache["A1"]
    A2 = cache["A2"]

    # Backward propagation: calculate dW1, db1, dW2, db2.

    dZ2 = A2 - Y
    dW2 = 1.0 / m * np.dot(dZ2, A1.T)
    db2 = 1.0 / m * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
    dW1 = 1.0 / m * np.dot(dZ1, X.T)
    db1 = 1.0 / m * np.sum(dZ1, axis=1, keepdims=True)

    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}

    return grads
def update_parameters(parameters, grads, learning_rate=1.2):
    """
    Updates parameters using the gradient descent update rule given above

    Arguments:
    parameters -- python dictionary containing your parameters
    grads -- python dictionary containing your gradients

    Returns:
    parameters -- python dictionary containing your updated parameters
    """
    # Retrieve each parameter from the dictionary "parameters"

    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    # Retrieve each gradient from the dictionary "grads"

    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]

    # Update rule for each parameter

    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters


def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
    """
    Arguments:
    X -- dataset of shape (2, number of examples)
    Y -- labels of shape (1, number of examples)
    n_h -- size of the hidden layer
    num_iterations -- Number of iterations in gradient descent loop
    print_cost -- if True, print the cost every 1000 iterations

    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]

    # Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2,
    # parameters".

    parameters = initialize_parameters(n_x, n_h, n_y)
    # W1 = parameters["W1"]
    # b1 = parameters["b1"]
    # W2 = parameters["W2"]
    # b2 = parameters["b2"]

    # Loop (gradient descent)
    Cost_plot = []
    for i in range(0, num_iterations):

        # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
        A2, cache = forward_propagation(X, parameters)

        # Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
        cost = compute_cost(A2, Y)

        # Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
        grads = backward_propagation(parameters, cache, X, Y)

        # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
        parameters = update_parameters(parameters, grads, learning_rate=1.2)

        # Stack all the cost for plot

        Cost_plot = np.append(Cost_plot, cost)
        # Print the cost every 1000 iterations
        if print_cost and i % 10 == 0:
            print("Cost after iteration %i: %f" % (i, cost))

    return parameters, Cost_plot

def predict(parameters, X):
    """
    Using the learned parameters, predicts a class for each example in X

    Arguments:
    parameters -- python dictionary containing your parameters
    X -- input data of size (n_x, m)

    Returns
    predictions -- vector of predictions of our model (red: 0 / blue: 1)
    """

    # Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.

    A2, cache = forward_propagation(X, parameters)
    predictions = (A2 > 0.5)

    return predictions

• Main Process

# Package imports
import numpy as np
import matplotlib.pyplot as plt
import sklearn.linear_model

from NN_Compute_Function import nn_model, predict
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

np.random.seed(1)  # set a seed so that the results are consistent

'''
    Import the data from Datasets
'''
# Visualize the data:
X, Y = load_planar_dataset()

'''
    Build a model with a n_h-dimensional hidden layer
'''
parameters, cost_for_plot = nn_model(X, Y, n_h=9, num_iterations=10000, print_cost=True)

plt.plot(cost_for_plot, label='Cost function')
plt.legend()
plt.show()

# Print accuracy of 2-Layers-NN
predictions = predict(parameters, X)
print('Accuracy of 2-Layers-NN: %d' % float(
    (np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%'
      + " with hidden layer size of " + str(4))

if __name__ == "__main__":
    print('=====[This is implementation of two layers neural network on classification]=====')