NLP-词向量(Word Embedding)-2013:Word2vec模型(CBOW、Skip-Gram)【对NNLM的简化】【层次Softmax、负采样、重采样】【静态表示;无法解决一词多义】
一、文本的表示方法 (Representation)
- 文本是一种非结构化的数据信息,是不可以直接被计算的。因为文本不能够直接被模型计算,所以需要将其转化为向量。
- 文本表示的作用就是将这些非结构化的信息转化为结构化的信息,这样就可以针对文本信息做计算,来完成我们日常所能见到的文本分类,情感判断等任务。
- 独热编码 (one-hot representation)
- 整数编码
- 词嵌入(word embedding)
1、独热编码 (one-hot representation)
- 假如我们要计算的文本中一共出现了4个词:猫、狗、牛、羊。向量里每一个位置都代表一个词。所以用 one-hot 来表示就是:
- 猫:[1,0,0,0]
- 狗:[0,1,0,0]
- 牛:[0,0,1,0]
- 羊:[0,0,0,1]
- 但是在实际情况中,文本中很可能出现成千上万个不同的词,这时候向量就会非常长。其中99%以上都是 0。
在one-hot编码中,每一个token(词汇)使用一个长度为N的向量表示,N表示词典的数量。
one-hot编码又称独热编码,将每个词表示成具有n个元素的向量,这个词向量中只有一个元素是1,其他元素都是0,不同词汇元素为0的位置不同,其中n的大小是整个语料中不同词汇的总数.
即:把待处理的文档进行分词或者是N-gram处理,然后进行去重得到词典,假设我们有一个文档:深度学习,那么进行one-hot处理后的结果如下:
| token | one-hot encoding |
|---|---|
| 深 | 1000 |
| 度 | 0100 |
| 学 | 0010 |
| 习 | 0001 |
手工进行one-hot编码:
from sklearn.externals import joblib # 导入用于对象保存与加载的joblib
from keras.preprocessing.text import Tokenizer # 导入keras中的词汇映射器Tokenizer
vocab = {"周杰伦", "陈奕迅", "王力宏", "李宗盛", "周华健", "鹿晗"} # 假定vocab为语料集所有不同词汇集合
t = Tokenizer(num_words=None, char_level=False) # 实例化一个词汇映射器对象
t.fit_on_texts(vocab) # 使用映射器拟合现有文本数据
for token in vocab:
zero_list = [0]*len(vocab)
token_index = t.texts_to_sequences([token])[0][0] - 1 # 使用映射器转化现有文本数据, 每个词汇对应从1开始的自然数;返回样式如: [[2]], 取出其中的数字需要使用[0][0]
zero_list[token_index] = 1
print(token, "的one-hot编码为:", zero_list)
tokenizer_path = "./Tokenizer" # 使用joblib工具保存映射器, 以便之后使用
joblib.dump(t, tokenizer_path)
打印结果:
鹿晗 的one-hot编码为: [1, 0, 0, 0, 0, 0]
王力宏 的one-hot编码为: [0, 1, 0, 0, 0, 0]
李宗盛 的one-hot编码为: [0, 0, 1, 0, 0, 0]
陈奕迅 的one-hot编码为: [0, 0, 0, 1, 0, 0]
周杰伦 的one-hot编码为: [0, 0, 0, 0, 1, 0]
周华健 的one-hot编码为: [0, 0, 0, 0, 0, 1]
one-hot编码的优劣势:
- 优势:操作简单,容易理解.
- 劣势:完全割裂了词与词之间的联系,而且在大语料集下,每个向量的长度过大,占据大量内存.
正因为one-hot编码明显的劣势,这种编码方式被应用的地方越来越少,取而代之的是稠密向量的表示方法word embedding
2、整数编码
- 这种方式也非常好理解,用一种数字来代表一个词,假如我们要计算的文本中一共出现了4个词:猫、狗、牛、羊。则:
- 猫:1
- 狗:2
- 牛:3
- 羊:4
- 将句子里的每个词拼起来就是可以表示一句话的向量。
- 整数编码的缺点如下:
- 无法表达词语之间的关系
- 对于模型解释而言,整数编码可能具有挑战性。
3、词向量/词嵌入(Word Embedding)
是一种Distributed Representation(分布式的表示方法)

word embedding是深度学习中表示文本常用的一种方法。
别人已经训练好了将token(词汇/符号)转为词向量的模型,可以直接使用已训练好的模型直接将token(词汇/符号)转为vector【迁移学习】。比如fastText的预训练词向量模型。参考:fastText词向量模型迁移(直接拿别人已经训练好的词向量模型来使用)
- 传统的自然语言处理系统把词(word)当作一个离散的原子符号。比如,猫可以使用Id537来表示,Id143表示狗。这些编码是任意的,这些编码对于系统处理不同的单词并没有提供有用的信息。这就意味着,如果系统已经学习了什么是“猫”的信息,但这个系统处理什么是“狗”是并没有提供很大的帮助(比如:他们都是动物,有四条腿,宠物,等)。这种词的表示是独立的,离散的Id使得数据之间并没有很大的关联,通常也意味着我们需要更多的数据去成功的训练统计模型。
- 然而,向量(vector representation)克服了这些缺点。

- Word embedding 是自然语言处理(NLP)中的重要环节,它是一些语言处理模型的统称,并不具体指某种算法或模型。Word embedding 的任务是把词转换成可以计算的向量 。
- 从概念上讲,它涉及从每个单词一维的空间到具有更低维度的连续向量空间的数学嵌入。
- In typical word embedding, each word type has an embedding.
- 不同的token(词汇)如果属于同一个 word type,那么这些不同的token(符号)所对应的vector是一样的。
- 生成这种映射的方法包括神经网络,单词共生矩阵的降维,概率模型,可解释的知识库方法,和术语的显式表示单词出现的上下文。
- 当用作底层输入表示时,单词和短语嵌入已经被证明可以提高NLP任务的性能,例如句法分析和情感分析。
- word embedding 是文本表示的一类方法。跟 one-hot 编码和整数编码的目的一样,不过他有更多的优点。
- 词嵌入(word embedding)并不特指某个具体的算法,跟上面2种方式相比,这种方法有几个明显的优势:
- 把一个词映射到成一个实值向量空间。
- 他可以将文本通过一个低维向量来表达,不像 one-hot 那么长。
- 语意相似的词在向量空间上也会比较相近。
- 通用性很强,可以用在不同的任务中。
- 假如我们要计算的文本中一共出现了4个词:猫、狗、牛、羊。则:
- 词嵌入(Word Embedding)的分类
- 基于频率的 Word Embedding(Frequency-Based Word Embedding)
- 基于预测的 Word Embedding(Predict-Based Word Embedding)
4、句子向量(Sentence Embedding)
4.1 Average 法则
句子向量=所含词向量的平均值
4.2 LSTM/RNN
二、基于频率的 Word Embedding【效果不如基于预测的 Word Embedding】
1、count vector(统计词频)
假设语料库中一共有 D D D 个文档,单词库为 V V V, d i m ( V ) = N dim(V) = N dim(V)=N 表示一共有 N N N 个词。则 counter vector就是针对 D D D 个文档,每个文档中各个单词的出现次数。使用统计后的词频组成的向量作为文本句子的Embedding向量,没考虑句子中词汇的顺序以及词汇的重要性程度。
最后的结果是一个 D ∗ N D * N D∗N 大小的矩阵。横坐标的含义是文档编号,纵坐标的含义是单词库的每个词,矩阵的值是代表这个词在这个文档中出现的词频。这个矩阵的size是 D × N D×N D×N。 因为N一般特别的大,有几百万几多,通常的做法是取top10000的词,而忽略其它低频的词。
sklearn.feature_extraction.text.CountVectorizer 的作用:对文本数据进行特征值化。首先将所有文章里的所有的词统计出来,重复的只统计一次。然后对每篇文章,在词的列表里面进行统计每个词出现的次数。注意:单个字母不统计(因为单个单词没有单词分类依据)。
![]()
DictVectorizer语法:
- CountVectorizer(max_df=1.0,min_df=1,…)----实例化,返回词频矩阵
- CountVectorizer.fit_transform(X,y)----X:文本或者包含文本字符串的可迭代对象;返回值:返回sparse矩阵
- CountVectorizer.inverse_transform(X)----X:array数组或者sparse矩阵;返回值:转换之前数据格式
- CountVectorizer.get_feature_names()----返回值:单词列表
文本特征抽取流程:
- 实例化类CountVectorizer
- 调用fit_transform方法输入数据并转换(注意返回格式,利用toarray()进行sparse矩阵转换array数组)
- 中文需要先进行分词,然后再进行特征抽取。
1.1 不带有中文的文本特征抽取
["life is short,i like python","life is too long,i dislike python"]
# 文本特征抽取
from sklearn.feature_extraction.text import CountVectorizer
def countvec():
"""对文本进行特征值化"""
cv = CountVectorizer()
data = cv.fit_transform(["Python: life is short,i like python. it is python.", "life is too long,i dislike python. it is not python."]) # 列表里表示第一篇文章,第二篇文章
print('cv.get_feature_names() = \n', cv.get_feature_names())
print('data = \n', data)
print('data.toarray() = \n', data.toarray())
return None
if __name__ == "__main__":
countvec()
打印结果:
cv.get_feature_names() =
['dislike', 'is', 'it', 'life', 'like', 'long', 'not', 'python', 'short', 'too']
data =
(0, 2) 1
(0, 4) 1
(0, 8) 1
(0, 1) 2
(0, 3) 1
(0, 7) 3
(1, 6) 1
(1, 0) 1
(1, 5) 1
(1, 9) 1
(1, 2) 1
(1, 1) 2
(1, 3) 1
(1, 7) 2
data.toarray() =
[[0 2 1 1 1 0 0 3 1 0]
[1 2 1 1 0 1 1 2 0 1]]
1.2 带有中文的文本特征抽取(不进行分词)
有中文的文本特征抽取,如果不先进行中文分词,则将一段话当做一个词
["你们感觉人生苦短,你 喜欢python java javascript", "人生 漫长,我们 不喜欢python,react"]
# 文本特征抽取
from sklearn.feature_extraction.text import CountVectorizer
def countvec():
"""对文本进行特征值化"""
cv = CountVectorizer()
data = cv.fit_transform(["你们感觉人生苦短,你 喜欢python java javascript", "人生 漫长,我们 不喜欢python,react"]) # 列表里表示第一篇文章,第二篇文章
print('cv.get_feature_names() = \n', cv.get_feature_names())
print('data = \n', data)
print('data.toarray() = \n', data.toarray())
return None
if __name__ == "__main__":
countvec()
打印结果:
cv.get_feature_names() =
['java', 'javascript', 'react', '不喜欢python', '人生', '你们感觉人生苦短', '喜欢python', '我们', '漫长']
data =
(0, 1) 1
(0, 0) 1
(0, 6) 1
(0, 5) 1
(1, 2) 1
(1, 3) 1
(1, 7) 1
(1, 8) 1
(1, 4) 1
data.toarray() =
[[1 1 0 0 0 1 1 0 0]
[0 0 1 1 1 0 0 1 1]]
1.3 使用“jieba”库进行中文分词的文本特征抽取
安装:pip3 install jieba
使用:jieba.cut("我是一个好程序员")
返回值:词语生成器
# 文本特征抽取
from sklearn.feature_extraction.text import CountVectorizer
import jieba
def cutword():
"""中文分词"""
con1 = jieba.cut("今天很残酷,明天更残酷,后天很美好,但绝对大部分是死在明天晚上,所以每个人不要放弃今天。")
con2 = jieba.cut("我们看到的从很远星系来的光是在几百万年之前发出的,这样当我们看到宇宙时,我们是在看它的过去。")
con3 = jieba.cut("如果只用一种方式了解某样事物,你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。")
# 转换成列表
content1 = list(con1)
content2 = list(con2)
content3 = list(con3)
# 把列表转换成字符串
c1 = ' '.join(content1)
c2 = ' '.join(content2)
c3 = ' '.join(content3)
return c1, c2, c3
def hanzivec():
"""中文特征值化"""
c1, c2, c3 = cutword()
print('c1 = \n', c1)
print('c2 = \n', c2)
print('c3 = \n', c3)
cv = CountVectorizer()
data = cv.fit_transform([c1, c2, c3])
print('cv.get_feature_names() = \n', cv.get_feature_names()) # 单个词不统计
print('data.toarray() = \n', data.toarray())
return None
if __name__ == "__main__":
hanzivec()
打印结果:
c1 =
今天 很 残酷 , 明天 更 残酷 , 后天 很 美好 , 但 绝对 大部分 是 死 在 明天 晚上 , 所以 每个 人 不要 放弃 今天 。
c2 =
我们 看到 的 从 很 远 星系 来 的 光是在 几百万年 之前 发出 的 , 这样 当 我们 看到 宇宙 时 , 我们 是 在 看 它 的 过去 。
c3 =
如果 只用 一种 方式 了解 某样 事物 , 你 就 不会 真正 了解 它 。 了解 事物 真正 含义 的 秘密 取决于 如何 将 其 与 我们 所 了解 的 事物 相 联系 。
cv.get_feature_names() =
['一种', '不会', '不要', '之前', '了解', '事物', '今天', '光是在', '几百万年', '发出', '取决于', '只用', '后天', '含义', '大部分', '如何', '如果', '宇宙', '我们', '所以', '放弃', '方式', '明天', '星系', '晚上', '某样', '残酷', '每个', '看到', '真正', '秘密', '绝对', '美好', '联系', '过去', '这样']
data.toarray() =
[[0 0 1 0 0 0 2 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 2 0 1 0 2 1 0 0 0 1 1 0 0 0]
[0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 3 0 0 0 0 1 0 0 0 0 2 0 0 0 0 0 1 1]
[1 1 0 0 4 3 0 0 0 0 1 1 0 1 0 1 1 0 1 0 0 1 0 0 0 1 0 0 0 2 1 0 0 1 0 0]]
2、tf-idf(抽取词语的重要性):sklearn.feature_extraction.text.TfidfVectorizer
count vector 只考虑了词在各个文档中的出现次数,有一个问题就是有的词不光在当前文档中出现的多,在各个文档中出现的都多,比如像 is a of 这种词,所以这里就引入 i d f idf idf 的概念。
tf-idf 这种方法仍然是一个 D × N D×N D×N的矩阵,横坐标的含义是文档编号,只是矩阵里的值不光考虑 term frequency, 还考虑了idf。
sklearn.feature_extraction.text.TfidfVectorizer 计算的方法如下:
- tf:term frequency---->词频(一个词汇在当前文档中的词频)
- idf:inverse document frequency---->逆文档频率=log( 总文档数量 该词出现的文档数量 \frac{总文档数量}{该词出现的文档数量} 该词出现的文档数量总文档数量)
- tf × idf---->该词在该篇文档中的重要性程度
- tf-idf的主要思想是:如果某个词或短语在一篇文章中出现的概率高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。
- tf-idf作用:用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
- tf-idf是分类机器学习算法的重要依据。
- tf-idf方法比count方法更好一些,但是在自然语言处理过程中会使用比tf-idf更好的方法。
2.1 tf-idf算法代码实现
import numpy as np
import pandas as pd
import math
### 1. 定义数据和预处理
docA = "The cat sat on my bed"
docB = "The dog sat on my knees"
bowA = docA.split(" ")
bowB = docB.split(" ")
print('bowA = {0}'.format(bowA))
print('bowB = {0}'.format(bowB))
# 构建词库
wordSet = set(bowA).union(set(bowB))
print('wordSet = {0}'.format(wordSet))
### 2. 进行词数统计
# 用统计字典来保存词出现的次数
wordDictA = dict.fromkeys(wordSet, 0)
wordDictB = dict.fromkeys(wordSet, 0)
# 遍历文档,统计词数
for word in bowA:
wordDictA[word] += 1
for word in bowB:
wordDictB[word] += 1
print('\nwordDataFrame = \n{0}'.format(pd.DataFrame([wordDictA, wordDictB])))
### 3. 计算词频tf=该词在文章A中的词频
def computeTF(wordDict, bow):
# 用一个字典对象记录tf,把所有的词对应在bow文档里的tf都算出来
tfDict = {}
nbowCount = len(bow)
for word, count in wordDict.items():
tfDict[word] = count / nbowCount
return tfDict
### 4. 计算逆文档频率idf=log(总文档数量/该词出现的文档数量)
def computeIDF(wordDictList):
# 用一个字典对象保存idf结果,每个词作为key,初始值为0
idfDict = dict.fromkeys(wordDictList[0], 0)
N = len(wordDictList)
for wordDict in wordDictList:
# 遍历字典中的每个词汇,统计Ni
for word, count in wordDict.items():
if count > 0:
# 先把Ni增加1,存入到idfDict
idfDict[word] += 1
# 已经得到所有词汇i对应的Ni,现在根据公式把它替换成为idf值
for word, ni in idfDict.items():
idfDict[word] = math.log10((N + 1) / (ni + 1))
return idfDict
### 5. 计算TF-IDF
def computeTFIDF(tf, idfs):
tfidf = {}
for word, tfval in tf.items():
tfidf[word] = tfval * idfs[word]
return tfidf
if __name__ == '__main__':
tfA = computeTF(wordDictA, bowA)
tfB = computeTF(wordDictB, bowB)
print('\ntfA = {0}'.format(tfA))
print('tfB = {0}'.format(tfB))
idfs = computeIDF([wordDictA, wordDictB])
print('\nidfs = {0}'.format(idfs))
tfidfA = computeTFIDF(tfA, idfs)
tfidfB = computeTFIDF(tfB, idfs)
print('\ntfidfDataFrame = \n{0}'.format(pd.DataFrame([tfidfA, tfidfB])))
打印结果:
bowA = ['The', 'cat', 'sat', 'on', 'my', 'bed']
bowB = ['The', 'dog', 'sat', 'on', 'my', 'knees']
wordSet = {'The', 'my', 'sat', 'knees', 'cat', 'on', 'bed', 'dog'}
wordDataFrame =
The bed cat dog knees my on sat
0 1 1 1 0 0 1 1 1
1 1 0 0 1 1 1 1 1
tfA = {'The': 0.16666666666666666, 'my': 0.16666666666666666, 'sat': 0.16666666666666666, 'knees': 0.0, 'cat': 0.16666666666666666, 'on': 0.16666666666666666, 'bed': 0.16666666666666666, 'dog': 0.0}
tfB = {'The': 0.16666666666666666, 'my': 0.16666666666666666, 'sat': 0.16666666666666666, 'knees': 0.16666666666666666, 'cat': 0.0, 'on': 0.16666666666666666, 'bed': 0.0, 'dog': 0.16666666666666666}
idfs = {'The': 0.0, 'my': 0.0, 'sat': 0.0, 'knees': 0.17609125905568124, 'cat': 0.17609125905568124, 'on': 0.0, 'bed': 0.17609125905568124, 'dog': 0.17609125905568124}
tfidfDataFrame =
The bed cat dog knees my on sat
0 0.0 0.029349 0.029349 0.000000 0.000000 0.0 0.0 0.0
1 0.0 0.000000 0.000000 0.029349 0.029349 0.0 0.0 0.0
2.2 tf-idf算法案例
# 文本特征抽取(tf-idf方式)
from sklearn.feature_extraction.text import TfidfVectorizer
import jieba
def cutword():
"""中文分词"""
con1 = jieba.cut("今天很残酷,明天更残酷,后天很美好,但绝对大部分是死在明天晚上,所以每个人不要放弃今天。")
con2 = jieba.cut("我们看到的从很远星系来的光是在几百万年之前发出的,这样当我们看到宇宙时,我们是在看它的过去。")
con3 = jieba.cut("如果只用一种方式了解某样事物,你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。")
# 转换成列表
content1 = list(con1)
content2 = list(con2)
content3 = list(con3)
# 把列表转换成字符串
c1 = ' '.join(content1)
c2 = ' '.join(content2)
c3 = ' '.join(content3)
return c1, c2, c3
def tfidfvec():
"""中文特征值化"""
c1, c2, c3 = cutword()
print('c1 = \n', c1)
print('c2 = \n', c2)
print('c3 = \n', c3)
tfidf = TfidfVectorizer()
data = tfidf.fit_transform([c1, c2, c3])
print('tfidf.get_feature_names() = \n', tfidf.get_feature_names())
print('data.toarray() = \n', data.toarray())
return None
if __name__ == "__main__":
tfidfvec()
打印结果:
c1 =
今天 很 残酷 , 明天 更 残酷 , 后天 很 美好 , 但 绝对 大部分 是 死 在 明天 晚上 , 所以 每个 人 不要 放弃 今天 。
c2 =
我们 看到 的 从 很 远 星系 来 的 光是在 几百万年 之前 发出 的 , 这样 当 我们 看到 宇宙 时 , 我们 是 在 看 它 的 过去 。
c3 =
如果 只用 一种 方式 了解 某样 事物 , 你 就 不会 真正 了解 它 。 了解 事物 真正 含义 的 秘密 取决于 如何 将 其 与 我们 所 了解 的 事物 相 联系 。
tfidf.get_feature_names() =
['一种', '不会', '不要', '之前', '了解', '事物', '今天', '光是在', '几百万年', '发出', '取决于', '只用', '后天', '含义', '大部分', '如何', '如果', '宇宙', '我们', '所以', '放弃', '方式', '明天', '星系', '晚上', '某样', '残酷', '每个', '看到', '真正', '秘密', '绝对', '美好', '联系', '过去', '这样']
data.toarray() =
[[0. 0. 0.21821789 0. 0. 0.
0.43643578 0. 0. 0. 0. 0.
0.21821789 0. 0.21821789 0. 0. 0.
0. 0.21821789 0.21821789 0. 0.43643578 0.
0.21821789 0. 0.43643578 0.21821789 0. 0.
0. 0.21821789 0.21821789 0. 0. 0. ]
[0. 0. 0. 0.2410822 0. 0.
0. 0.2410822 0.2410822 0.2410822 0. 0.
0. 0. 0. 0. 0. 0.2410822
0.55004769 0. 0. 0. 0. 0.2410822
0. 0. 0. 0. 0.48216441 0.
0. 0. 0. 0. 0.2410822 0.2410822 ]
[0.15698297 0.15698297 0. 0. 0.62793188 0.47094891
0. 0. 0. 0. 0.15698297 0.15698297
0. 0.15698297 0. 0.15698297 0.15698297 0.
0.1193896 0. 0. 0.15698297 0. 0.
0. 0.15698297 0. 0. 0. 0.31396594
0.15698297 0. 0. 0.15698297 0. 0. ]]
3、BM25算法(tf-idf改进版)
3.1 BM25算法原理
BM25(BM=best matching)是TDIDF的优化版本,首先我们来看看TFIDF是怎么计算的
t f i d f i = t f ∗ i d f = 词 i 的数量 词语总数 ∗ l o g 总文档数 包含词 i 的文档数 tfidf_i = tf*idf = \cfrac{词i的数量}{词语总数}*log\cfrac{总文档数}{包含词i的文档数} tfidfi=tf∗idf=词语总数词i的数量∗log包含词i的文档数总文档数
其中tf称为词频,idf为逆文档频率
那么BM25是如何计算的呢?
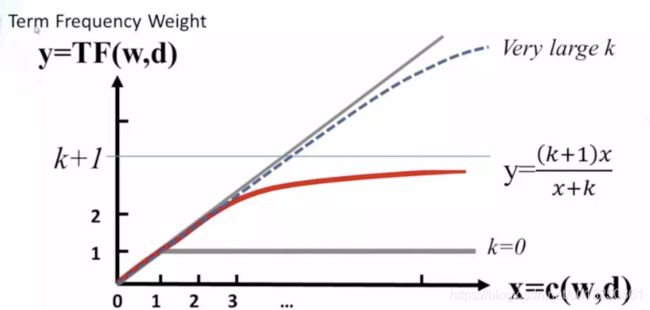
B M 25 ( i ) = 词 i 的数量 总词数 ∗ ( k + 1 ) C C + k ( 1 − b + b ∣ d ∣ a v d l ) ∗ l o g ( 总文档数 包含 i 的文档数 ) C = t f = 词 i 的数量 总词数 , k > 0 , b ∈ [ 0 , 1 ] , d 为文档 i 的长度, a v d l 是文档平均长度 BM25(i) = \cfrac{词i的数量}{总词数}*\cfrac{(k+1)C}{C+k(1-b+b\cfrac{|d|}{avdl})}*log(\cfrac{总文档数}{包含i的文档数}) \\ C = tf=\cfrac{词i的数量}{总词数},k>0,b\in [0,1],d为文档i的长度,avdl是文档平均长度 BM25(i)=总词数词i的数量∗C+k(1−b+bavdl∣d∣)(k+1)C∗log(包含i的文档数总文档数)C=tf=总词数词i的数量,k>0,b∈[0,1],d为文档i的长度,avdl是文档平均长度
大家可以看到,BM25和tfidf的计算结果很相似,唯一的区别在于中多了一项,这一项是用来对tf的结果进行的一种变换。
把 1 − b + b d a v d l 1-b+b\cfrac{d}{avdl} 1−b+bavdld中的b看成0,那么此时中间项的结果为 ( k + 1 ) t f k + t f \cfrac{(k+1)tf}{k+tf} k+tf(k+1)tf,通过设置一个k,就能够保证其最大值为 1 1 1,达到限制tf过大的目的。
即:
( k + 1 ) t f k + t f = k + 1 1 + k t f , 上下同除 t f \begin{aligned} &\cfrac{(k+1)tf}{k+tf}= \cfrac{k+1}{1+\cfrac{k}{tf}} \qquad \qquad \qquad,上下同除tf \end{aligned} k+tf(k+1)tf=1+tfkk+1,上下同除tf
k不变的情况下,上式随着tf的增大而增大,上限为k+1,但是增加的程度会变小,如下图所示。
在一个句子中,某个词重要程度应该是随着词语的数量逐渐衰减的,所以中间项对词频进行了惩罚,随着次数的增加,影响程度的增加会越来越小。通过设置k值,能够保证其最大值为k+1,k往往取值1.2。
其变化如下图(无论k为多少,中间项的变化程度会随着次数的增加,越来越小):
同时 1 − b + b d a v d l 1-b+b\cfrac{d}{avdl} 1−b+bavdld的作用是用来对文本的长度进行归一化。
例如在考虑整个句子的tdidf的时候,如果句子的长度太短,那么计算的总的tdidf的值是要比长句子的tdidf的值要低的。所以可以考虑对句子的长度进行归一化处理。
可以看到,当句子的长度越短, 1 − b + b ∣ d ∣ a v d l 1-b+b\cfrac{|d|}{avdl} 1−b+bavdl∣d∣的值是越小,作为分母的位置,会让整个第二项越大,从而达到提高短文本句子的BM25的值的效果。当b的值为0,可以禁用归一化,b往往取值0.75
其变化效果如下:
3.2 BM25算法实现
通过前面的学习,我们知道其实BM25和Tfidf的区别不大,所以我们可以在之前sciket-learn的TfidfVectorizer基础上进行修改,获取我们的BM25的计算结果,主要也是修改其中的fit方法和transform方法
在sklearn的TfidfVectorizer中,首先接受参数,其次会调用TfidfTransformer来完成其他方法的调用
3.2.1 继承TfidfVectorizer完成 参数的接受
from sklearn.feature_extraction.text import TfidfVectorizer,TfidfTransformer,_document_frequency
from sklearn.base import BaseEstimator,TransformerMixin
from sklearn.preprocessing import normalize
from sklearn.utils.validation import check_is_fitted
import numpy as np
import scipy.sparse as sp
class Bm25Vectorizer(CountVectorizer):
def __init__(self,k=1.2,b=0.75, norm="l2", use_idf=True, smooth_idf=True,sublinear_tf=False,*args,**kwargs):
super(Bm25Vectorizer,self).__init__(*args,**kwargs)
self._tfidf = Bm25Transformer(k=k,b=b,norm=norm, use_idf=use_idf,
smooth_idf=smooth_idf,
sublinear_tf=sublinear_tf)
@property
def k(self):
return self._tfidf.k
@k.setter
def k(self, value):
self._tfidf.k = value
@property
def b(self):
return self._tfidf.b
@b.setter
def b(self, value):
self._tfidf.b = value
def fit(self, raw_documents, y=None):
"""Learn vocabulary and idf from training set.
"""
X = super(Bm25Vectorizer, self).fit_transform(raw_documents)
self._tfidf.fit(X)
return self
def fit_transform(self, raw_documents, y=None):
"""Learn vocabulary and idf, return term-document matrix.
"""
X = super(Bm25Vectorizer, self).fit_transform(raw_documents)
self._tfidf.fit(X)
return self._tfidf.transform(X, copy=False)
def transform(self, raw_documents, copy=True):
"""Transform documents to document-term matrix.
"""
check_is_fitted(self, '_tfidf', 'The tfidf vector is not fitted')
X = super(Bm25Vectorizer, self).transform(raw_documents)
return self._tfidf.transform(X, copy=False)
3.2.2 完成自己的Bm25transformer,只需要再原来基础的代码上进心修改部分即可。sklearn中的转换器类的实现要求,不能直接继承已有的转换器类
class Bm25Transformer(BaseEstimator, TransformerMixin):
def __init__(self,k=1.2,b=0.75, norm='l2', use_idf=True, smooth_idf=True,
sublinear_tf=False):
self.k = k
self.b = b
##################以下是TFIDFtransform代码##########################
self.norm = norm
self.use_idf = use_idf
self.smooth_idf = smooth_idf
self.sublinear_tf = sublinear_tf
def fit(self, X, y=None):
"""Learn the idf vector (global term weights)
Parameters
----------
X : sparse matrix, [n_samples, n_features]
a matrix of term/token counts
"""
_X = X.toarray()
self.avdl = _X.sum()/_X.shape[0] #句子的平均长度
# print("原来的fit的数据:\n",X)
#计算每个词语的tf的值
self.tf = _X.sum(0)/_X.sum() #[M] #M表示总词语的数量
self.tf = self.tf.reshape([1,self.tf.shape[0]]) #[1,M]
# print("tf\n",self.tf)
##################以下是TFIDFtransform代码##########################
if not sp.issparse(X):
X = sp.csc_matrix(X)
if self.use_idf:
n_samples, n_features = X.shape
df = _document_frequency(X)
# perform idf smoothing if required
df += int(self.smooth_idf)
n_samples += int(self.smooth_idf)
# log+1 instead of log makes sure terms with zero idf don't get
# suppressed entirely.
idf = np.log(float(n_samples) / df) + 1.0
self._idf_diag = sp.spdiags(idf, diags=0, m=n_features,
n=n_features, format='csr')
return self
def transform(self, X, copy=True):
"""Transform a count matrix to a tf or tf-idf representation
Parameters
----------
X : sparse matrix, [n_samples, n_features]
a matrix of term/token counts
copy : boolean, default True
Whether to copy X and operate on the copy or perform in-place
operations.
Returns
-------
vectors : sparse matrix, [n_samples, n_features]
"""
########### 计算中间项 ###############
cur_tf = np.multiply(self.tf, X.toarray()) #[N,M] #N表示数据的条数,M表示总词语的数量
norm_lenght = 1 - self.b + self.b*(X.toarray().sum(-1)/self.avdl) #[N] #N表示数据的条数
norm_lenght = norm_lenght.reshape([norm_lenght.shape[0],1]) #[N,1]
middle_part = (self.k+1)*cur_tf /(cur_tf +self.k*norm_lenght)
############# 结算结束 ################
if hasattr(X, 'dtype') and np.issubdtype(X.dtype, np.floating):
# preserve float family dtype
X = sp.csr_matrix(X, copy=copy)
else:
# convert counts or binary occurrences to floats
X = sp.csr_matrix(X, dtype=np.float64, copy=copy)
n_samples, n_features = X.shape
if self.sublinear_tf:
np.log(X.data, X.data)
X.data += 1
if self.use_idf:
check_is_fitted(self, '_idf_diag', 'idf vector is not fitted')
expected_n_features = self._idf_diag.shape[0]
if n_features != expected_n_features:
raise ValueError("Input has n_features=%d while the model"
" has been trained with n_features=%d" % (
n_features, expected_n_features))
# *= doesn't work
X = X * self._idf_diag
############# 中间项和结果相乘 ############
X = X.toarray()*middle_part
if not sp.issparse(X):
X = sp.csr_matrix(X, dtype=np.float64)
############# #########
if self.norm:
X = normalize(X, norm=self.norm, copy=False)
return X
@property
def idf_(self):
##################以下是TFIDFtransform代码##########################
# if _idf_diag is not set, this will raise an attribute error,
# which means hasattr(self, "idf_") is False
return np.ravel(self._idf_diag.sum(axis=0))
完整代码参考:https://github.com/SpringMagnolia/Bm25Vectorzier/blob/master/BM25Vectorizer.py
3.2.3 测试简单使用,观察和tdidf的区别:
from BM25Vectorizer import Bm25Vectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
if __name__ == '__main__':
# format_weibo(word=False)
# format_xiaohuangji_corpus(word=True)
bm_vec = Bm25Vectorizer()
tf_vec = TfidfVectorizer()
# 1. 原始数据
data = [
'hello world',
'oh hello there',
'Play it',
'Play it again Sam,24343,123',
]
# 2. 原始数据向量化
bm_vec.fit(data)
tf_vec.fit(data)
features_vec_bm = bm_vec.transform(data)
features_vec_tf = tf_vec.transform(data)
print("Bm25 result:",features_vec_bm.toarray())
print("*"*100)
print("Tfidf result:",features_vec_tf.toarray())
输出如下:
Bm25 result: [[0. 0. 0. 0.47878333 0. 0.
0. 0. 0. 0.8779331 ]
[0. 0. 0. 0.35073401 0. 0.66218791
0. 0. 0.66218791 0. ]
[0. 0. 0. 0. 0.70710678 0.
0.70710678 0. 0. 0. ]
[0.47038081 0.47038081 0.47038081 0. 0.23975776 0.
0.23975776 0.47038081 0. 0. ]]
**********************************************************************************
Tfidf result: [[0. 0. 0. 0.6191303 0. 0.
0. 0. 0. 0.78528828]
[0. 0. 0. 0.48693426 0. 0.61761437
0. 0. 0.61761437 0. ]
[0. 0. 0. 0. 0.70710678 0.
0.70710678 0. 0. 0. ]
[0.43671931 0.43671931 0.43671931 0. 0.34431452 0.
0.34431452 0.43671931 0. 0. ]]
4、基于共现(Co-Occurence)的Word Embedding方法
- 在统计语言模型中,有一种假设,认为词的语义是由它的上下文所决定的,所以统计当前词的上下文的分布也是一种方式,即统计与当前词共现的词的分布情况。这样建立出来的矩阵的size就是 N × N N×N N×N。 横坐标是每一个词,纵坐标也每一个词,矩阵中每一个点的(word1, word2)的value是指 word2是word1的上下文中出现的次数。
- 词共现矩阵
- 由于共现矩阵保存了词的上下文信息,所以就保存了语义,效果会比之前的好很多。但这种矩阵大小也存在太大的问题,一般的办法是用矩阵分解的方式进行降维。
- 缺点:在词对推理任务上表现特别差;可解释性差;
三、基于预测的 Word Embedding
和one-hot编码不同,word embedding使用了浮点型的稠密矩阵来表示token。根据词典的大小,我们的向量通常使用不同的维度,例如100,256,300等。其中向量中的每一个值是一个参数,其初始值是随机生成的,之后会在训练的过程中进行学习而获得。
如果我们文本中有20000个词语,如果使用one-hot编码,那么我们会有20000*20000的矩阵,其中大多数的位置都为0,但是如果我们使用word embedding来表示的话,只需要20000* 维度,比如20000*300
形象的表示就是:
| token | num | vector |
|---|---|---|
| 词1 | 0 | [ w 11 , w 12 , w 13 . . . w 1 N ] [w_{11},w_{12},w_{13}...w_{1N}] [w11,w12,w13...w1N] ,其中 N N N 表示维度(dimension) |
| 词2 | 1 | [ w 21 , w 22 , w 23 . . . w 2 N ] [w_{21},w_{22},w_{23}...w_{2N}] [w21,w22,w23...w2N] |
| 词3 | 2 | [ w 31 , w 23 , w 33 . . . w 3 N ] [w_{31},w_{23},w_{33}...w_{3N}] [w31,w23,w33...w3N] |
| … | …. | … |
| 词m | m | [ w m 1 , w m 2 , w m 3 . . . w m N ] [w_{m1},w_{m2},w_{m3}...w_{mN}] [wm1,wm2,wm3...wmN],其中 m m m 表示词典的大小 |
我们会把所有的文本转化为向量,把句子用向量来表示
但是在这中间,我们会先把token使用数字来表示,再把数字使用向量来表示。
Embedding Layer(文本嵌入层)的作用:无论是源文本嵌入还是目标文本嵌入,都是为了将文本中词汇的数字表示转变为向量表示, 由一维转为多维,希望在高维空间捕捉词汇间的关系.
- 文本中的单词在输入到文本嵌入层之前,已经通过word2index操作转换为数值【每个单词用该单词在所在词汇表中的序号表示】,将字符串形式的单词转为序号形式,然后输入到文本嵌入层。
- 再通过文本嵌入层将每个单词的一维的数值型序号转为多维向量。
1、word embedding API
torch.nn.Embedding(num_embeddings,embedding_dim)
参数介绍:
num_embeddings:词典的大小embedding_dim:embedding的维度
使用方法:
embedding = nn.Embedding(vocab_size,300) #实例化
input_embeded = embedding(input) #进行embedding的操作
2、数据的形状变化
思考:每个batch中的每个句子有10个词语(即:输入形状为[batch_size,10]),经过[num_embeddings,embedding_dim]的形状为[20,4]的Word emebedding之后,原来的句子会变成什么形状?
每个词语用长度为4的向量表示,所以,最终句子会变为[batch_size,10,4]的形状。
增加了一个维度,这个维度是embedding的dim
3、代码
import torch # 导入必备的工具包
import torch.nn as nn # 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层【比如,卷积层, lstm层, embedding层等, 不需要我们再重新造轮子】
import math # 数学计算工具包
# 定义Embeddings类来实现文本嵌入层,这里s说明代表两个一模一样的嵌入层, 他们共享参数【该类继承nn.Module, 这样就有标准层的一些功能, 这里我们也可以理解为一种模式, 我们自己实现的所有层都会这样去写】
class Embeddings(nn.Module):
# 类的初始化函数, 有两个参数, 【vocab_input_size: 指词表的大小; word_embedding_size: 指转换后的词嵌入的维度】
def __init__(self, vocab_input_size, word_embedding_size):
super(Embeddings, self).__init__() # 使用super的方式指明继承nn.Module的初始化函数, 我们自己实现的所有层都会这样去写.
self.vocab_input_size = vocab_input_size
self.word_embedding_size = word_embedding_size
self.embedding = nn.Embedding(num_embeddings=vocab_input_size, embedding_dim=word_embedding_size) # 调用nn中的预定义层Embedding, 获得一个词嵌入对象self.embedding【vocab_input_size表示词汇表所有单词数量】
# 前向传播逻辑,所有层中都会有此函数,当传给该类的实例化对象参数时, 自动调用该类函数【参数input: 代表单词文本通过词汇映射(word2index)后的数值型张量,input里的每一个数字必须为0~vocab_input_size间的数来代表词汇表里的一个特定单词】
def forward(self, input):
# 将张量input传给self.embedding 返回词向量【math.sqrt(self.word_embedding_size)具有缩放的作用,控制转换后每一个元素的数值大小尽可能离散】
return self.embedding(input) * math.sqrt(self.word_embedding_size)
if __name__ == "__main__":
embedding01 = nn.Embedding(10, 3)
# 输入 input01 形状是 torch.Size([2, 4]),output01 中的每一个数字代表一个单词,该数字必须处于0~10, 通过embedding将每一个数字从一维转为三维
input01 = torch.LongTensor([[1, 2, 4, 5], [4, 3, 2, 9]]) # 其中所有元素的数值必须在0~10之间,1、2、4、5、4、3、2、9 代表在词汇表(该词汇表中的单词总数为10)中的序号分别为1、2、4、5、4、3、2、9的单词
output01 = embedding01(input01)
print("input01.shape = {0}\ninput01 = {1}\noutput01.shape = {2}\noutput01 = {3}".format(input01.shape, input01, output01.shape, output01))
print("=" * 200)
# 输入 input02 形状是 torch.Size([2]),input02 中的每一个数字代表一个单词,该数字必须处于0~125, 通过embedding将每一个数字从一维转为四维
embedding02 = nn.Embedding(125, 4, padding_idx=0)
input02 = torch.LongTensor([99, 20]) # 其中所有元素的数值必须在0~125之间,99、20代表在词汇表(该词汇表中的单词总数为125)中的序号分别为99、20的单词
output02 = embedding02(input02)
print("input02.shape = {0}\ninput02 = {1}\noutput02.shape = {2}\noutput02 = {3}".format(input02.shape, input02, output02.shape, output02))
print("=" * 200)
# 输入 input03 维度为 torch.Size([1]),input03 中的每一个数字代表一个单词,该数字必须处于0~21356, 通过embedding将每一个数字从一维转为七维
embedding03 = nn.Embedding(21356, 7, padding_idx=0)
input03 = torch.LongTensor([12929]) # 其中所有元素的数值必须在0~21356之间,12929代表在词汇表(该词汇表中的单词总数为21356)中的序号为12929的单词
output03 = embedding03(input03)
print("input03.shape = {0}\ninput03 = {1}\noutput03.shape = {2}\noutput03 = {3}".format(input03.shape, input03, output03.shape, output03))
print("=" * 200)
打印结果:
input01.shape = torch.Size([2, 4])
input01 = tensor(
[
[1, 2, 4, 5],
[4, 3, 2, 9]
]
)
output01.shape = torch.Size([2, 4, 3])
output01 = tensor(
[
[[ 0.5935, 0.7198, -0.6062],[ 1.2770, 1.1744, 1.7957],[ 1.6661, -0.1799, 1.3263],[-0.6745, -0.3617, 1.1253]],
[[ 1.6661, -0.1799, 1.3263],[ 0.1904, -1.5195, 1.7049],[ 1.2770, 1.1744, 1.7957],[-1.8913, -1.6058, -0.8754]]
]
, grad_fn=<EmbeddingBackward>)
========================================================================================================================================================================================================
input02.shape = torch.Size([2])
input02 = tensor([99, 20])
output02.shape = torch.Size([2, 4])
output02 = tensor([[-0.9908, 0.7808, -0.5484, 1.2730], [ 1.1635, 0.6166, 0.7226, 0.2980]], grad_fn=<EmbeddingBackward>)
========================================================================================================================================================================================================
input03.shape = torch.Size([1])
input03 = tensor([929])
output03.shape = torch.Size([1, 7])
output03 = tensor([[-2.6139, -0.1027, -1.2199, 0.5283, -0.5732, -0.8206, -1.1798]], grad_fn=<EmbeddingBackward>)
========================================================================================================================================================================================================
Process finished with exit code 0
四、Word2vec语言模型的发展
- 在Word Embedding中只有利用了上下文信息才算进入了language model的范畴。
- 基于共现(Co-Occurence)的矩阵利用了上下文的信息,但是缺点是矩阵太大,一个词的表示要用所有其它的词来表示,会给后述的计算带来各种各样的问题。
- 所以我们需要找到一种更好的word embedding的方法,它需要满足两个条件:
- 携带上下文信息。
- 词的表示是稠密的,维度不要太高。
- 神经网络的出现地为了这个问题提供了很好的解决方案。
- 神经网络最早出现是为了有监督学习服务的,在有监督的学习过程中,可以产出各个词对应的向量。这时候word embedding是神经网络训练的副产品。这时候就出现了一个问题,如何能够无监督地学习各个词的embedding。说了无监督,神经网络的训练肯定是要有输出和label的。而语言模型建模的目标是两个
- 刻划词的上下文。
- 刻划词与词的上下文的关系。
- 第一个问题刻划上下文在NN中比较简单的,直接把上下文作为输入放到NN中就可以。
- 那么第二个问题,如何表示词与词的上下文的关系,这个就比较简单了,直接把当词作为NN的label, 把词的上下文作为NN的输入,输出就是预测出现这个词的概率。
- 实际是最终就是两个步骤:
- 用上下文和词,一个作输入,一个作输出。
- 用NN(神经网络)去刻划他们两者之间的关系。
1、前馈神经网络语言模型(NNLM)【使用马尔科夫假设】【Word2vec的对比模型01】
![]()
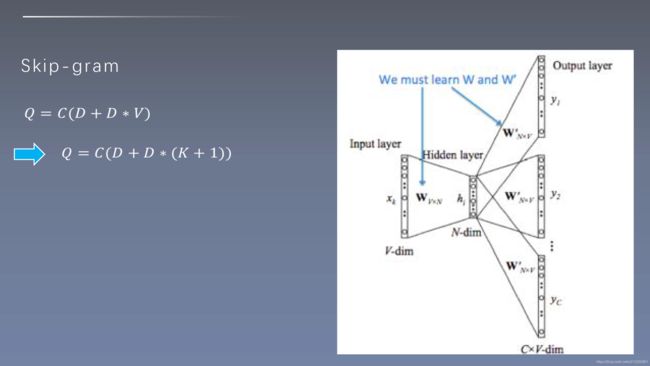
It consists of input, projection, hidden and output layers. At the input layer, N previous words are encoded using 1-of-V coding【N×V】, where V is size of the vocabulary. The input layer is then projected to a projection layer P that has dimensionality N x D【[N×V]·[V×D]==>[N×D]】, using a shared projection matrix【shape=[V×D]】. As only N inputs are active at any given time, composition of the projection layer is a relatively cheap operation.
The NNLM architecture becomes complex for computation between the projection and the hidden layer, as values in the projection layer are dense. For a common choice of N = 10, the size of the projection layer (P)might be 500 to 2000, while the hidden layer size H is typically 500 to 1000 units. Moreover, the hidden layer is used to compute probability distribution over all the words in the vocabulary, resulting in an output layer with dimensionality V . Thus, the computational complexity per each training example is
Q = N × D + N × D × H + H × V , ( 2 ) Q = N×D+N× D× H+H × V, (2) Q=N×D+N×D×H+H×V,(2)

- 给定前面的词(previous words)的概率 h ( f o r “ h i s t o r y ” ) h (for “history”) h(for“history”)来预测下一个词的概率 w t ( f o r “ t a r g e t ” ) w_t(for “target”) wt(for“target”),为了最大化预测概率,传统的神经网络概率语言模型都是使用最大似然估计(maximum likelihood ML)来进行训练,以softmax 函数为例:

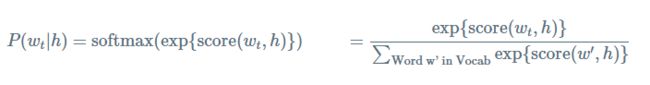
- 其中 s c o r e ( w t , h ) score(w_t,h) score(wt,h) 表示单词 w t w_t wt 与上下文 h h h 的相容性。通过在训练集求解最大log似然来训练该模型。比如,最大化 J M L J_{ML} JML

- 上面等式为正确标准化的语言模型。然而训练它,计算量非常的大。因为每个训练,我对于给定当前的上下文 h h h, 我们需要使用 s c o r e score score 去计算和标准化在语料库 V V V 中所有其他的单词 w ′ w^{'} w′。
2、循环神经网络语言模型(RNNLM)【不使用马尔科夫假设】【Word2vec的对比模型02】


The complexity per training example of the RNN model is
Q = H × H + H × V , ( 3 ) Q = H × H+H × V, (3) Q=H×H+H×V,(3)
where the word representations D have the same dimensionality as the hidden layer H . Again, the term H x V can be efficiently reduced to H x log2(V) by using hierarchical softmax. Most of the complexity then comes from H x H .
3、Word2vec模型(对语言模型的简化)
Word2vec模型输出的词向量:其实是单词同时出现的概率分布(单词共现概率分布)

Word2vec相比较语言模型,大大简化了模型结构,减小了计算量,可以使用更高的维度,更大的数据集;
- Word2vec:使用词预测词;
- 语言模型:使用一系列词来预测词(语言模型:使用一系列词来预测一个词);
- Word2vec模型相当于是对 语言模型 的简化;
- Word2vec模型到底训练了什么:Word2vec训练的是词与词之间 “共现” 的关系;
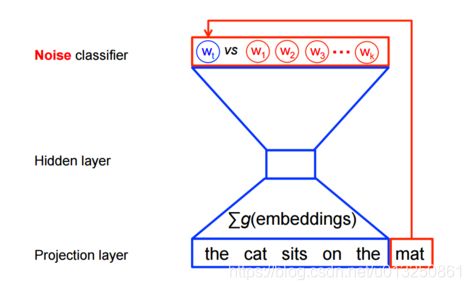
word2vec模型训练时,并不需要一个完全的概率模型。对于相同的上下文,CBOW 和 skip-gram 模型训练使用二分类目标函数(binary classification objective)从 k k k 个假想(imaginary/noise)词 w ^ \hat{w} w^中判别出真实的目标词 w t w_t wt。CBOW模型可以使用下图来描述,对于skip-gram模型只需要简单的把方向反转一下。
数学表示为,对于每个词最大化目标函数为:

- 其中, Q θ ( D = 1 ∣ w , h ) Q_θ(D=1|w,h) Qθ(D=1∣w,h)表示二分类 logistic 回归概率(binary logistic regression probability)在数据集 D D D 上,模型已知单词 w ~ \widetilde{w} w 在上下文 h h h 中,需要学习(或者说计算)的是词向量 θ θ θ。在实践中,我们通过噪音分布(noise distribution)近似抽取k个constrastive words。
- 因此,目标变成了最大化真实词(real words)的概率,最小化噪音词(noise)的概率。从技术的角度,这称之为负采样(Negative Sampling)。.
- 使用这个损失函数有一个很好数学动机:在有限的条件下所提出的更新规则近似的更新了softmax函数。但是计算特别的具有吸引力,因为现在计算这个损失函数我们仅仅需要规格化我们所选择的 k k k 个假想(imaginary/noise)词,而不是整个词汇表 V V V,这使得训练它更快。
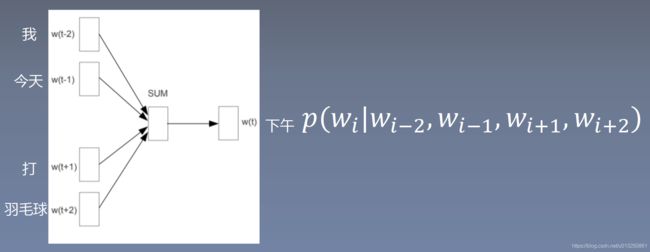
Word2Vec实际是一种浅层的神经网络模型,它有两种网络结构,分别是CBOW(Continues Bag of Words)和Skip-gram。
- CBOW的目标是根据上下文出现的词语的平均来预测当前词的生成概率
- Skip-gram是根据当前词来预测上下文中各词的生成概率。
3.1 CBOW(continuous bags of word)
CBOW模型是给定周围的上下文(surrounding context),再选定某段长度(窗口)作为研究对象,去预测一个中心词(center word)。
如下图,图中窗口大小为9, 使用前后4个词汇对目标词汇进行预测。
- 假设我们给定的训练语料只有一句话: Hope can set you free (愿你自由成长),窗口大小为3;
- 因此模型的第一个训练样本来自Hope can set,
- 因为是CBOW模式,所以将使用Hope和set作为输入,can作为输出,
- 在模型训练时, Hope,can,set等词汇都使用它们的one-hot编码.
- 如图所示: 每个one-hot编码的单词矩阵 A \textbf{A} A(5×1)与 “输入变换矩阵 B \textbf{B} B(3×5)” (即参数矩阵3x5, 这里的3是指最后得到的词向量维度)相乘【 B ⋅ A \textbf{B}·\textbf{A} B⋅A】之后再相加, 得到 上下文表示矩阵 C \textbf{C} C (3x1)。

- 接着, 将 C \textbf{C} C (3x1) 与输出变换矩阵 D \textbf{D} D (5x3)(参数矩阵5x3, 所有的变换矩阵共享参数)相乘【 D ⋅ C \textbf{D}·\textbf{C} D⋅C】, 得到5x1的 结果矩阵 E \textbf{E} E(5×1), 它将与我们真正的目标矩阵即can的one-hot编码矩阵(5x1)进行损失的计算, 然后更新网络参数完成一次模型迭代.

- 最后窗口按序向后移动,重新更新参数,直到所有语料被遍历完成,得到 最终的 “输入变换矩阵 B \textbf{B} B(3×5)” ,这个 最终的 “输入变换矩阵 B \textbf{B} B(3×5)” 与每个词汇的one-hot编码(5x1)相乘,得到的3x1的矩阵就是该词汇的word2vec张量表示.
假设语料库一共有 V V V 个词, 每个词在语料库中取其上下文中共 C C C 个词作为它的上下文。每个词最终使用 N N N 维的embedding来表达。
- NN(神经网络)的输入部分: 那么神经网络的输入就是这C个上下文的词,这些词如何表达呢,最简单的就是用one-hot representation. 每个词的向量大小是 1 × V 1×V 1×V。 所以输入一共是 C C C 个 1 × V 1×V 1×V向量 。
- NN(神经网络)的隐层(Hidden Layer): 这 C C C 个 1 × V 1×V 1×V 向量,都与同一个 V × N V×N V×N 的矩阵相乘,乘完之后把输出的向量做element-wise的average, 作为中间隐层的值,size是 1 × N 1×N 1×N。
- NN的输出层:将隐层乘以一个 N × V N×V N×V 的矩阵产出一个 1 × V 1×V 1×V 的向量,并做softmax, 作为所有词的概率表示。
- 求LOSS:将上面的output与当前的目标词的one-hot representation求loss。
- 模型训练完成后,输入层到隐层的 V × N V×N V×N 的矩阵就是各个词对应的 embedding。
- size是 1 × N 1×N 1×N 的中间隐层的值代表该词的词向量。
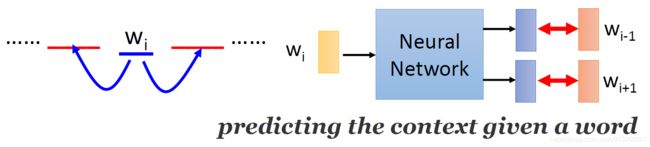
3.2 Skip-Gram
Skip-Gram模型:是给定中心词,再选定某段长度(窗口)作为研究对象, 预测它周围的词。Skip-Gram模型与CBOW模型刚好是相反的。
如下图:窗口大小为9, 使用目标词汇对前后四个词汇进行预测。

3.2.1 Skip-Gram机理解释01
- 假设我们给定的训练语料只有一句话: Hope can set you free (愿你自由成长),窗口大小为3;
- 因此模型的第一个训练样本来自Hope can set,因为是skipgram模式,所以将使用can作为输入 ,Hope和set作为输出,
- 在模型训练时, Hope,can,set等词汇都使用它们的one-hot编码.
- 如图所示: 将can的one-hot编码 A \textbf{A} A(5×1) 与 输入变换矩阵 B \textbf{B} B(3×5) (即参数矩阵3x5, 这里的3是指最后得到的词向量维度)相乘, 得到 目标词汇表示矩阵 C \textbf{C} C (3x1).
- 接着, 将目标词汇表示矩阵 C \textbf{C} C (3x1)与多个 输出变换矩阵 D 1 \textbf{D}_1 D1 (5x3)、 D 2 \textbf{D}_2 D2 (5x3) 相乘, 得到多个5x1的结果矩阵 E 1 \textbf{E}_1 E1(5×1)、 E 2 \textbf{E}_2 E2(5×1), 它将与我们Hope和set对应的one-hot编码矩阵(5x1)进行损失的计算, 然后更新网络参数完成一次模 型迭代.

- 最后窗口按序向后移动,重新更新参数,直到所有语料被遍历完成,得到最终的 输入变换矩阵 B \textbf{B} B(3×5) 即参数矩阵(3x5),这个变换矩阵与每个词汇的one-hot编码(5x1)相乘,得到的3x1的矩阵就是该词汇的word2vec张量表示.
3.2.2 Skip-Gram机理解释02
Skip-Gram输入是中心词,输出是它的上下文词的概率,然后与它的上下文的one-hot representation 求loss.
- 考虑数据集
the quick brown fox jumped over the lazy dog
- 首先,我们形成单词的数据集和上下文,我们可以使用任何有意义的方式定义”上下文”。事实上,我们都知道语法规则(当前目标词的语法依赖关系)。因为,我们可以定义“上下文”(context)为这词左边窗口的单词,而目标词(target word)作为右边的单词。假设窗口(window size)为1。对于上面数据集的(context, target)对为:
[the, brown], quick), ([quick, fox], brown), ([brown, jumped], fox), …
- 其损失函数是定义在整个数据集上,使用梯度递减(SGD)来进行优化, 每一次只使用一个例子。
- 假设上面第一个训练例子(quick, the)在第 t t t 步下进行训练, 及给定单词“input”预测单词“the”。我们选择 num−noise noisy example通过一些noise distribution。为了简单化,假设num−noise=1 和选择单词“sheep”作为noisy example。那么在第 t t t 目标函数为
J N E G ( t ) = l o g Q θ ( D = 1 ∣ t h e , q u i c k ) + l o g Q θ ( D = 0 ∣ s h e e p , q u i c k ) J^{(t)}_{NEG}=logQ_θ(D=1|the,quick)+logQ_θ(D=0|sheep,quick) JNEG(t)=logQθ(D=1∣the,quick)+logQθ(D=0∣sheep,quick) - 目标是就去更新向量参数 θ θ θ 使得目标函数最大化。
- 为了达到这个目的我们可以通过目标函数对向量参数 θ θ θ 进行求导,即 ∂ J N E G ∂ θ \cfrac{∂J_{NEG}}{∂θ} ∂θ∂JNEG,然后沿着梯度的方向更新向量参数 θ θ θ。这个过程一直在训练集上重复计算,这就使得每个单词的向量表示进行了更新,直到但这个模型可以成功的从noise words中判断出real words。

3.2.3 Skip-Gram机理解释03
CBOW和Skip-gram都可以表示成由输入层(Input)、映射层(Projection)和输出层(Output)组成的神经网络。
- 输入层中的每个词由独热编码方式表示,即所有词均表示成一个V维向量,其中V为词汇表中单词的总数。在向量中,每个词都将与之对应的维度置为1,其余维度的值均设为0。
- 在映射层(又称隐含层)中,K个隐含单元的取值可以由V维输入向量以及连接输入和隐含单元之间的V×K维权重矩阵计算得到。
- 输出层向量的值可以通过隐含层向量(K维),以及连接隐含层和输出层之间的K×V维权重矩阵计算得到。
- 输出层也是一个V维向量,每维与词汇表中的一个单词相对应。最后,对输出层向量应用Softmax激活函数,可以计算出每个单词的生成概率。
- 接下来的任务就是训练神经网络的权重,使得语料库中所有单词的整体生成概率最大化。
- 从输入层到隐含层需要一个维度为V×K的权重矩阵,从隐含层到输出层又需要一个维度为K×V的权重矩阵
- 训练得到维度为N×K和K×N的两个权重矩阵之后,可以选择其中一个作为N个词的K维向量表示。
Skip-Gram可以使用下面六步来表示
- 利用One-Hot 编码获取单词 w ( i ) w^{(i)} w(i) 的输入向量 x ⃗ ( 1 × V ) ( i ) = [ 0 1 0 2 ⋯ 1 i ⋯ 0 V ] ( 1 × V ) \vec{x}^{(i)}_{(1×V)}=\begin{bmatrix}0_1&0_2&\cdots&1_i&\cdots&0_V\end{bmatrix}_{(1×V)} x(1×V)(i)=[0102⋯1i⋯0V](1×V),向量大小是 1 × V 1×V 1×V, V V V 表示整体词汇表的大小
- 获取输入向量 ( 其中: θ V × K ( i n ) \textbf{θ}^{(in)}_{V×K} θV×K(in)为输入向量 x ⃗ ( 1 × V ) ( i ) \vec{x}^{(i)}_{(1×V)} x(1×V)(i)的变换矩阵 ) u ⃗ ( 1 × K ) ( i ) = x ⃗ ( 1 × V ) ( i ) ⋅ θ V × K ( i n ) = [ 0 1 0 2 ⋯ 1 i ⋯ 0 V ] ( 1 × V ) ⋅ [ θ 11 ( i n ) θ 12 ( i n ) ⋯ θ 1 n ( i n ) ⋯ θ 1 K ( i n ) θ 21 ( i n ) θ 22 ( i n ) ⋯ θ 2 n ( i n ) ⋯ θ 2 K ( i n ) ⋮ θ i 1 ( i n ) θ i 2 ( i n ) ⋯ θ i n ( i n ) ⋯ θ i K ( i n ) ⋮ θ V 1 ( i n ) θ V 2 ( i n ) ⋯ θ V n ( i n ) ⋯ θ V K ( i n ) ] ( V × K ) = [ θ i 1 ( i n ) θ i 2 ( i n ) ⋯ θ i n ( i n ) ⋯ θ i K ( i n ) ] ( 1 × K ) \begin{aligned}\vec{u}^{(i)}_{(1×K)}&=\vec{x}^{(i)}_{(1×V)}·\textbf{θ}^{(in)}_{V×K}\\&=\begin{bmatrix}0_1&0_2&\cdots&1_i&\cdots&0_V\end{bmatrix}_{(1×V)}·\begin{bmatrix}θ^{(in)}_{11}&θ^{(in)}_{12}&\cdots&θ^{(in)}_{1n}&\cdots&θ^{(in)}_{1K}\\θ^{(in)}_{21}&θ^{(in)}_{22}&\cdots&θ^{(in)}_{2n}&\cdots&θ^{(in)}_{2K}\\\vdots\\θ^{(in)}_{i1}&θ^{(in)}_{i2}&\cdots&θ^{(in)}_{in}&\cdots&θ^{(in)}_{iK}\\\vdots\\θ^{(in)}_{V1}&θ^{(in)}_{V2}&\cdots&θ^{(in)}_{Vn}&\cdots&θ^{(in)}_{VK}\end{bmatrix}_{(V×K)}\\&=\begin{bmatrix}θ^{(in)}_{i1}&θ^{(in)}_{i2}&\cdots&θ^{(in)}_{in}&\cdots&θ^{(in)}_{iK}\end{bmatrix}_{(1×K)}\end{aligned} u(1×K)(i)=x(1×V)(i)⋅θV×K(in)=[0102⋯1i⋯0V](1×V)⋅⎣ ⎡θ11(in)θ21(in)⋮θi1(in)⋮θV1(in)θ12(in)θ22(in)θi2(in)θV2(in)⋯⋯⋯⋯θ1n(in)θ2n(in)θin(in)θVn(in)⋯⋯⋯⋯θ1K(in)θ2K(in)θiK(in)θVK(in)⎦ ⎤(V×K)=[θi1(in)θi2(in)⋯θin(in)⋯θiK(in)](1×K)
- 因为不需要averaging(或者可以理解为,不需要对输入数据规格化),因此 h ⃗ ( 1 × K ) ( i ) = u ⃗ ( 1 × K ) ( i ) \vec{h}^{(i)}_{(1×K)}=\vec{u}^{(i)}_{(1×K)} h(1×K)(i)=u(1×K)(i)
- 单词 w ( i ) w^{(i)} w(i) 的输出向量 v ⃗ ( 1 × V ) ( i ) \vec{v}^{(i)}_{(1×V)} v(1×V)(i) ( 其中: θ K × V ( o u t ) \textbf{θ}^{(out)}_{K×V} θK×V(out)为输出向量 h ⃗ ( 1 × K ) ( i ) \vec{h}^{(i)}_{(1×K)} h(1×K)(i) 的变换矩阵 ) v ⃗ ( 1 × V ) ( i ) = [ v 1 v 2 ⋯ v i ⋯ v V ] ( 1 × V ) = h ⃗ ( 1 × K ) ( i ) ⋅ θ K × V ( o u t ) = [ θ i 1 ( i n ) θ i 2 ( i n ) ⋯ θ i n ( i n ) ⋯ θ i K ( i n ) ] ( 1 × K ) ⋅ [ θ 11 ( o u t ) θ 12 ( o u t ) ⋯ θ 1 v ( o u t ) ⋯ θ 1 V ( o u t ) θ 21 ( o u t ) θ 22 ( o u t ) ⋯ θ 2 v ( o u t ) ⋯ θ 2 V ( o u t ) ⋮ θ i 1 ( o u t ) θ i 2 ( o u t ) ⋯ θ i v ( o u t ) ⋯ θ i V ( o u t ) ⋮ θ K 1 ( o u t ) θ K 2 ( o u t ) ⋯ θ K v ( o u t ) ⋯ θ K V ( o u t ) ] ( K × V ) = x ⃗ ( 1 × V ) ( i ) ⋅ θ V × K ( i n ) ⋅ θ K × V ( o u t ) = [ 0 1 0 2 ⋯ 1 i ⋯ 0 V ] ( 1 × V ) ⋅ [ θ 11 ( i n ) θ 12 ( i n ) ⋯ θ 1 n ( i n ) ⋯ θ 1 K ( i n ) θ 21 ( i n ) θ 22 ( i n ) ⋯ θ 2 n ( i n ) ⋯ θ 2 K ( i n ) ⋮ θ i 1 ( i n ) θ i 2 ( i n ) ⋯ θ i n ( i n ) ⋯ θ i K ( i n ) ⋮ θ V 1 ( i n ) θ V 2 ( i n ) ⋯ θ V n ( i n ) ⋯ θ V K ( i n ) ] ( V × K ) ⋅ [ θ 11 ( o u t ) θ 12 ( o u t ) ⋯ θ 1 v ( o u t ) ⋯ θ 1 V ( o u t ) θ 21 ( o u t ) θ 22 ( o u t ) ⋯ θ 2 v ( o u t ) ⋯ θ 2 V ( o u t ) ⋮ θ i 1 ( o u t ) θ i 2 ( o u t ) ⋯ θ i v ( o u t ) ⋯ θ i V ( o u t ) ⋮ θ K 1 ( o u t ) θ K 2 ( o u t ) ⋯ θ K v ( o u t ) ⋯ θ K V ( o u t ) ] ( K × V ) \begin{aligned}\vec{v}^{(i)}_{(1×V)}&=\begin{bmatrix}v_1&v_2&\cdots&v_i&\cdots&v_V\end{bmatrix}_{(1×V)}=\vec{h}^{(i)}_{(1×K)}·\textbf{θ}^{(out)}_{K×V}\\&=\begin{bmatrix}θ^{(in)}_{i1}&θ^{(in)}_{i2}&\cdots&θ^{(in)}_{in}&\cdots&θ^{(in)}_{iK}\end{bmatrix}_{(1×K)}·\begin{bmatrix}θ^{(out)}_{11}&θ^{(out)}_{12}&\cdots&θ^{(out)}_{1v}&\cdots&θ^{(out)}_{1V}\\θ^{(out)}_{21}&θ^{(out)}_{22}&\cdots&θ^{(out)}_{2v}&\cdots&θ^{(out)}_{2V}\\\vdots\\θ^{(out)}_{i1}&θ^{(out)}_{i2}&\cdots&θ^{(out)}_{iv}&\cdots&θ^{(out)}_{iV}\\\vdots\\θ^{(out)}_{K1}&θ^{(out)}_{K2}&\cdots&θ^{(out)}_{Kv}&\cdots&θ^{(out)}_{KV}\end{bmatrix}_{(K×V)}\\&=\vec{x}^{(i)}_{(1×V)}·\textbf{θ}^{(in)}_{V×K}·\textbf{θ}^{(out)}_{K×V}\\&=\begin{bmatrix}0_1&0_2&\cdots&1_i&\cdots&0_V\end{bmatrix}_{(1×V)}·\begin{bmatrix}θ^{(in)}_{11}&θ^{(in)}_{12}&\cdots&θ^{(in)}_{1n}&\cdots&θ^{(in)}_{1K}\\θ^{(in)}_{21}&θ^{(in)}_{22}&\cdots&θ^{(in)}_{2n}&\cdots&θ^{(in)}_{2K}\\\vdots\\θ^{(in)}_{i1}&θ^{(in)}_{i2}&\cdots&θ^{(in)}_{in}&\cdots&θ^{(in)}_{iK}\\\vdots\\θ^{(in)}_{V1}&θ^{(in)}_{V2}&\cdots&θ^{(in)}_{Vn}&\cdots&θ^{(in)}_{VK}\end{bmatrix}_{(V×K)}\\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad·\begin{bmatrix}θ^{(out)}_{11}&θ^{(out)}_{12}&\cdots&θ^{(out)}_{1v}&\cdots&θ^{(out)}_{1V}\\θ^{(out)}_{21}&θ^{(out)}_{22}&\cdots&θ^{(out)}_{2v}&\cdots&θ^{(out)}_{2V}\\\vdots\\θ^{(out)}_{i1}&θ^{(out)}_{i2}&\cdots&θ^{(out)}_{iv}&\cdots&θ^{(out)}_{iV}\\\vdots\\θ^{(out)}_{K1}&θ^{(out)}_{K2}&\cdots&θ^{(out)}_{Kv}&\cdots&θ^{(out)}_{KV}\end{bmatrix}_{(K×V)}\end{aligned} v(1×V)(i)=[v1v2⋯vi⋯vV](1×V)=h(1×K)(i)⋅θK×V(out)=[θi1(in)θi2(in)⋯θin(in)⋯θiK(in)](1×K)⋅⎣ ⎡θ11(out)θ21(out)⋮θi1(out)⋮θK1(out)θ12(out)θ22(out)θi2(out)θK2(out)⋯⋯⋯⋯θ1v(out)θ2v(out)θiv(out)θKv(out)⋯⋯⋯⋯θ1V(out)θ2V(out)θiV(out)θKV(out)⎦ ⎤(K×V)=x(1×V)(i)⋅θV×K(in)⋅θK×V(out)=[0102⋯1i⋯0V](1×V)⋅⎣ ⎡θ11(in)θ21(in)⋮θi1(in)⋮θV1(in)θ12(in)θ22(in)θi2(in)θV2(in)⋯⋯⋯⋯θ1n(in)θ2n(in)θin(in)θVn(in)⋯⋯⋯⋯θ1K(in)θ2K(in)θiK(in)θVK(in)⎦ ⎤(V×K)⋅⎣ ⎡θ11(out)θ21(out)⋮θi1(out)⋮θK1(out)θ12(out)θ22(out)θi2(out)θK2(out)⋯⋯⋯⋯θ1v(out)θ2v(out)θiv(out)θKv(out)⋯⋯⋯⋯θ1V(out)θ2V(out)θiV(out)θKV(out)⎦ ⎤(K×V)
- 将单词 w ( i ) w^{(i)} w(i) 的输出向量 v ⃗ ( 1 × V ) ( i ) \vec{v}^{(i)}_{(1×V)} v(1×V)(i) 转换成概率, y ⃗ ( 1 × V ) ( i ) = s o f t m a x ( v ⃗ ( 1 × V ) ( i ) ) = [ y 1 y 2 ⋯ y i ⋯ y V ] ( 1 × V ) \vec{y}^{(i)}_{(1×V)}=softmax(\vec{v}^{(i)}_{(1×V)})=\begin{bmatrix}y_1&y_2&\cdots&y_i&\cdots&y_V\end{bmatrix}_{(1×V)} y(1×V)(i)=softmax(v(1×V)(i))=[y1y2⋯yi⋯yV](1×V)
- 使用softmax的word2vec模型,单词 w ( i ) w^{(i)} w(i) 的损失函数为:
p ( w = w ( i ) ∣ v i ; θ ) = = e v i θ i ∑ l = 1 V e v i θ l \begin{aligned} p(w=w^{(i)}|\textbf{v}_i;\textbf{θ})==\cfrac{e^{\textbf{v}_i\textbf{θ}_i}}{\sum^V_{l=1}e^{\textbf{v}_i\textbf{θ}_l}} \end{aligned} p(w=w(i)∣vi;θ)==∑l=1Veviθleviθi
其中:
- K K K:表示训练出来的词向量的维度(可以设定为50/100/200/300)
- v \textbf{v} v:表示所有输出向量 v ⃗ ( 1 ) , v ⃗ ( 2 ) , . . . v ⃗ ( v ) , . . . , v ⃗ ( V ) \vec{v}^{(1)},\vec{v}^{(2)},...\vec{v}^{(v)},...,\vec{v}^{(V)} v(1),v(2),...v(v),...,v(V);
- v i \textbf{v}_i vi:表示输出向量 v ⃗ ( 1 × V ) ( i ) \vec{v}^{(i)}_{(1×V)} v(1×V)(i);
- θ i \textbf{θ}_i θi:表示第 单词 w i w_i wi 的权重向量;
- θ l \textbf{θ}_l θl:表示第 单词 w l w_l wl 的权重向量,其中 l = 1 , 2 , . . . , V l=1,2,...,V l=1,2,...,V;
- w = w ( i ) w=w^{(i)} w=w(i):表示输出向量 v i \textbf{v}_i vi 预测的单词为 w ( i ) w^{(i)} w(i);
- p ( w = w ( i ) ∣ v i ; θ ) p(w=w^{(i)}|\textbf{v}_i;\textbf{θ}) p(w=w(i)∣vi;θ) 输处向量 v ⃗ ( 1 × V ) ( i ) \vec{v}^{(i)}_{(1×V)} v(1×V)(i) 预测的单词为 w ( i ) w^{(i)} w(i) 的预测概率;
- V V V:表示总词汇数量为 V V V;
五、加速训练的技术(层次Softmax、负采样、重采样)
1、Hierarchical Softmax(层次Softmax)【对传统Softmax的优化】
层次化的softmax-对传统softmax的优化方法1
为了提高效率,在fastText中计算分类标签的概率的时候,不再是使用传统的softmax来进行多分类的计算,而是使用的哈夫曼树(Huffman,也成为霍夫曼树),使用层次化的softmax(Hierarchial softmax)来进行概率的计算。
层次Softmax的思想:将Softmax多分类问题转化为多个Sigmoid二分类,且Sigmoid二分类的数量少于 l o g 2 V log_2V log2V,从而大幅度减少计算量;
1.1 哈夫曼树
![]()
1.1.1 哈夫曼树的定义
哈夫曼树概念:给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
1.1.2 哈夫曼树的相关概念
二叉树:每个节点最多有2个子树的有序树,两个子树分别称为左子树、右子树。有序的意思是:树有左右之分,不能颠倒
叶子节点:一棵树当中没有子结点的结点称为叶子结点,简称“叶子”
路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和
树的高度:树中结点的最大层次。包含n个结点的二叉树的高度至少为log2 (n+1)。
1.1.3 哈夫曼树的构造算法
- 把 { W 1 , W 2 , W 3 … W n } \{W_1,W_2,W_3 \dots W_n\} {W1,W2,W3…Wn}看成n棵树的森林
- 在森林中选择两个根节点权值最小的树进行合并,作为一颗新树的左右子树,新树的根节点权值为左右子树的和
- 删除之前选择出的子树,把新树加入森林
- 重复2-3步骤,直到森林只有一棵树为止,概树就是所求的哈夫曼树
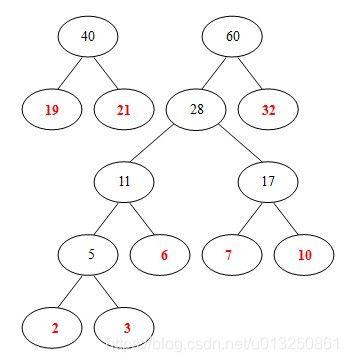
例如:圆圈中的表示每个词语出现的次数,以这些词语为叶子节点构造的哈夫曼树过程如下:
- 从19,21,6,7,10,32,5中选出两个权小结点。选中5,6。同时计算出它们的和11。
-
从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。
【这时选出的两个数字都不是已经构造好的二叉树里面的结点,所以要另外开一棵二叉树;或者说,如果两个数的和正好是下一步的两个最小数的其中的一个,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生长。】

-
从32,28, 40中选出两个权小结点。选中28,32。同时计算出它们的和60。
可见:
- 权重越大,距离根节点越近
- 叶子的个数为n,构造哈夫曼树中新增的节点的个数为n-1
1.2 哈夫曼编码
在数据通信中,需要将传送的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。
例如,需传送的报文为AFTER DATA EAR ARE ART AREA,这里用到的字符集为A,E,R,T,F,D,各字母出现的次数为{8,4,5,3,1,1}。现要求为这些字母设计编码。要区别6个字母,最简单的二进制编码方式是等长编码,固定采用3位二进制,可分别用000、001、010、011、100、101对A,E,R,T,F,D进行编码发送
但是很明显,上述的编码的方式并不是最优的,即整理传送的字节数量并不是最少的。
为了提高数据传送的效率,同时为了保证【前缀编码】,可以使用哈夫曼树生成哈夫曼编码解决问题。【任一字符的编码都不是另一个字符编码的前缀,这种编码称为前缀编码】
可用字符集中的每个字符作为叶子结点生成一棵编码二叉树,为了获得传送报文的最短长度,可将每个字符的出现频率作为字符结点的权值赋予该结点上,显然字使用频率越小权值越小,权值越小叶子就越靠下,于是频率小编码长,频率高编码短,这样就保证了此树的最小带权路径长度效果上就是传送报文的最短长度
因此,求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点,由字符出现频率作为其权值所产生的哈夫曼树的问题。
利用哈夫曼树来设计二进制的前缀编码,
- 既满足【前缀编码】的条件;
- 又保证报文编码总长最短;
下图中label1 .... label6分别表示A,E,R,T,F,D【左节点用1表示,右节点用0表示】
![]()
1.3 梯度计算
![]()
上图中,红色为哈夫曼编码,即label5的哈夫曼编码为1001,那么此时如何定义条件概率 P ( L a b e l 5 ∣ c o n t e x t ) P(Label5|context) P(Label5∣context)呢?
以Label5为例,从根节点到Label5中间经历了4次分支,每次分支都可以认为是进行了一次2分类,根据哈夫曼编码,可以把路径中的每个非叶子节点0认为是负类,1认为是正类(也可以把0认为是正类)
由机器学习课程中逻辑回归使用sigmoid函数进行2分类的过程中,一个节点被分为正类的概率是 σ ( X T θ ) = 1 1 + e − X T θ \sigma(X^{T}\theta) = \frac{1}{1+e^{-X^T\theta}} σ(XTθ)=1+e−XTθ1,被分类负类的概率是: 1 − σ ( X T θ ) 1-\sigma(X^T\theta) 1−σ(XTθ),其中 θ \theta θ就是图中非叶子节点对应的参数 θ \theta θ。
对于从根节点出发,到达Label5一共经历4次2分类,将每次分类结果的概率写出来就是:
- 第一次: P ( 1 ∣ X , θ 1 ) = σ ( X T θ 1 ) P(1|X,\theta_1) = \sigma(X^T\theta_1) P(1∣X,θ1)=σ(XTθ1) ,即从根节点到23节点的概率是在知道X和 θ 1 \theta_1 θ1的情况下取值为1的概率
- 第二次: P ( 0 ∣ X , θ 2 ) = 1 − σ ( X T θ 2 ) P(0|X,\theta_2) =1- \sigma(X^T\theta_2) P(0∣X,θ2)=1−σ(XTθ2)
- 第三次: P ( 0 ∣ X , θ 3 ) = 1 − σ ( X T θ 4 ) P(0 |X,\theta_3) =1- \sigma(X^T\theta_4) P(0∣X,θ3)=1−σ(XTθ4)
- 第四次: P ( 1 ∣ X , θ 4 ) = σ ( X T θ 4 ) P(1|X,\theta_4) = \sigma(X^T\theta_4) P(1∣X,θ4)=σ(XTθ4)
但是我们需要求的是 P ( L a b e l ∣ c o n t e x ) P(Label|contex) P(Label∣contex), 他等于前4词的概率的乘积,公式如下( d j w d_j^w djw是第j个节点的哈夫曼编码)
P ( L a b e l ∣ c o n t e x t ) = ∏ j = 2 5 P ( d j ∣ X , θ j − 1 ) P(Label|context) = \prod_{j=2}^5P(d_j|X,\theta_{j-1}) P(Label∣context)=j=2∏5P(dj∣X,θj−1)
其中:
P ( d j ∣ X , θ j − 1 ) = { σ ( X T θ j − 1 ) , d j = 1 ; 1 − σ ( X T θ j − 1 ) d j = 0 ; P(d_j|X,\theta_{j-1}) = \left\{ \begin{aligned} &\sigma(X^T\theta_{j-1}), & d_j=1;\\ &1-\sigma(X^T\theta_{j-1}) & d_j=0; \end{aligned} \right. P(dj∣X,θj−1)={σ(XTθj−1),1−σ(XTθj−1)dj=1;dj=0;
或者也可以写成一个整体,把目标值作为指数,之后取log之后会前置:
P ( d j ∣ X , θ j − 1 ) = [ σ ( X T θ j − 1 ) ] d j ⋅ [ 1 − σ ( X T θ j − 1 ) ] 1 − d j P(d_j|X,\theta_{j-1}) = [\sigma(X^T\theta_{j-1})]^{d_j} \cdot [1-\sigma(X^T\theta_{j-1})]^{1-d_j} P(dj∣X,θj−1)=[σ(XTθj−1)]dj⋅[1−σ(XTθj−1)]1−dj
在机器学习中的逻辑回归中,我们经常把二分类的损失函数(目标函数)定义为对数似然损失,即
L = − 1 M ∑ l a b e l ∈ l a b e l s l o g P ( l a b e l ∣ c o n t e x t ) L =-\frac{1}{M} \sum_{label\in labels} log\ P(label|context) L=−M1label∈labels∑log P(label∣context)
式子中,求和符号表示的是使用样本的过程中,每一个label对应的概率取对数后的和,之后求取均值。
带入前面对 P ( l a b e l ∣ c o n t e x t ) P(label|context) P(label∣context)的定义得到:
L = − 1 M ∑ l a b e l ∈ l a b e l s l o g ∏ j = 2 { [ σ ( X T θ j − 1 ) ] d j ⋅ [ 1 − σ ( X T θ j − 1 ) ] 1 − d j } = − 1 M ∑ l a b e l ∈ l a b e l s ∑ j = 2 { d j ⋅ l o g [ σ ( X T θ j − 1 ) ] + ( 1 − d j ) ⋅ l o g [ 1 − σ ( X T θ j − 1 ) ] } \begin{aligned} L & = -\frac{1}{M}\sum_{label\in labels}log \prod_{j=2}\{[\sigma(X^T\theta_{j-1})]^{d_j} \cdot [1-\sigma(X^T\theta_{j-1})]^{1-d_j}\} \\ & =-\frac{1}{M} \sum_{label\in labels} \sum_{j=2}\{d_j\cdot log[\sigma(X^T\theta_{j-1})]+ (1-d_j) \cdot log [1-\sigma(X^T\theta_{j-1})]\} \end{aligned} L=−M1label∈labels∑logj=2∏{[σ(XTθj−1)]dj⋅[1−σ(XTθj−1)]1−dj}=−M1label∈labels∑j=2∑{dj⋅log[σ(XTθj−1)]+(1−dj)⋅log[1−σ(XTθj−1)]}
有了损失函数之后,接下来就是对其中的 X , θ X,\theta X,θ进行求导,并更新,最终还需要更新最开始的每个词语词向量
层次化softmax的好处:
- 传统的softmax的时间复杂度为 L(Labels的数量);
- 但是使用层次化softmax之后时间复杂度的log(L) (二叉树高度和宽度的近似);
- 从而在多分类的场景提高了效率。
2、Negative Sampling(负采样)【对传统Softmax的优化】【把多分类问题转为多个二分类问题】

负采样思想:将Softmax多分类问题转化为Sigmoid二分类,且Sigmoid二分类的数量取决于负样本的数量,从而大幅度减少计算量。其中正样本就是原来的中心词+周围词,负样本就是将原来的中心词替换为随机采样的词+周围词;
注意:
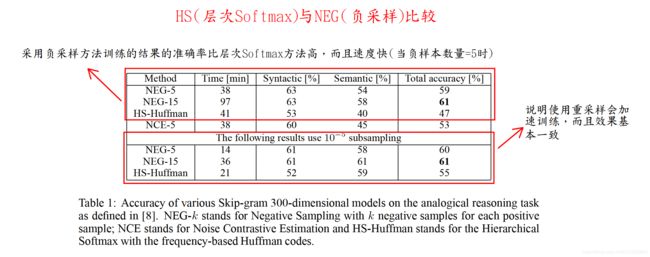
- 负采样优化方式相比较层次Softmax优化方式,效果更好;
- 负采样优化方式相比较层次Softmax优化方式,效率更快;
- 负采样优化方式相比较原始多分类Softmax效果更好。
- 负样本一般取 3~10个;
negative sampling,即每次从除当前label外的其他label中,随机的选择几个作为负样本。具体的采样方法:
如果所有的词(label)的数量为 V V V,那么我们就将一段长度为 1 1 1 的线段分成 V V V份,每份对应所有词(label)中的一个词(label)。
当然每个词(label)对应的线段长度是不一样的:
- 高频label对应的线段长;
- 低频label对应的线段短;
每个词(label)的线段长度由下式决定:
l e n ( l a b e l i ) = c o u n t l a b e l i α ∑ l a b e l k ∈ l a b e l s c o u n t l a b e l k α len(label_i) = \frac{count_{label_i}^{\alpha}}{\sum_{label_k \in labels} count_{label_k}^{\alpha}} len(labeli)=∑labelk∈labelscountlabelkαcountlabeliα
其中:a在fasttext中为0.75,即样本集里负采样被采集到的概率的比值和原来词频比值的 3 4 \cfrac34 43 方根成正比
- 自然语言处理共识:文档或者数据集中出现频率高的词往往携带信息 较少,比如the,is,a,and,而出现频率低的词往往携带信息多。
- 比如:在训练语料中只有3个单词:“apple、eat、drop”,
- 在训练语料中,单词 “apple” 的数量为100,单词 “eat” 的数量为500,单词 “drop” 的数量为500,
- 则这3个单词对应的线段的长度比例不是 1 : 5 : 5 1:5:5 1:5:5,而是 1 3 4 : 5 3 4 : 5 3 4 1^{\frac34}:5^{\frac34}:5^{\frac34} 143:543:543
- 采取负样本的时候这3个单词被采集到的比例分别为 1 3 4 1 3 4 + 5 3 4 + 5 3 4 \cfrac{1^{\frac34}}{1^{\frac34}+5^{\frac34}+5^{\frac34}} 143+543+543143、 5 3 4 1 3 4 + 5 3 4 + 5 3 4 \cfrac{5^{\frac34}}{1^{\frac34}+5^{\frac34}+5^{\frac34}} 143+543+543543、 5 3 4 1 3 4 + 5 3 4 + 5 3 4 \cfrac{5^{\frac34}}{1^{\frac34}+5^{\frac34}+5^{\frac34}} 143+543+543543
- 3 4 \cfrac34 43的目的:减小词频大的词的抽样频率(比如:the/a/an等词频大但是携带的语义信息少的词),增加词频小的词的抽样频率;
在采样前,我们将这段长度为1的线段划分成 M M M等份,这里 M > > V M>>V M>>V,
- 这样可以保证每个label对应的线段都会划分成多个小块;
- 而M份中的每一份都会落在某一个label对应的线段上。
在采样的时候,我们只需要从 M M M个位置中采样出neg个位置就行,此时采样到的每一个位置对应到的线段所属的词就是我们的负样本。
![]()
简单的理解就是,从原来所有的样本中,等比例的选择neg个负样本作(遇到自己则跳过),作为训练样本,添加到训练数据中,和正例样本一起来进行训练。
Negative Sampling也是采用了二元逻辑回归来求解模型参数,通过负采样,我们得到了neg个负例,将正例定义为 l a b e l 0 label_0 label0,负例定义为 l a b e l i , i = 1 , 2 , 3... n e g label_i,i=1,2,3...neg labeli,i=1,2,3...neg,
定义:
- 正例的概率为 P ( l a b e l 0 ∣ context ) = σ ( x k T θ ) , y i = 1 P\left( label_{0}|\text {context}\right)=\sigma\left(x_{\mathrm{k}}^{T} \theta\right), y_{i}=1 P(label0∣context)=σ(xkTθ),yi=1
- 则负例的概率为: P ( l a b e l i ∣ context ) = 1 − σ ( x k T θ ) , y i = 0 , i = 1 , 2 , 3.. n e g P\left( label_{i}|\text {context}\right)=1-\sigma\left(x_{\mathrm{k}}^{T} \theta\right), y_{i}=0,i=1,2,3..neg P(labeli∣context)=1−σ(xkTθ),yi=0,i=1,2,3..neg
- 其中: σ = 1 1 + e − x \sigma=\cfrac{1}{1+e^{-x}} σ=1+e−x1
此时对应的对数似然函数为:
L = y i log ( σ ( x l a b e l 0 T θ ) ) + ∑ i = 1 n e g ( 1 − y i ) log ( 1 − σ ( x l a b e l 0 T θ ) ) L=y_{i} \log \left(\sigma\left(x_{label_0}^{T} \theta\right)\right) + \sum_{i=1}^{n e g} \left(1-y_{i}\right) \log \left(1-\sigma\left(x_{label_0}^{T} \theta\right)\right) L=yilog(σ(xlabel0Tθ))+i=1∑neg(1−yi)log(1−σ(xlabel0Tθ))
对应的损失函数即为:
L = − y i log ( σ ( x l a b e l 0 T θ ) ) − ∑ i = 1 n e g ( 1 − y i ) log ( 1 − σ ( x l a b e l 0 T θ ) ) L=-y_{i} \log \left(\sigma\left(x_{label_0}^{T} \theta\right)\right) - \sum_{i=1}^{n e g} \left(1-y_{i}\right) \log \left(1-\sigma\left(x_{label_0}^{T} \theta\right)\right) L=−yilog(σ(xlabel0Tθ))−i=1∑neg(1−yi)log(1−σ(xlabel0Tθ))
总损失 = 正样本的损失 + k个负样本的损失(k 一般取3~10之间)
具体的训练时候损失的计算过程(源代码已经更新,不再是下图中的代码):
![]()
可以看出:一个neg+1个样本进行了训练,得到了总的损失。
之后会使用梯度上升的方法进行梯度计算和参数更新,仅仅每次只用一波样本(一个正例和neg个反例)更新梯度,来进行迭代更新
具体的更新伪代码如下:
![]()
其中内部大括号部分为w相关参数的梯度计算过程,e为w的梯度和学习率的乘积,具体参考:https://blog.csdn.net/itplus/article/details/37998797
负采样的好处:
- 提高训练速度,选择了部分数据进行计算损失,同时整个对每一个label而言都是一个二分类(把多分类问题转为二分类问题),损失计算更加简单,只需要让当前label的值的概率尽可能大,其他label的都为反例,概率会尽可能小;
- 改进效果,增加部分负样本,能够模拟真实场景下的噪声情况,能够让模型的稳健性更强(提高了模型的稳健性);
在训练神经网络时,每当接受一个训练样本,然后调整所有神经单元权重参数,来使神经网络预测更加准确。换句话说,每个训练样本都将会调整所有神经网络中的参数。
我们词汇表的大小决定了我们skip-gram 神经网络将会有一个非常大的权重参数,并且所有的权重参数会随着数十亿训练样本不断调整。
negative sampling 每次让一个训练样本仅仅更新一小部分的权重参数,从而降低梯度下降过程中的计算量。
如果 vocabulary 大小为1万时, 当输入样本 ( “fox”, “quick”) 到神经网络时, “ fox” 经过 one-hot 编码,在输出层我们期望对应 “quick” 单词的那个神经元结点输出 1,其余 9999 个都应该输出 0。在这里,这9999个我们期望输出为0的神经元结点所对应的单词我们为 negative word. negative sampling 的想法也很直接 ,将随机选择一小部分的 negative words,比如选 10个 negative words 来更新对应的权重参数。
在论文中作者指出指出对于小规模数据集,建议选择 5-20 个 negative words,对于大规模数据集选择 2-5个 negative words.
如果使用了 negative sampling 仅仅去更新positive word- “quick” 和选择的其他 10 个negative words 的结点对应的权重,共计 11 个输出神经元,相当于每次只更新 300 x 11 = 3300 个权重参数。对于 3百万 的权重来说,相当于只计算了千分之一的权重,这样计算效率就大幅度提高。
3、Subsampling of Frequent Words(重采样)
重采样思想:重采样就是将高频词删去一些,将低频词尽量保留,这样就可以训练的更快;
自然语言处理共识:文档或者数据集中出现频率高的词往往携带信息 较少,比如the,is,a,and,而出现频率低的词往往携带信息多。

重采样的原因:
• 想更多地训练重要的词对,比如训练“France”和“Paris”之间的关系比训练“France”和“the”之间的关系要有用。
• 高频词很快就训练好了,而低频次需要更多的轮次。
- 词频越大, f ( w i ) f(w_i) f(wi) 越大, P ( w i ) P(w_i) P(wi) 越大,那么词也就有更大的概率被删除,反之亦然。
- 如果词 w i w_i wi 的词频 f ( w i ) f(w_i) f(wi) 小于等于 t , 那么叫则不会被剔除。
- 优点:加速训练,能够得到更好的词向量。
六、模型复杂度分析
O = E × T × Q O=E×T×Q O=E×T×Q
- O 是训练复杂度 training complexity
- E 是训练迭代次数 number of the training epochs
- T 是数据集大小 number of the words in the training set
- Q 是模型计算复杂度 model computational complexity

模型速度对比:CBOW+NEG > Ship-Gram+NEG > CBOW + HS > Skip-Gram + HS > 前馈神经网络/循环神经网络
1、前馈神经网络语言模型(NNLM)
2、循环神经网络语言模型(RNNLM)
3、Skip-gram模型复杂度
3.1 层次Softmax后的Skip-gram模型复杂度
3.2 负采样后的Skip-gram模型复杂度
4、CBOW复杂度
- N代表周围词的数量
- D代表词向量维度
- V代表词表大小
- K代表负采样数量
七、原论文总结
1、主要创新点
-
提出了一个新的结构:Skip-gram与CBOW。Skip-gram结构是使用中心词预测周围词,CBOW结构是使用周围词预测中心词。Word2vec相比较语言模型,大大简化了模型结构,减小了计算量,可以使用更高的维度,更大的数据集;
- Word2vec:使用词预测词;
- 语言模型:使用一系列词来预测词(语言模型:使用一系列词来预测一个词);
- Word2vec模型相当于是对 语言模型 的简化;
-
提出了层次Softmax、负采样来优化原始的Softmax训练方法,使得训练速度更快;
-
提出了新的词相似度任务(词相似度推理任务),来客观的评价词向量训练的结果;
2、启发点
- 大数据集上的简单模型往往强于小数据集上的复杂模型。
simple models trained on huge amounts of data outperform complex systems trained on less data.(1 Introduction p1) - “King”的词向量减去“Man”的词向量加上“Woman”的词向量和“Queen”的词向量最接近。
vector(”King”) - vector(”Man”) + vector(”Woman”) results in a vector that is closest to the vector representation of the word Queen (1.1 Goals of the Paper p3) - 我们决定设计简单的模型来训练词向量,虽然简单的模型无法像神经网络那么准确地表示数据,但是 可以在更多地数据上更快地训练。
we decided to explore simpler models that might not be able to represent the data as precisely as neural networks, but can possibly be trained on much more data efficiently (3 New Log-linear Models p1) - 我们相信在更大的数据集上使用更大的词向量维度能够训练得到更好的词向量。
We believe that word vectors trained on even larger data sets with larger dimensionality will perform significantly better(5 Examples of the Learned Relationshops p1)
八、Word2vec模型训练
1、数据集下载与抽取
Wikipedia英文语料,包含wikipedia里面的所有文章,可以在https://dumps.wikimedia.org/enwiki/latest/ 上下载。

论文中介绍的词对推理语料,包含五个语义类和九个语法类。其中有8869个语义对样本和10675个语法对样本。可以在http://www.fit.vutbr.cz/~imikolov/rnnlm/word-test.v1.txt 上下载。

抽取文本数据
import logging
import os.path
import sys
from gensim.corpora import WikiCorpus
import time
begin = time.strftime("%Y-%m-%d %H:%M:%S", time.localtime())
if __name__ == '__main__':
program = os.path.basename(sys.argv[0])
logger = logging.getLogger(program)
logging.basicConfig(format='%(asctime)s:%(levelname)s:%(message)s')
logging.root.setLevel(level=logging.INFO)
logger.info("running %s"% ' '.join(sys.argv))
inp,outp = "enwiki-latest-pages-articles14.xml-p7697595p7744800.bz2","wiki_data.txt"
space = ' '
i = 0
output = open(outp,'w',encoding='utf-8')
wiki = WikiCorpus(inp,lemmatize=False,dictionary={ })
for text in wiki.get_texts():
s = space.join(text)+"\n"
output.write(s)
i = i+1
if(i% 10000 == 0):
logger.info("Saved "+str(i) + " articles")
output.close()
logger.info("Finished Saved "+ str(i) +" articles")
end = time.strftime("%Y-%m-%d %H:%M:%S", time.localtime())
print("begin",begin)
print("end ",end)
2、Skip-gram+NGE
2.1 word2id、id2word、正样本、负样本采集
import numpy as np
from collections import deque
class InputData:
def __init__(self, input_file_name, min_count):
self.input_file_name = input_file_name
self.index = 0
self.input_file = open(self.input_file_name, "r", encoding="utf-8")
self.min_count = min_count
self.wordid_frequency_dict = dict()
self.word_count = 0
self.word_count_sum = 0
self.sentence_count = 0
self.id2word_dict = dict()
self.word2id_dict = dict()
self._init_dict() # 初始化字典
self.sample_table = []
self._init_sample_table() # 初始化负采样映射表
self.get_wordId_list()
self.word_pairs_queue = deque()
# 结果展示
print('Word Count is:', self.word_count)
print('Word Count Sum is', self.word_count_sum)
print('Sentence Count is:', self.sentence_count)
def _init_dict(self):
word_freq = dict()
for line in self.input_file:
line = line.strip().split()
self.word_count_sum += len(line) # 统计所有单词数量
self.sentence_count += 1 # 统计所有句子数量
# 统计词频
for i, word in enumerate(line):
if i % 1000000 == 0:
print(i, len(line))
if word_freq.get(word) == None:
word_freq[word] = 1
else:
word_freq[word] += 1
for i, word in enumerate(word_freq):
if i % 100000 == 0:
print(i, len(word_freq))
# 删掉词频小于设定值min_count的词
if word_freq[word] < self.min_count:
self.word_count_sum -= word_freq[word]
continue
# 设置word2id字典
self.word2id_dict[word] = len(self.word2id_dict)
# 设置id2word字典
self.id2word_dict[len(self.id2word_dict)] = word
# 设置word_id2frequency字典
self.wordid_frequency_dict[len(self.word2id_dict) - 1] = word_freq[word]
# 统计词表总大小
self.word_count = len(self.word2id_dict)
# 将文档中所有的单词转为对应的id
def get_wordId_list(self):
self.input_file = open(self.input_file_name, encoding="utf-8")
sentence = self.input_file.readline()
wordId_list = [] # 一句中的所有word 对应的 id
sentence = sentence.strip().split(' ')
for i, word in enumerate(sentence):
if i % 1000000 == 0:
print(i, len(sentence))
try:
word_id = self.word2id_dict[word]
wordId_list.append(word_id)
except:
continue
self.wordId_list = wordId_list
# 获取正样本
def get_batch_pairs(self, batch_size, window_size):
while len(self.word_pairs_queue) < batch_size:
for _ in range(1000):
if self.index == len(self.wordId_list):
self.index = 0
wordId_w = self.wordId_list[self.index] # 中心词
for i in range(max(self.index - window_size, 0), min(self.index + window_size + 1, len(self.wordId_list))):
wordId_v = self.wordId_list[i] # 周围词
if self.index == i: # 上下文=中心词 跳过
continue
self.word_pairs_queue.append((wordId_w, wordId_v))
self.index += 1
result_pairs = [] # 返回mini-batch大小的正采样对
for _ in range(batch_size):
result_pairs.append(self.word_pairs_queue.popleft())
return result_pairs
# 负样本采样
def _init_sample_table(self):
sample_table_size = 1e8
pow_frequency = np.array(list(self.wordid_frequency_dict.values())) ** 0.75
word_pow_sum = sum(pow_frequency)
ratio_array = pow_frequency / word_pow_sum
word_count_list = np.round(ratio_array * sample_table_size)
for word_index, word_freq in enumerate(word_count_list):
self.sample_table += [word_index] * int(word_freq)
self.sample_table = np.array(self.sample_table)
np.random.shuffle(self.sample_table)
# 获取负采样 输入正采样对数组 positive_pairs,以及每个正采样对需要的负采样数 neg_count 从采样表抽取负采样词的id
# (假设数据够大,不考虑负采样=正采样的小概率情况)
def get_negative_sampling(self, positive_pairs, neg_count):
neg_v = np.random.choice(self.sample_table, size=(len(positive_pairs), neg_count)).tolist()
return neg_v
# 估计数据中正采样对数,用于设定batch
def evaluate_pairs_count(self, window_size):
return self.word_count_sum * (2 * window_size) - self.sentence_count * (
1 + window_size) * window_size
# 测试所有方法
if __name__ == "__main__":
test_data = InputData('../data/text8.txt', 1)
test_data.evaluate_pairs_count(2)
pos_pairs = test_data.get_batch_pairs(10, 2)
print('正采样:')
print(pos_pairs)
pos_word_pairs = []
for pair in pos_pairs:
pos_word_pairs.append((test_data.id2word_dict[pair[0]], test_data.id2word_dict[pair[1]]))
print(pos_word_pairs)
neg_pair = test_data.get_negative_sampling(pos_pairs, 3)
print('负采样:')
print(neg_pair)
neg_word_pair = []
for pair in neg_pair:
neg_word_pair.append(
(test_data.id2word_dict[pair[0]], test_data.id2word_dict[pair[1]], test_data.id2word_dict[pair[2]]))
print(neg_word_pair)
2.1 Skip-gram+NGE模型构建
10、超参数选择
2、维基百科语料下载与整理
九、Word2vec预训练词向量下载(用Word2vec模型已经训练好的词向量)
word2vec下载 https://drive.google.com/file/d/0B7XkCwpI5KDYNlNUTTlSS21pQmM/edit
国内地址:https://pan.baidu.com/s/1jJ9eAaE
十、Word Embedding 可视化分析
通过使用tensorboard可视化嵌入的词向量.
# 导入torch和tensorboard的摘要写入方法
import torch
import json
import fileinput
from torch.utils.tensorboard import SummaryWriter
# 实例化一个摘要写入对象
writer = SummaryWriter()
# 随机初始化一个100x50的矩阵, 认为它是我们已经得到的词嵌入矩阵
# 代表100个词汇, 每个词汇被表示成50维的向量
embedded = torch.randn(100, 50)
# 导入事先准备好的100个中文词汇文件, 形成meta列表原始词汇
meta = list(map(lambda x: x.strip(), fileinput.FileInput("./vocab100.csv")))
writer.add_embedding(embedded, metadata=meta)
writer.close()
在终端启动tensorboard服务:
$ tensorboard --logdir runs --host 0.0.0.0
# 通过http://0.0.0.0:6006访问浏览器可视化页面
浏览器展示并可以使用右侧近邻词汇功能检验效果:
![]()
十一、Word Embedding 的应用
- 计算词之间的相似性:直接算词向量之间的距离来表达。
- 看一句话是否通顺:我能想到的思路是把一句用n-gram组成上下文和目标词,然后用NN将上下文作为输出,算跟目标词的loss大小。理论上不通顺的话的loss要比通顺的话的loss明显的大。
- 预测句子下一个词
参考资料:
The Illustrated Word2vec
word2vec 中的数学原理详解
word2vec模型-Skip-Gram 模型数学详解
词表示模型(一)表示学习;syntagmatic与paradigmatic两类模型;基于矩阵的LSA和GloVe
词表示模型(二)基于神经网络的模型:NPLM;word2vec(CBOW/Skip-gram)
词表示模型(三)word2vec(CBOW/Skip-gram)的加速:Hierarchical Softmax与Negative Sampling
nlp中的词向量对比:word2vec/glove/fastText/elmo/GPT/bert
word2vec 中的数学原理详解(五)基于 Negative Sampling 的模型
深度学习语言模型(3)-word2vec负采样(Negative Sampling) 模型(keras版本)
NLP 之 word2vec 以及负采样原理详解
什么是Word2Vec
语言模型 Language Madel 与 word2vec