时空预测模型

STGCN流量预估模型论文解读

《Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting》，Bing Yu, Haoteng Yin, Zhanxing Zhu，Peking University, Beijing, China

背景

流量预估 traffic forecast for short-term (5∼30min), medium and long term (over 30min).
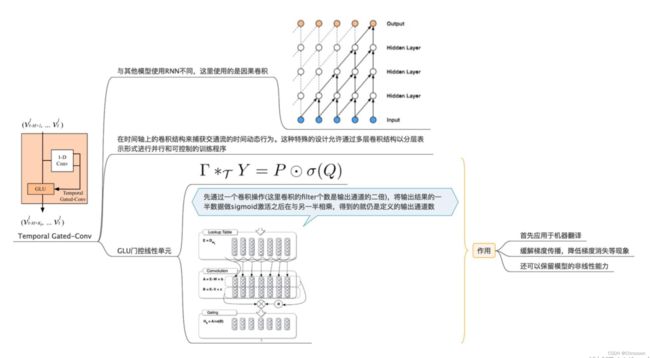
本文提出一个深度学习框架Spatio-Temporal graph convolutional network, 用图网络来建模交通网络，用卷积网络建模time axis. 这是第一次在交通研究中应用纯卷积结构从图结构时间序列中同时提取时空特征。

交通预测数据

这是经典的时间序列预测问题，用vt及其前M个时间点，预测v_t+1及其后H个时间点：

在这里，我们用graph来表示每一个v_t, 如下图

每一个v_t（即每一张图）表示一个时刻，包含n个顶点，模拟的是n个传感器的结果。每M张图构成一条数据

模型结构

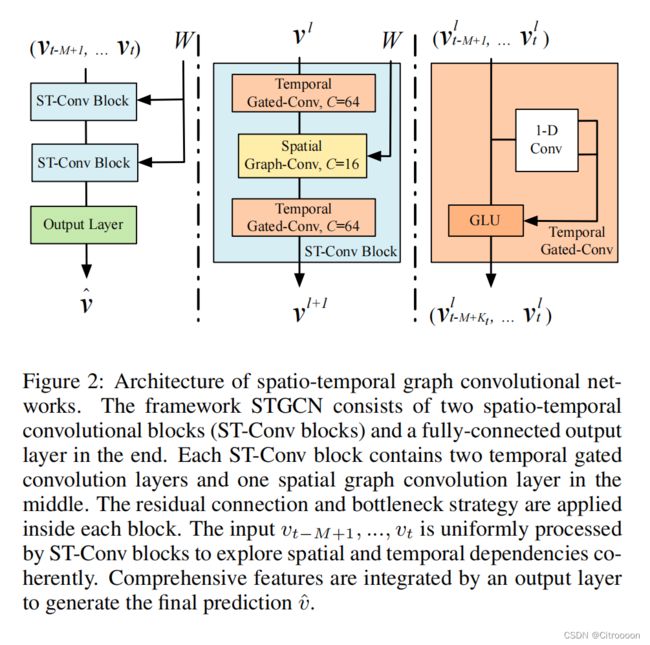
模型结构：两层时空卷积块+输出层，其中，时空卷积块由 时域卷积块1 + 空域卷积块 + 时域卷积块2 组成

时域卷积块在每个时间步之间进行；空域卷积块在每个时间步内进行

时域卷积块

输入：$X\in R^{M\ast n\ast C_i}$, 文中$C_i$设为了1
对于每一个节点来说，维度是$R^{M\ast C_i}$，
卷积的kernel维度是$K\in R^{K\ast 2C_o}$,
所以，一维卷积的输出维度是$R^{(M-K+1)\ast 2C_o}$

P、Q is split in half with the same size of channels， 维度分别是$R^{(M-K+1)\ast C_o}$, 再通过一个GLU激活层

对于一张完整的时空卷积图，输入是$X\in R^{M\ast n\ast C_i}$， 输出是$Y\in R^{(M-K+1)\ast C_0}$

空域卷积块

切比雪夫图卷积公式：

解释：
$\tilde{L}=\frac{2L}{{\lambda }_{max}}-I_n$,
$L=I_n-D^{-1/2}A{D}^{-1/2}$, 是图的对称归一化laplacian矩阵
$D$为图的度矩阵，$A$为图的邻接矩阵, we can further assume that ${\lambda }_{max}\approx 2$

$T_k(\tilde{L})$是$k$阶在scaled拉普拉斯量处求值的切比雪夫多项式, 即它取决于中心节点的最近的$k^{th}$order 的邻居节点（邻居节点和中心节点的距离最大为K）
$T_i(x)=2x{T}_{i-1}(x)-T_{i-2}(x)$, 其中$T_0=1,T_1=x$

$\theta$是多项式系数

假设，传播邻居层数$k=1，{\lambda }_{max}=2$， 可得

最终，带有C_i个channels的图卷积可以表示为：

输出$X\in R^{M\ast n\ast C_i}$, 输出$Y\in R^{M\ast n\ast C_o}$

输出层

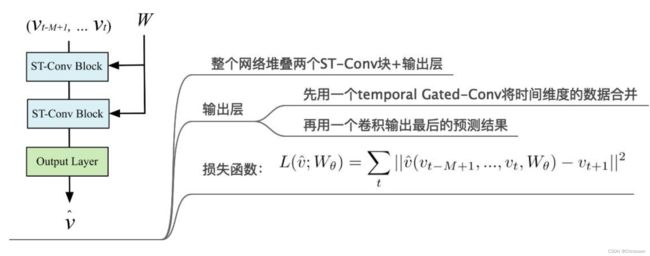
输出层 = 时域卷积层 + 全连接层
每经过一个时域卷积块，维度减少$K-1$, 一共会经过四个，所以，输入输出层的维度是$R^{M-4(K-1)\ast n\ast C_o}$
我们将时域卷积层的kernel维度和input一样，这样可以将其映射到n*C_o上，就是最终的输出
全连接层$wx+b$，$w\in R^{C_o}$, 最终$v_t\in R^n$

Ref

STGCN 是处理结构化时间序列的通用框架。它不仅能够解决交通网络建模和 预测问题，而且可以应用于更一般的时空序列学习任务。
时空卷积块结合了图卷积和门控时间卷积，能够提取出最有用的空间特征，并 连贯地捕捉到最基本的时间特征。
该模型完全由卷积结构组成，在输入端实现并行化，参数更少，训练速度更 快。更重要的是，这种经济架构允许模型以更高的效率处理大规模网络。