指纹和掌纹识别中的霍夫变换

霍夫（Hough）变换最早是由美国原子能委员会的Hough在一项专利中提出的，用于检测高能核物理中粒子的直线运动轨迹。Rosenfeld（1969）将霍夫变换引入了图像处理领域。Duda和Hart（1972）提出采用法线式的直线表示方法进行霍夫变换。之后经过众多研究者的发展和推广（Illingworth and Kitler，1988），霍夫变换能检测各种可参数化的形状（如圆、椭圆）、任意形状、一般物体（如人体、汽车）等，成为图像处理和计算机视觉领域最为实用的方法之一。这些霍夫变换的推广被统称为广义霍夫变换，其中涉及概率投票的方法也被称为概率霍夫变换。

基于霍夫变换的直线检测方法（Hart，2009）

霍夫变换在指纹和掌纹识别领域也有许多应用。下面举几个例子。

指纹姿态估计

指纹的姿态指其中心和角度。指纹姿态估计是指从指纹图像估计其中心和角度。可能有人会问，为什么要做手指的姿态估计呢？在人脸识别/虹膜识别中，姿态估计和归一化是显然需要的，研究者已经发表了大量的论文解决这个问题。但是在指纹识别领域，姿态估计是一个长期被忽视或者回避的问题。为什么被忽视？一方面的原因是，即使指纹鉴定专家也不容易给出指纹姿态的精确定义；另一方面的原因是，难以设计鲁棒的算法从各种类型的指纹图像估计姿态。因此过去的指纹比对算法都没有做姿态的约束，而是设计容忍各种旋转、偏移的比对算法。

指纹姿态。左：非接触指纹照片，右：接触式指纹图像

但是如果能够估计出准确可靠的姿态，那就会对指纹比对技术的设计方案产生重大的影响。当做两个指纹的细节点匹配时，如果是在完全不知道两个指纹姿态的情况下，只看局部的描述子的相似度来找对应点，那么就会有许多候选点需要考虑；但如果已知两个指纹的姿态了，就可以把候选点减少很多，这对于后面匹配速度和精度都有极大的帮助。

Yang等人（2014）提出了一种基于霍夫变换的指纹姿态估计算法。该算法需要在离线阶段学习局部方向块的空间分布概率，以便在线阶段进行概率霍夫变换（即概率投票）。首先从训练指纹图像的方向场中找出大量方向块，将它们聚类为若干原型块；然后对于各个原型块，估计其在指纹图像中的分布概率。

在线阶段对于给定的一幅指纹图像，根据各个局部指纹块对指纹中心进行概率投票，并叠加起来。最后检测霍夫空间中最亮的点，就得到了指纹中心。通过对该指纹的方向场做各种旋转，对各个角度的指纹做中心预测，最后选择响应最强的角度作为指纹的方向。

估计指纹中心的流程图（Yang等人，2014）

掌纹姿态估计

掌纹识别在识别犯罪嫌疑人方面非常有价值，是公安部门不可缺少的办案工具。实际中由于缺乏严格的数据质量控制手段，在利用活体掌纹采集、掌纹卡片扫描等方法得到的掌纹图像中，掌纹的姿态并不总是一致的。设计对于旋转和平移不变的掌纹匹配算法并不困难，但这种算法的计算量非常高。

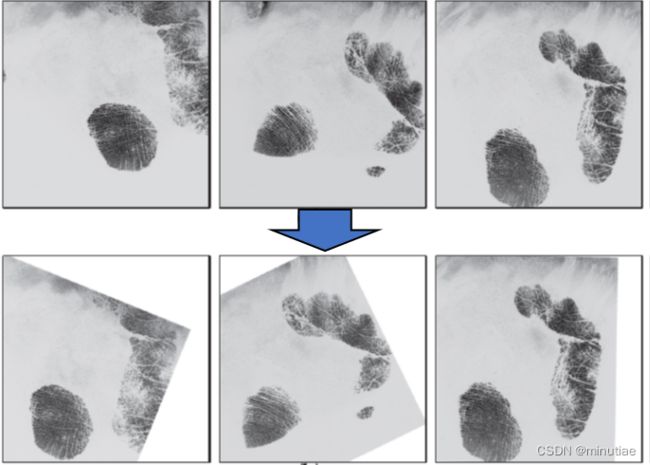
Dai等人（2012）提出了将任意掌纹与掌纹平均方向场进行配准的方法，实现了掌纹图像的姿态统一，并在此基础上实现了高速而准确的掌纹比对。该配准方法就是一种广义霍夫变换方法。作者在离线阶段将一组掌纹手工对齐，然后计算它们的平均方向场，作为姿态归一化的参照物。在在线阶段，对于待配准的掌纹，首先计算其方向场，然后利用霍夫变换将该方向场与平均方向场进行配准。霍夫变换的投票是由任意一对方向元素投出的，而且使用了与局部方向方差相关的权重，以提高某些方向稳定位置的相对重要性。下图为同一个掌纹的三幅图像，其原本图像的姿态差异很大，经过该算法的校正后，统一为一致的姿态。

不同姿态的三个掌纹被校正到统一的姿态（Dai等人，2012）

 

指纹配准

指纹比对是要确定两幅指纹图像是否来自同一手指。指纹比对分为两步：指纹配准和指纹匹配（计算匹配分数，简称打分）。主流的指纹配准技术是将指纹视为细节点集合，将指纹配准转化为点集匹配问题。一个细节点的基本属性有位置和角度。假设两幅指纹图像之间的空间变换近似为刚体变换，只需要一对细节点就可以估算出刚体变换的旋转和平移参数。Hough变换空间包括三个维度：x平移，y平移，旋转。对于所有可能匹配的细节点对，分别估计变换参数，对变换空间中对应的参数进行投票。最后检测变换空间的峰值，即可得到两幅指纹之间的空间变换。这个基本的方法见Ratha等人（1996）。

当两幅指纹图像之间的重叠区域特别小、共同细节点数量很少时，上述方法可能检测不到正确的空间变换参数。Paulino等人（2012）的做法是，在对一对细节点的空间变换进行投票时，利用局部区域描述子（即细节点描述子），计算出二者的相似度，做加权投票。这可以提高变换空间中正确变换参数的相对大小，提高算法的正确率。下图的例子为现场指纹与滚动指纹的配准。该现场指纹面积很小，仅有6个细节点。基本的霍夫变换方法失败了，而基于描述子的霍夫变换方法可以得到正确的空间变换。

当两个指纹的共同细节点数目很少时，基于细节点描述子的霍夫变换方法（Paulino等人，2012）表现优于基本的霍夫变换方法。从左到右：现场指纹及细节点，滚动指纹及细节点，基本霍夫变换的配准结果，基于细节点描述子的霍夫变换的配准结果。

参考文献

P. V. C. Hough, “Method and means for recognizing complex patterns”, U.S. Patent 3 069 654, Dec. 18, 1962.

A. Rosenfeld, Picture Processing by Computer. New York: Academic, 1969, pp. 335–336.

R. O. Duda and P. E. Hart, “Use of the Hough transformation to detect lines and curves in pictures”, Commun. ACM, vol. 15, no. 1, pp. 11–15,1972.

J. Illingworth and J. Kitler, “A survey of the Hough transform”, Comput. Vis., Graph., Image Process. Arch., vol. 44, no. 1, pp. 87–116, 1988.

P. E. Hart, "How the Hough transform was invented [DSP History]". IEEE Signal Processing Magazine, 26(6), 18-22, 2009.

X. Yang, J. Feng, J. Zhou, "Localized dictionaries based orientation field estimation for latent fingerprints", IEEE Transactions on Pattern Analysis and Machine Intelligence, 36 (5), 955-969, 2014.

J. Dai, J. Feng, J. Zhou, "Robust and efficient ridge-based palmprint matching", IEEE Transactions on Pattern Analysis and Machine Intelligence, 34(8), 1618-1632, 2012.

N. K. Ratha, K. Karu, S. Chen, A. K. Jain, "A Real-Time Matching System for Large Fingerprint Databases", IEEE Transactions on Pattern Analysis and Machine Intelligence, 18(8), 799-813, 1996.

A. A. Paulino, J. Feng, A. K. Jain, "Latent fingerprint matching using descriptor-based hough transform", IEEE Transactions on Information Forensics and Security, 8 (1), 31-45, 2012.