吃瓜教程task04 第5章 神经网络
第5章 神经网络
2022/5/28 雾切凉宫 至5.3节/视频P7
文章目录
- 第5章 神经网络
-
- 5.1 神经元模型
-
- p7 神经网络
-
- p7.1 M-P神经元
- 5.2 感知机与多层网络
-
-
- p7.2 感知机
-
- 感知机模型
- 感知机学习策略
- 感知机学习算法
- p7.3 神经网络
-
- 多层前馈网络
- 误差逆传播算法(BP)
-
- 误差逆传播算法(BP)
-
5.1 神经元模型
p7 神经网络
p7.1 M-P神经元
M-P神经元:接收n个输入(通常是来自其他神经元),并给各个输入赋予权重计算加权和,然后和自身特有的阈值θ进行比较(作减法),最后经过激活函数f(模拟“抑制"和“激活”)处理得到输出(通常是给下一个神经元)
y = f ( ∑ i = 1 n w i x i − θ ) = f ( w T x + b ) y=f(\sum_{i=1}^nw_ix_i-θ)=f(w^Tx+b) y=f(i=1∑nwixi−θ)=f(wTx+b)
常见激活函数f:
- sgn函数
- sigmoid函数
5.2 感知机与多层网络
p7.2 感知机
感知机模型
激活函数为sgn (阶跃函数)的神经元
y = s g n ( w T x − θ ) y=sgn(w^Tx-θ) y=sgn(wTx−θ)
x为特征向量,(w,θ)为神经元参数(权重,阈值)
感知机学习策略
随机初始化w, b,将全体训练样本代入模型找出误分类样本,假设此时误分类样本集合为M∈T,对任意一个误分类样本来说,以下公式恒成立:
( y ^ − y ) ( w T x − θ ) > = 0 (\hat{y}-y)(w^Tx-θ)>=0 (y^−y)(wTx−θ)>=0
所以,给定数据集T,其损失函数可以定义为:
L ( w , θ ) = ∑ x ∈ M ( y ^ − y ) ( w T x − θ ) L(w,θ)=\sum_{x∈M}(\hat{y}-y)(w^Tx-θ) L(w,θ)=x∈M∑(y^−y)(wTx−θ)
显然,,此损失函数是非负的。如果没有误分类点,损失函数值是0。而且,误分类点越少,误分类点离超平面越近,损失函数值就越小。
具体地,给定数据集
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } T = \{(x_1, y_1), (x_2,y_2),...,(x_n,y_n)\} T={(x1,y1),(x2,y2),...,(xn,yn)}
其 中 x i ∈ R , y i ∈ { 0 , 1 } , 求 参 数 w , θ , 使 其 为 极 小 化 损 失 函 数 的 解 : 其中x_i∈R,y_i∈\{0,1\},求参数w,θ,使其为极小化损失函数的解: 其中xi∈R,yi∈{0,1},求参数w,θ,使其为极小化损失函数的解:
m i n L ( w , θ ) = m i n w , θ ∑ x i ∈ M ( y i ^ − y i ) ( w T x i − θ ) min L(w,θ)= {min}_{w,θ}\sum_{x_i∈M}(\hat{y_i}- y_i)(w^Tx_i-θ) minL(w,θ)=minw,θxi∈M∑(yi^−yi)(wTxi−θ)
其中M为误分类样本集合。若将阈值θ看作一个固定输入为-1的“哑节点”,即:
− θ = − 1 ∗ W n + 1 = x n + 1 ∗ w n + 1 -θ=-1*W_{n+1}=x_{n+1}*w_{n+1} −θ=−1∗Wn+1=xn+1∗wn+1
根据该式,可将要求解的极小化问题进一步简化为:
m i n w L ( w ) = m i n w ∑ x i ∈ M ( y i ^ − y i ) w T x i min_{w}L(w)=min_w\sum_{x_i∈M}(\hat{y_i}-y_i)w^Tx_i minwL(w)=minwxi∈M∑(yi^−yi)wTxi
感知机学习算法
当误分类样本集合M固定时、那么可以求得损失函数L(w)的梯度为:
▽ w L ( w ) = ∑ ( x i ∈ M ) ( y i ^ − y i ) x i ▽_wL(w)=\sum_{(x_i∈M)}(\hat{y_i}-y_i)x_i ▽wL(w)=(xi∈M)∑(yi^−yi)xi
感知机的学习算法具体采用的是随机梯度下降法,也就是极小化过程中不是一次使M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。所以权重w的更新公式为:(η为学习率)
w = w + △ w w=w+△w w=w+△w
△ w = − η ( y i ^ − y i ) x i = η ( y i − y i ^ ) x i △w=-η(\hat{y_i}-y_i)x_i=η(y_i-\hat{y_i})x_i △w=−η(yi^−yi)xi=η(yi−yi^)xi
p7.3 神经网络
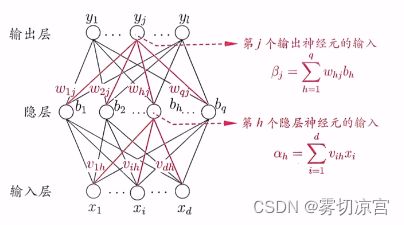
多层前馈网络
多层前馈网络:每层神经元与下一层神经完全互连,神经元之间不存在同层连接,也不存在跨层连接。 (隐层阈值γn, 输出层阈值θj)
一般地,按照需要完成的任务来选择损失函数,比如
-
一个多输出回归任务:损失函数一般采用均方误差。
-
一个分类任务:损失函数使用交叉熵。
误差逆传播算法(BP)
基于随机梯度(损失函数的梯度)下降的参数更新算法:
w = w + △ w w=w+△w w=w+△w
△ w = − η ▽ w E △w=-η▽_wE △w=−η▽wE
使用交叉熵。
误差逆传播算法(BP)
基于随机梯度(损失函数的梯度)下降的参数更新算法:
w = w + △ w w=w+△w w=w+△w
△ w = − η ▽ w E △w=-η▽_wE △w=−η▽wE
其中只需推导出▽wE这个损失函数E关于参数w的一阶偏导数(梯度)即可(链式求导)。值得一提的是,由于NN(x )通常是极其复杂的非凸函数,不具备像凸函数这种良好的数学性质,因此随机梯度下降不能保证一定能走到全局最小值点,更多情况下走的都是局部极小值点。