【电机控制理论】三相BLDC/PMSM电机的基本数学变换及其电流环控制

1.为什么要做坐标变换？

电机除了转，就只能转了，但它简单的现象背后却是一个典型的非线性、强耦合、多变量、周期性的机电能量转换的复杂系统。

1.1 电机控制的目的

电机控制无非就是达到三个控制目的：
①转矩控制
②速度控制
③位置控制
其中转矩控制是核心，因为矢量控制的核心目标就是为了让电机以稳定的转矩旋转，在这个基础上再实现速度环、位置环。举例子他们三环内外放置时的关系：在电流-速度环中，不同的电流电机内部就产生不同情况的磁场，面对不同负载，电流大，磁场强，转速快。在电流-速度-位置环中，位置是速度在时间上的积分，我们希望以稳定的速度走一段位置，那么对应速度，也对应着某一种电流情况。显然，电流环是最内环(重要)的
以三相无刷电机举例，它的三相对称正弦电流可以这样表示：
Ia=Im * cos(wt+φ)
Ib=Im * cos(wt+φ-120°)
Ic=Im * cos(wt+φ+120°)

1.2 电机控制系统的复杂性

电机控制终究是力矩的控制，速度控制与位置控制都是基于力矩控制的，而力矩与电流息息相关。所以在设计电机驱动的硬件时，运算放大器对电流的采样，转换上无论是速度还是精度，都有较高要求。
如果我们原搬不动地使用上述的Ia,Ib和Ic，会怎么样呢？
我们需要从其中求解iA,iB,iC（定子电流瞬时值）,ia,ib,ic（转子电流瞬时值）,并作如下处理（还只是冰山一角）：

我们在求解三相电机转矩与励磁之间的关系时，会用到一系列微分方程，直接求解非常困难，而进行坐标变换，目的就是为了绕过含微积分的数学关系式，解耦三相电机转矩与励磁之间的关系，简化问题。

1.3 旨在简化问题

上述建立的电机转矩动态数学模型，是一组含有时变系数的非线性微分方程，难以直接分析和求解。需要简化，简化的基本方法是坐标变换。
所谓坐标变换就是将方程中的一组变量用一组新的变量来代替，或者说用新的坐标系去替换原来的坐标系，以便使分析、计算得以简化。若新、旧变量之间为线性关系，则变换为线性变换，电机分析中常用到的坐标变换都是线性变换。
目的很明确，强耦合系统解耦，非线性系统线性化处理。
我们希望三相电机像直流电机那样简单易控。
克拉克Clark变换帮我们将三相电机等效成两相电机；
帕克Park变换帮我们将电流解耦，使我们控制交流电流像控制直流那样简便。

2.克拉克Clark变换(3s/2s)

2.1 变换思想

克拉克变换将三相系统（在 abc 坐标系中）的时域分量转换为正交静止坐标系 (αβ) 中的两个分量。我们要把三相电机等效成两相电机，方便后续分析。

设Is为三相对称正弦电流的合成矢量。
Is=Ia+Ib+Ic

Clark变换旨在利用向量分解，将三相坐标合成为两相坐标
根据投影，我们得到：
i_alpha=Ia-Ib * cos(π/3)-Ic * cos(π/3)
i_beta=Ib * cos(π/6)-Ic * cos(π/6)
用矩阵可以表示:

2.1 原始变换(k=1)

根据三相电机简化模型，由电路基尔霍夫定律：
Ia+Ib+Ic=0
展开后易得：
i_alpha=3/2 * Ia
i_beta=√3/2 * Ia + √3Ib

由动态图我们可以看到，通过克拉克变换，我们成功地将三相电机等效为了两相电机，这就是克拉克变换的意义。
通过类比，试想：部分步进电机就是两相电机，无需克拉克变换，直接使用两相的数据代入帕克变换中直接解耦，是否也能做FOC控制？

2.2 幅值不变原则的变换(k=2/3)

由Is易知：
Is=Ia+Ib+Ic=i_alpha+i_beta
故i_alpha+i_beta的模值依然是3/2 * Im
若我们希望合成前后的模值不变，即依然是Im,那我们就在前面乘以一个系数k，对其缩减，显而易见按，3/2k=1
那么k1=2/3
代入易得：
i_alpha= Ia
i_beta=1/√3 * Ia + 2/√3Ib

为什么要幅值不变？
是为了后续SVPWM调制时，确保输出电压在正六边形内，使输出波形最大不失真。

2.3 功率不变原则的变换(k=√(2/3))

<1>变换前
P0=Um * Im * 3（三相）
<2>变换后：
U=3/2 * k * Um
I=3/2 * k * Im
P=UI * 2（两相）
令P0=P:
解有等功率变换系数 k2=√(2/3)
代入易得：
i_alpha= √6/2 * Ia
i_beta=√2/2 * Ia + √2Ib

2.4 它的反变换

通过2.2或2.3的结论可逆推得到。

3.帕克Park变换（2s/2r）

3.1 变换思想

即使我们已经通过克拉克变化将三相变成了两相，但是从i_alpha和i_beta的展开式中，依旧含有时间t，电流依旧由时间决定，分析起来还是很复杂。
帕克变换中，在克拉克变换的基础上，试图将表达式中的时间t消去，就是帕克变换的核心思想和目的。

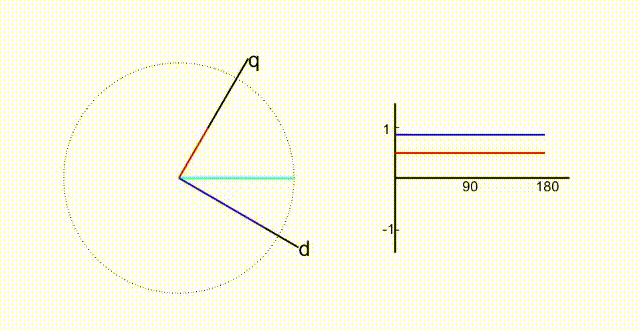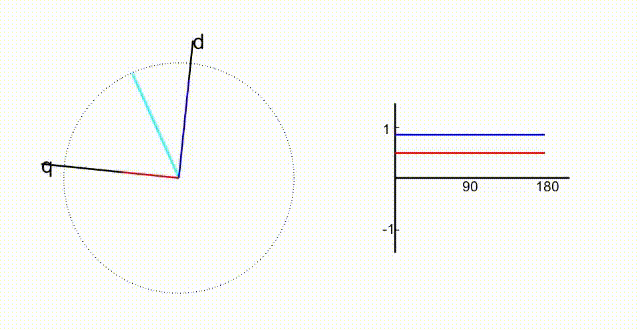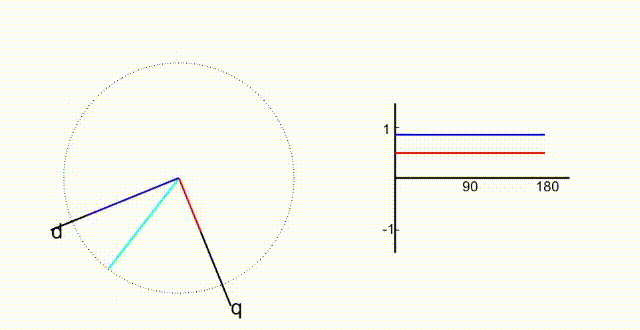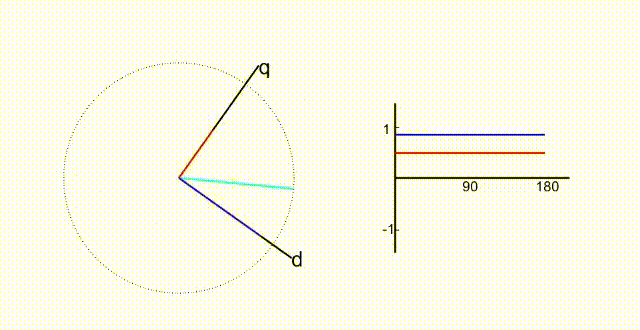
如图，旋转坐标轴以w的角速度旋转。

3.2.变换公式

根据投影分析，我们得到：
i_d=i_alpha * cosθ+ i_beta * sinθ
i_q=-i_alpha * sinθ+i_beta * cosθ

3.3 变换推导

这里使用等幅值原则的结论进行推导。
我们尝试进一步简化：

从结论知，只要φ不变，id与iq在时域上，必是直线。
因为iq垂直与定子磁场，所以力矩只由iq决定；
而id与定子磁场平行，不作用于力矩控制。

3.4 它的反变换

v_alpha =v_d * cosθ-v_q * sinθ
v_beta=v_d * sinθ+v_q * cosθ

4.坐标变换结论

4.1 两种变换的总结

4.2 机械角度与电角度

p是电机的极对数
电角度=p * 机械角度
我们代入公式中计算的，用的都是电角度
我们Ia，Ib与Ic中的wt+φ，wt+φ-120°，wt+φ+120°指的都是电角度。

4.3 wt，θ，φ，和p的关系

p：电机的极对数，可以帮我们求电角度
wt，θ，φ三者都是电角度
wt=θ，是两相旋转坐标轴与两相静止坐标轴的夹角。
φ就有意思了，它是定子磁场和转子磁场的角度。

当定子磁场和转子磁场的角度为90°，即φ=90°时，转矩最大

5.坐标变换的变种

对于三相静止坐标系(3s)

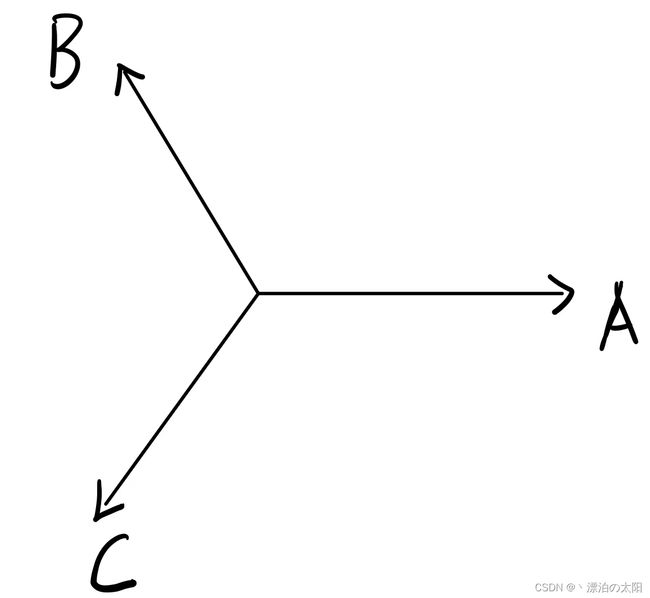
我们分析时，要转换成两相静止坐标系(2s),也就是Clarke变换，但是Clarke变换对于不同开发厂商，它所使用的变换形式不一样。

5.1 Clarke变换

<1>α水平向左为正方向，β垂直向上为正方向(我们所用的)：

<2>α水平向右为正方向，β垂直向下为正方向(ST所用的)：

可以看出，和我们数学上的推理相符，Iβ‘在<1>的Iβ基础上取反了。
<3>总结
我们习惯于使用的是以下形式：

有一些开发厂商使用的是以下形式，比如ST电机库:

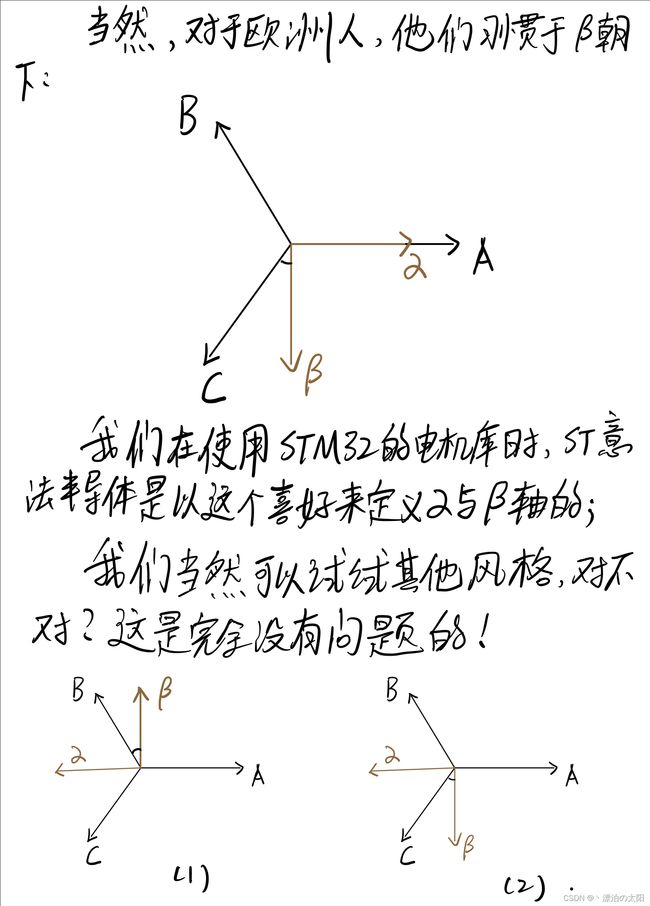
我们当然可以选取其他的方向作为正方向进行变换，这个交给读者自行去尝试了！

5.2 相应的Park变换

无论我们在Clarke变换中怎么样选取两个轴的正方向，我们的Park变换都要与之对应。


<1>θe=0时，选取为d轴与A轴对齐的时候：


<2>θe=0时，选取为q轴与A轴对齐的时候：

5.3 Summary

我们可以由ST的资料对比分析以下：

对于坐标变换的理解，可以参考文章：
FOC中对坐标变换的理解及电角度校准

6.电流控制

6.1 恒转矩角δ=90°控制(id=0法)

(此法仅适用于表贴式PMSM电机)
(无刷直流电机BLDC一般是表贴式)
当id为0时，电流全部用于iq来进行力矩控制，发挥其最大转矩。
也就是说，定子磁场与转子磁场相差90°的时候，转子以最大力矩旋转！
为什么力矩控制时，大多数时id=0矢量控制法来做转矩控制？
因为id=0时，表贴式PMSM电机转矩：
Tem=3/2 * p*φ_f * iq
这时候转矩方程是比较简单的，所以我们使id控制为0；
其中φ_f是磁链，式子中可以看到，在id=0情况下，转矩是和iq直接相关的，转矩控制的本质就是电流控制。
注意：在硬件设计时，电流追踪检测的部分，一定不能设计出错。

6.2 表贴式PMSM电机的D/Q轴数学模型

后续…【核心内容，毕业后公布】

6.3 电流环的参数整定(精准理论法)

…【核心内容，毕业后公布】

6.4 Id与Iq的简单前馈解耦器

虽然我们通过帕克变换成功把励磁电流和转矩电流电流分离出来，但Iq会影响Id,Id也会影响Iq，他们还是有耦合的现象，并不像我们理想中那样他们只要单独控制就可以简单完事的。
所以在进行PI控制时，我们要根据它们的耦合关系做修改，当然，这种耦合是比较简单的，没有微积分运算：
具体的耦合关系：

R：定子电阻,单位为Ω
Ls：定子电感，单位为H
D:微分算子
w：电气频率，也就是你的电角速度，单位为rad/s
Ke：反电动势常数，单位为V·s/rad

所以在我们输出Vd或者Vq时，我们要在单片机加入这种耦合关系：
简单的前馈解耦器：
Vd=Vd_pid_output-w * Ls * iq_real
Vq=Vq_pid_output+w(Ls * id_real+Ke)