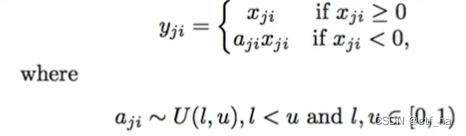1、常用激活函数:Sigmoid、Tanh、ReLU、LReLU、RReLU、ELU
目录
- 常用激活函数介绍
-
- 1、 Sigmoid函数
- 2、Tanh / 双曲正切激活函数
- 3、ReLU(rectified linear unit)修正线性单元函数
- 4、LReLU(Leaky ReLU)带泄露线性整流函数
- 5、RReLU(Randomized Leaky ReLU)随机修正线性单元
- 6、PReLU (parametric ReLU)参数化线性整流函数
- 6、ELU (Exponential Linear Units) 指数线性修正
常用激活函数介绍
1、 Sigmoid函数
Sigmoid 是常用的非线性的激活函数,能够把连续值压缩到0-1区间上。
其函数表达式为:
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
其对应导函数为:
f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f^{'}(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x))
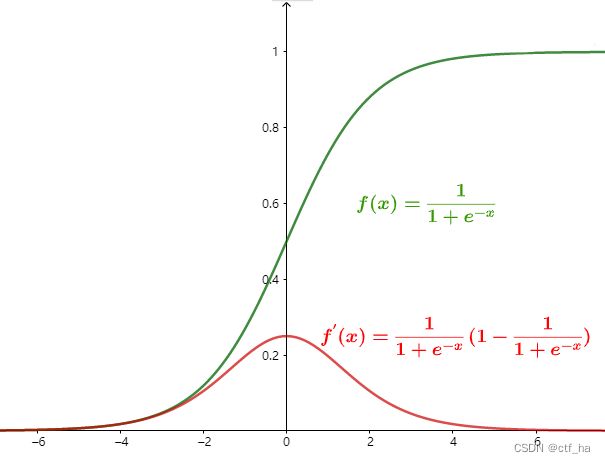
由图发现, lim x → ∞ \lim_{x \to \infty} limx→∞时, f ′ ( x ) = 0 f^{'}(x)=0 f′(x)=0,将具有这种性质的激活函数叫作软饱和激活函数。Sigmoid导数的取值范围在0~0.25之间。
sigmoid函数求导过程:
f ′ ( x ) = ( 1 1 + e − x ) ′ = ( ( 1 + e − x ) − 1 ) ′ = ( − 1 ) ( 1 + e − x ) − 2 ⋅ ( e − x ) ′ = ( 1 + e − x ) − 2 ( e − x ) = e − x ( 1 + e − x ) 2 = e − x + 1 − 1 ( 1 + e − x ) 2 = 1 1 + e − x − 1 ( 1 + e − x ) 2 = 1 1 + e − x ( 1 − 1 1 + e − x ) = f ( x ) ( 1 − f ( x ) ) \begin{aligned} f'(x) &= (\frac{1}{1+e^{-x}})' \\ &=((1+e^{-x})^{-1})' \\ &=(-1)(1+e^{-x})^{-2} \cdot (e^{-x})' \\ &=(1+e^{-x})^{-2}(e^{-x}) \\ &=\frac{e^{-x}}{(1+e^{-x})^{2}} \\ &=\frac{e^{-x}+1-1}{(1+e^{-x})^{2}} \\ &=\frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x})^2} \\ &=\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}}) \\ &=f(x)(1-f(x)) \end{aligned} f′(x)=(1+e−x1)′=((1+e−x)−1)′=(−1)(1+e−x)−2⋅(e−x)′=(1+e−x)−2(e−x)=(1+e−x)2e−x=(1+e−x)2e−x+1−1=1+e−x1−(1+e−x)21=1+e−x1(1−1+e−x1)=f(x)(1−f(x))
优点
- Sigmoid函数连续,光滑,严格单调,以(0,0.5)中心对称,良好的阈值函数。
- Sigmoid是便于求导的平滑函数,即f′(x)=f(x)(1−f(x)),计算方便,节省计算时间。
- Sigmoid的值域是在(0,1)区间,具有很好的性质,可以被表示为预测概率(逻辑回归处理二分类问题)或者用于对每个神经元的输出进行了归一化。
- 梯度平滑,避免输出值跳跃。
缺点
- 容易出现梯度消失(gradient vanishing),即 lim x → ∞ \lim_{x \to \infty} limx→∞时, f ′ ( x ) = 0 f^{'}(x)=0 f′(x)=0。
- Sigmoid 的输出不是 0 均值(zero-centered),降低权重更新的效率。
- 函数的敏感区间较短,(-2,2)之间较为敏感,超过区间,则处于饱和状态。
- Sigmoid 函数执行指数运算,计算机运行得较慢。
输出不是zero-centered,为什么会降低权值更新的效率?
https://zhuanlan.zhihu.com/p/70821070
【梯度消失】:梯度趋近于零,网络权重无法更新或更新的很微小,网络训练再久也不会有效果;
【梯度爆炸】:梯度呈指数级增长,变的非常大,然后导致网络权重的大幅更新,使网络变得不稳定。
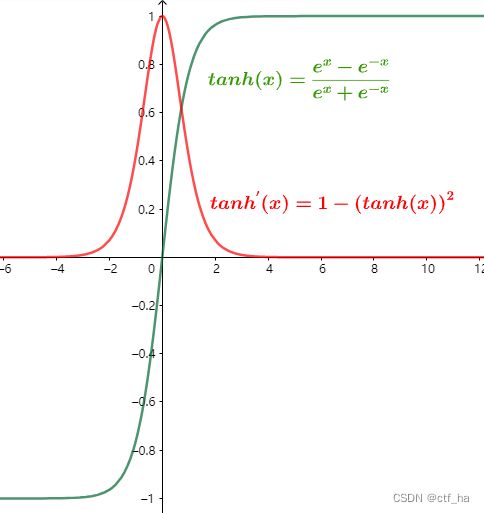
2、Tanh / 双曲正切激活函数
tanh也是一种非常常见的激活函数,与sigmoid相比,它的输出均值为0,这使得它的收敛速度要比sigmoid快,减少了迭代更新的次数。
其函数表达式为:
t a n h ( x ) = e x − e − x e x + e − x tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} tanh(x)=ex+e−xex−e−x
其对应导函数为:
t a n h ′ ( x ) = 1 − ( t a n h ( x ) ) 2 tanh^{'}(x)=1-(tanh(x))^2 tanh′(x)=1−(tanh(x))2
tanh(x)函数求导过程:
已知: e − x 导 数 为 − e − x e^{-x}导数为-e^{-x} e−x导数为−e−x, e x 导 数 为 e x e^{x}导数为e^{x} ex导数为ex
t a n h ′ ( x ) = ( e x − e − x e x + e − x ) ′ = ( ( e x − e − x ) ( e x + e − x ) − 1 ) ′ = ( e x + e − x ) ( e x + e − x ) − 1 + ( e x − e − x ) ( e x + e − x ) − 2 ( e x − e − x ) = 1 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − ( t a n h ( x ) ) 2 \begin{aligned} tanh^{'}(x) &= (\frac{e^x-e^{-x}}{e^x+e^{-x}})' \\ &=((e^x-e^{-x})(e^x+e^{-x})^{-1})' \\ &=(e^x+e^{-x})(e^x+e^{-x})^{-1}+(e^x-e^{-x})(e^x+e^{-x})^{-2}(e^x-e^{-x})\\ &= 1- \frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2}\\ &=1-(tanh(x))^2 \\ \end{aligned} tanh′(x)=(ex+e−xex−e−x)′=((ex−e−x)(ex+e−x)−1)′=(ex+e−x)(ex+e−x)−1+(ex−e−x)(ex+e−x)−2(ex−e−x)=1−(ex+e−x)2(ex−e−x)2=1−(tanh(x))2
优点
- 输出均值是0(zero-centered),使得其收敛速度要比Sigmoid快,减少迭代次数。
- 部分解决了sigmoid关于zero-centered的输出问题。导数范围变大在(0,1)之间,而sigmoid在 (0,0.25)之间,梯度消失问题有所缓解。
缺点
- 梯度消失现象依然存在。
- 比sigmod更复杂的幂运算。
实际上,Tanh激活函数相当于sigmoid函数的平移:
t a n h ( x ) = 2 s i g m o i d ( 2 x ) − 2 tanh(x)=2sigmoid(2x)-2 tanh(x)=2sigmoid(2x)−2
3、ReLU(rectified linear unit)修正线性单元函数
ReLU是针对sigmoid和tanh的饱和性而提出的新的激活函数。,当 x>0 的时候,不存在饱和问题,所以ReLU能够在 x>0 的时候保持梯度不衰减,从而缓解梯度消失的问题。这让我们可以以有监督的方式训练深度神经网络,而无需依赖无监督的逐层训练。
其函数表达式为:
f ( x ) = { m a x ( 0 , x ) , x ≥ 0 0 , x < 0 f(x)= \left\{ \begin{aligned} &max(0,x) ,x≥0\\ &0,x<0 \end{aligned} \right. f(x)={max(0,x),x≥00,x<0
- 从计算角度上,sigmoid和Tanh激活函数均需要计算指数,复杂度高,而ReLU只需要一个阈值即可得到激活值。
- ReLU的非饱和性可以有效地解决梯度消失的问题,提供相对宽的激活边界。
- ReLU的单侧抑制提供了网络的稀疏激活性。
【稀疏激活性】:从信号方面来看,即神经元同时只对输入信号的少部分选择性响应,大量信号被刻意的屏蔽了,这样可以提高学习的精度,更好更快地提取稀疏特征。当 x<0 时,ReLU 硬饱和,而当 x>0 时,则不存在饱和问题。ReLU 能够在x>0 时保持梯度不衰减,从而缓解梯度消失问题。
缺点
-
ReLU的输出不是zero-centered。
-
训练过程中会导致神经元死亡。这是由于函数f(x)=max(,x)导致负梯度在经过该ReLU单元时被置为0,且在之后不被任何数据激活,即流经该神经元的梯度永远为0,不对任何数据产生响应。在实际训练中,如果学习率(Learning Rate)设置较大,会导致超过一定比例的神经元不可逆死亡,进而导致参数梯度无法更新,整个训练过程失败。
-
对参数初始化和学习率非常敏感;
-
要防范ReLU的梯度爆炸;
【神经元死亡】:随着训练的推进,部分输入会落入硬饱和区,导致对应权重无法更新。
4、LReLU(Leaky ReLU)带泄露线性整流函数
为了解决了Relu会杀死一部分神经元的情况,人们设计了ReLU的变种Leaky ReLU。
其函数表达式为:
f ( x ) = { x , x ≥ 0 a x , x < 0 f(x)= \left\{ \begin{aligned} &x ,x≥0\\ &ax,x<0 \end{aligned} \right. f(x)={x,x≥0ax,x<0
其中a一般为很小的正常数(如0.01),是个固定值,即实现了单侧抑制,又保留了部分负梯度信息以至不完全丢失。但另一方面,a值的选择增加了问题难度,需要较强的人工先验或者重复训练以确定合适的参数值。
-
部分神经元不会出现死亡的情况。
-
Leaky ReLU线性、非饱和的形式,在SGD中能够快速收敛。
-
计算速度都比sigmoid和tanh快,Leaky ReLU函数只有线性关系,不需要指数计算。
缺点
- Leaky ReLU函数中的α,需要较强的人工先验或者重复训练以确定合适的参数值。
- 尽管该函数在所有点处都是连续的,但在 x=0 处不可微,即在 x=0 处,图形的斜率突然变化,。因此,在梯度下降期间,它的值会“反弹”。尽管如此,Leaky ReLU 在实践中表现得非常好
5、RReLU(Randomized Leaky ReLU)随机修正线性单元
根据α的选择策略不同,演变出RReLU和PReLU 。
RReLU训练时给定范围内随机选择α,α是从一个高斯分布U(l,u)中随机出来的,然后再测试过程中进行修正,一般预估时固定为平均值。
优点
- RReLU引入了随机因素,可以减少过拟合的风险;
缺点
6、PReLU (parametric ReLU)参数化线性整流函数
PReLU是LReLU的改进,可以自适应地从数据中学习参数。
PReLU 函数表达式为:
f ( x ) = { x , x ≥ 0 a x , x < 0 f(x)= \left\{ \begin{aligned} &x ,x≥0\\ &ax,x<0 \end{aligned} \right. f(x)={x,x≥0ax,x<0
其中α是一个可调整的参数,范围0-1,它控制着负值部分在何时饱和,避免ReLU死掉问题。
优点
- 负值域,PReLU 的斜率较小,可以避免 Dead ReLU 问题;
- PReLU 在负值域是线性运算;
缺点
- 在小数据有过拟合风险
6、ELU (Exponential Linear Units) 指数线性修正
ELU 是在2015年出现的一种激活函数,是为解决ReLU存在的问题而提出。
与其他非饱和激活函数类似,ELU 没有梯度消失和梯度爆炸的问题。和Leaky-ReLU和 PReLU 类似,与 ReLU 不同的是,ELU 没有神经元死亡的问题。它已被证明优于 ReLU 及其变体,如 Leaky-ReLU(LReLU) 和 Parameterized-ReLU(PReLU)。与 ReLU 及其变体相比,使用 ELU 可以减少神经网络的训练时间和更高的准确度。
其函数表达式为:
f ( x ) = { x , x ≥ 0 α ( e x − 1 ) , x < 0 f(x)= \left\{ \begin{aligned} &x ,x≥0\\ &\alpha(e^x-1),x<0 \end{aligned} \right. f(x)={x,x≥0α(ex−1),x<0
优点
- 它在所有点上都是连续且可微的。
- 与其他线性非饱和激活函数(如 ReLU 及其变体)相比,它可以缩短训练时间。
- 与 ReLU 不同,它没有神经元死亡的问题。这是因为 ELU 的梯度对于所有负值都是非零的。
- 作为非饱和激活函数,它不会遭受梯度爆炸或消失的问题。
- 与其他激活函数(如 ReLU 和变体、Sigmoid 和双曲正切)相比,它实现了更高的准确度。
缺点
- 与 ReLU 及其变体相比,它的计算速度较慢,因为负输入涉及非线性。然而,在训练期间,这被 ELU 更快的收敛所补偿。但在测试期间,ELU 的执行速度会比 ReLU 及其变体慢。
理论上虽然好于ReLU,但在实际使用中目前并没有好的证据ELU总是优于ReLU。
https://deeplearninguniversity.com/elu-as-an-activation-function-in-neural-networks/
研究论文https://arxiv.org/pdf/1511.07289