常用的激活函数总结
| 激活函数名 | 表达式 | 导数表达式 |
|---|---|---|
| sigmoid | f(x)= 1 1 + e − x \frac{1}{1+e^-x} 1+e−x1 | f’(x)=f(x)(1-f(x)) |
| Tanh | f(x) = tanh(x) = e x − e − x e x + e − x \frac{e^x-e^-x}{e^x+e^-x} ex+e−xex−e−x | f’(x)=1- ( ( f x ) ) 2 ((fx))^2 ((fx))2 |
| Relu | f ( x ) = m a x ( 0 , x ) = { 0 x ≤ 0 x x > 0 f(x)=max(0,x) = \begin{cases}0&\text{$x\leq0 $ }\\x&\text{$x>0$} \end{cases} f(x)=max(0,x)={0xx≤0 x>0 | f ′ ( x ) = { 0 x ≤ 0 1 x > 0 f'(x)= \begin{cases}0&\text{$x\leq0 $ }\\1&\text{$x>0$} \end{cases} f′(x)={01x≤0 x>0 |
| LeakyReLU | f ( x ) = m a x ( 0.001 x , x ) = { 0.001 x x ≤ 0 x x > 0 f(x)=max(0.001x,x)=\begin{cases}0.001x&\text{$x\leq0 $ }\\x&\text{$x>0$} \end{cases} f(x)=max(0.001x,x)={0.001xxx≤0 x>0 | f ′ ( x ) = { 0.001 x ≤ 0 1 x > 0 f'(x)= \begin{cases}0.001&\text{$x\leq0 $ }\\1&\text{$x>0$} \end{cases} f′(x)={0.0011x≤0 x>0 |
| PReLU | f ( x ) = m a x ( 0.001 x , x ) = { α x x ≤ 0 x x > 0 f(x)=max(0.001x,x)=\begin{cases}\alpha x&\text{$x\leq0 $ }\\x&\text{$x>0$} \end{cases} f(x)=max(0.001x,x)={αxxx≤0 x>0 | f ′ ( x ) = { α x ≤ 0 1 x > 0 f'(x)= \begin{cases}\alpha &\text{$x\leq0 $ }\\1&\text{$x>0$} \end{cases} f′(x)={α1x≤0 x>0 |
| ELU | f ( x ) = { x x ≥ 0 α ( e x − 1 ) x<0 f(x)=\begin{cases}x&\text {$x \geq 0$}\\ \alpha (e^x -1) &\text{x<0}\end{cases} f(x)={xα(ex−1)x≥0x<0 | f ′ ( x ) = { 1 x ≥ 0 α e x x < 0 f'(x)=\begin{cases}1& \text{$x \geq 0$}\\\alpha e^x &\text{$x<0$} \end{cases} f′(x)={1αexx≥0x<0 |
| Maxout | f ( x ) = m a x ( w 1 T x + b 1 , w 2 T x + b 2 ) f(x)=max(w_1^T x + b_1,w_2^T x + b_2) f(x)=max(w1Tx+b1,w2Tx+b2) | ¥ f ( x ) = m a x ( w 1 , w 2 ) f(x)=max(w_1,w_2) f(x)=max(w1,w2) |
各种激活函数图像
sigmoid

Tanh

RELU

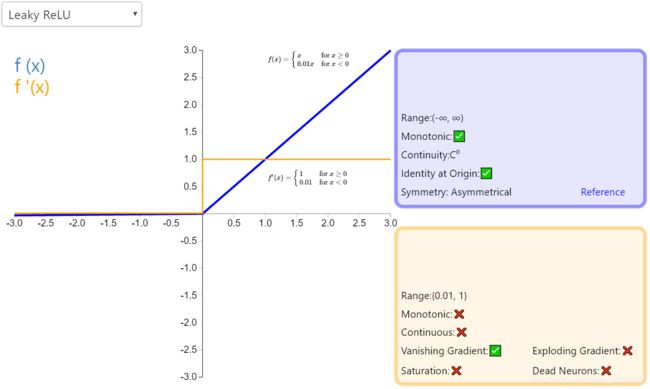
Leaky ReLU
这是由激活函数的性质所决定来, 一般来说, 激活函数都具有以下性质:
非线性: 首先,线性函数可以高效可靠对数据进行拟合, 但是现实生活中往往存在一些非线性的问题(如XOR), 这个时候, 我们就需要借助激活函数的非线性来对数据的分布进行重新映射, 从而获得更强大的拟合能力. (这个是最主要的原因, 其他还有下面这些性质也使得我们选择激活函数作为网络常用层)
可微性: 这一点有助于我们使用梯度下降发来对网络进行优化
单调性: 激活函数的单调性在可以使单层网络保证网络是凸优化的
f(x)≈x:
当激活满足这个性质的时候, 如果参数初值是很小的值, 那么神经网络的训练将会很高效(参考ResNet训练残差模块的恒等映射); 如果不满足这个性质, 那么就需要用心的设值初始值( 这一条有待商榷 )
如果不使用激活函数, 多层线性网络的叠加就会退化成单层网络,因为经过多层神经网络的加权计算,都可以展开成一次的加权计算
更形象的解释
对于一些线性不可分的情况, 比如XOR, 没有办法直接画出一条直线来将数据区分开, 这个时候, 一般有两个选择.
如果已知数据分布规律, 那么可以对数据做线性变换, 将其投影到合适的坐标轴上, 然后在新的坐标轴上进行线性分类
而另一种更常用的办法, 就是使用激活函数, 以XOR问题为例, XOR问题本身不是线性可分的,
关于各个激活函数的比较和适用场景
神经元饱和问题: 当输入值很大或者很小时, 其梯度值接近于0, 此时, 不管从深层网络中传来何种梯度值, 它向浅层网络中传过去的, 都是趋近于0的数, 进而引发梯度消失问题
zero-centered: 如果数据分布不是zero-centered的话就会导致后一层的神经元接受的输入永远为正或者永远为负, 因为 ∂f∂w=x
, 所以如果x的符号固定,那么 ∂f∂w 的符号也就固定了, 这样在训练时, weight的更新只会沿着一个方向更新, 但是我们希望的是类似于zig-zag形式的更新路径 (关于非0均值问题, 由于通常训练时是按batch训练的, 所以每个batch会得到不同的信号, 这在一定程度上可以缓解非0均值问题带来的影响, 这也是ReLU虽然不是非0 均值, 但是却称为主流激活函数的原因之一)
各种激活函数优缺点分析
| 激活函数名 | 优势 | 劣势 | 适用场景 |
|---|---|---|---|
| Sigmoid | 可以将数据值压缩到[0,1]区间内 | 1. 神经元饱和问题 2.sigmoid的输出值域不是zero-centered的 3. 指数计算在计算机中相对来说比较复杂 |
在logistic回归中有重要地位 |
| Tanh | 1. zero-centered: 可以将 (−∞,+∞) 的数据压缩到 [−1,1] 区间内 2.完全可微分的,反对称,对称中心在原点 |
1. 神经元饱和问题 2. 计算复杂 |
在分类任务中,双曲正切函数(Tanh)逐渐取代 Sigmoid 函数作为标准的激活函数 |
| ReLU | 1. 在 (0,+∞) ,梯度始终为1, 没有神经元饱和问题 2. 不论是函数形式本身,还是其导数, 计算起来都十分高效 3. 可以让训练过程更快收敛(实验结果表明比sigmoid收敛速度快6倍) 4. 从生物神经理论角度来看, 比sigmoid更加合理 |
1. 非zero-centered 2. 如果输入值为负值, ReLU由于导数为0, 权重无法更新, 其学习速度可能会变的很慢,很容易就会”死”掉(为了克服这个问题, 在实际中, 人们常常在初始化ReLU神经元时, 会倾向于给它附加一个正数偏好,如0.01) |
在卷积神经网络中比较主流 |
| LeakyReLU | 1. 没有神经元饱和问题 2. 计算高效 3. 收敛迅速(继承了ReLU的优点) 4. 神经元不会”死”掉(因为在负值时, 输出不为0, 而是x的系数0.001) |
||
| PReLU | 1. 没有神经元饱和问题 2. 计算高效 3. 收敛迅速(继承了ReLU的优点) 4. 神经元不会”死”掉(因为在负值时, 输出不为0, 而是x的系数 α ) 5. 相对于Leaky ReLU需要通过先验知识人工赋值, PReLU通过迭代优化来自动找到一个较好的值, 更加科学合理, 同时省去人工调参的麻烦 |
||
| ELU | 1. 拥有ReLU所有的优点 2. 形式上更接近于zero-centered 3. 在面对负值输入时,更加健壮 |
1. 引入了指数计算, 使计算变的复杂 | |
| Maxout | Maxout 1. 跳出了点乘的基本形式 2. 可以看作是ReLU和Leaky ReLU 的一般化形式 3. linear Regime(啥意思?)! 4. 在所有输入范围上都没有神经元饱和问题 5. 神经元永远不会”死”掉 6. 拟合能力非常强,它可以拟合任意的的凸函数。作者从数学的角度上也证明了这个结论,即只需2个maxout节点就可以拟合任意的凸函数了(相减),前提是”隐含层”节点的个数可以任意多 |
1. 使得神经元个数和参数个数加倍, 导致优化困难 |
激活函数的使用原则
1. 优先使用ReLU, 同时要谨慎设置初值和学习率 ( 实际操作中,如果你的learning rate 很大,那么很有可能你网络中的40%的神经元都 “dead” 了。 当然,如果你设置了一个合适的较小的learning rate,这个问题发生的情况其实也不会太频繁 )
2. 尝试使用LeakyReLU/PReLU/Maxout/ELU等激活函数
3. 可以试下tanh, 但是一般不会有太好的结果
4. 不要使用sigmoid
其他激活函数
https://www.jiqizhixin.com/articles/2017-10-10-3
参考
激活函数总结