经典神经网络学习笔记之LeNet（附带代码）

       本文是对经典论文“Gradient-Based Learning Applied to Document Recognition”的阅读笔记之一，主要介绍LeNet的结构以及参数个数的计算，结合“DeepLearning for Computer Vision with Python starter bundle”所介绍的原理和实验所写。笔者才疏学浅，还望指教。

一、理论部分

        LeNet首次出现是在1998年的论文中，基于梯度的学习应用于文档识别[19]。 正如论文的名称所暗示的那样，作者实施LeNet背后的动机主要是光学字符识别（OCR）。LeNet架构简单明了（在内存占用方面很小），非常适合学习CNN的基础知识。在本章中，我们将寻求在1998年的论文中复制类似于LeCun的实验。 我们首先回顾一下LeNet架构，然后使用Keras实现网络。 最后，我们将在MNIST数据集上评估LeNet的手写数字识别。  

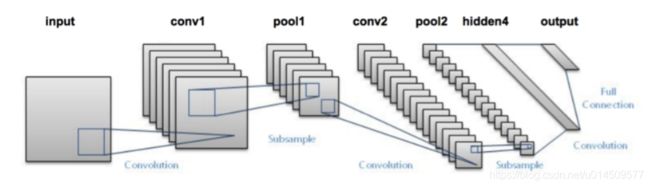
        先上两张结构图：

                      LeNet架构由两个系列的CONV => TANH => POOL层集组成，后跟一个完全连接的层和softmax输出。

                      图片来源：http：//pyimg.co/ihjsx

• input: 在原始的架构中，神经网络的输入是一张  的灰度图像，不过这里我们选用的dataset是cifar10，是RGB图像，也就是  噢
• conv1: 第一层是一个卷积层啦，卷积核(kernel size)大小  ,步长(stride)为  ，不进行padding哦，所以刚才的输入图像，经过这层后会输出6张  的特征图(feature map)
• maxpooling2: 接下来是一个降采样层，用的是maxpooling哦，stride为  , kernel size为  ，恩，所以很明显subsampling之后，输出6张 的feature map哦
• conv3: 第三层又是一个卷积层，kernel size和stride均与第一层相同噢，不过最后要输出16张feature map哦
• maxpooling4:第四层，恩，又是一个maxpooling
• fc5：对，第五层开始就是全连接(fully connected layer)层了哦，把第四层的feature map摊平，然后做最直白的举证运算哦，输入是120个结点
• fc6：输出是84个结点哦
• output：我们的dataset是cifar10,刚好也是10类哦，所以就是接一个softmax分成10类哦

                                                                                 LeNet架构中每一层的size
         LeNet + MNIST的组合能够在CPU上轻松运行，使初学者可以轻松地在深度学习和CNN中迈出第一步。 在许多方面，LeNet + MNIST是应用于图像分类的“Hello，World”等效的深度学习。 LeNet体系结构由以下层组成，使用以下的CONV => ACT => POOL模式：

       在这里，LeNet架选择使用tanh激活功能，而不是更受欢迎的ReLU。因为早在1998年，ReLU就没有被用于深度学习。使用tanh或sigmoid作为激活函数更为常见。 在今天实施LeNet时，通常将TANH换成RELU 。我们将遵循相同的指导原则，并在本章后面使用ReLU作为我们的激活功能。

       我们的输入层采用具有28行，28列和单个通道（灰度）的输入图像用于深度（即，MNIST数据集内的图像的尺寸）。 然后我们学习了20个滤波器，每个滤波器都是5×5。CONV层之后是ReLU激活，然后是2×2大小和步长s为2的最大池化。

        该架构的下一个块遵循相同的模式， 这次学习50个5×5滤波器。随着实际空间输入尺寸的减小，在网络的更深层中看到CONV层的数量增加是常见的。然后我们有两个FC层。 第一个FC包含500个隐藏节点，然后是ReLU激活。 最后的FC层控制输出类标签的数量（0-9;每个可能的十个数字一个）。 最后，我们应用softmax激活来获得分类概率。

二、LeNet的python实现部分

        使用Keras库实现开源的LeNet架构。 首先在pyimagesearch.nn.conv子模块中添加一个名为lenet.py的新文件 - 该文件将存储我们实际的LeNet实现：

        在lenet.py文件中，需要导入的包有：

from keras.models import Sequential
from keras.layers.convolutional import Convolution2D
from keras.layers.convolutional import MaxPooling2D
from keras.layers.core import Activation
from keras.layers.core import Flatten
from keras.layers.core import Dense

         初始化的参数有：

1. 输入图片的宽度
2. 输入图片的高度
3. 输入图片的通道数目
4. 分类任务中的分类标签数目

class LeNet:
    @staticmethod
    def build(width, height, depth, classes, weightsPath=None):
        # initialize the model
        model = Sequential()

        # first set of CONV => RELU => POOL
        model.add(Convolution2D(20, 5, 5, border_mode="same",
            input_shape=(depth, height, width)))
        model.add(Activation("relu"))
        model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))

        # second set of CONV => RELU => POOL
        model.add(Convolution2D(50, 5, 5, border_mode="same"))
        model.add(Activation("relu"))
        model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))

        # set of FC => RELU layers
        model.add(Flatten())
        model.add(Dense(500))
        model.add(Activation("relu"))

        # softmax classifier
        model.add(Dense(classes))
        model.add(Activation("softmax"))

        # if weightsPath is specified load the weights
        if weightsPath is not None:
            model.load_weights(weightsPath)

        return model

       第一组的CONV => RELU => POOL定义为：

# first set of CONV => RELU => POOL
        model.add(Convolution2D(20, 5, 5, border_mode="same", input_shape=(depth, height, width)))
        model.add(Activation("relu"))
        model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))

       这时，卷积层将会用20个每个大小为5×5的滤波器。然后，我们将用一个ReLu激活函数，然后，使用一个2×2大小、2×2步长的池化操作。这样输入图片的大小可以减少75%。

        另一个CONV => RELU => POOL定义为：

# second set of CONV => RELU => POOL
        model.add(Convolution2D(50, 5, 5, border_mode="same"))
        model.add(Activation("relu"))
        model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))

       这时，卷积层会使用50个每个大小为5×5的滤波器。然后，我们将用一个ReLu激活函数，然后使用一个2×2大小、2×2步长的池化操作。

       然后，就会有一个平整化（flattened）与一个有500个神经元节点的全连接层：

 # set of FC => RELU layers
        model.add(Flatten())
        model.add(Dense(500))
        model.add(Activation("relu"))

        最后，就是最终用softmax激活函数进行分类：

# softmax classifier
        model.add(Dense(classes))
        model.add(Activation("softmax"))

       好啦，现在已经编写了LeNet架构，我们可以继续将其应用于下面的MNIST数据集。

三、LeNet on MNIST

        我们的下一步是创建一个负责以下内容的驱动程序脚本：

1. 从磁盘加载MNIST数据集。
2. 实例化LeNet架构。
3. 训练LeNet。
4. 评估网络性能。

       要在MNIST上训练和评估LeNet，请创建一个名为lenet_mnist.py的新文件，并且导入如下的包：

from keras.optimizers import SGD
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn import datasets
from keras import backend as K
import matplotlib.pyplot as plt
import numpy as np

        当然，需要导入的有：

• 1.我们要训练的网络架构。
• 2.训练网络的优化器（在本例中为SGD）。
• 3.一组（一组）便利函数，用于构建训练和测试给定的分裂
• 数据集。
• 4.计算分类回馈的功能函数，以便我们评估分类器的性能。

print("[INFP] accessing MNIST...")
# 从磁盘加载MNIST数据集
dataset=datasets.fetch_mldata("MNIST Original")
data=datasets.data

        dataset = datasets.fetch_mldata("MNIST Original")是从磁盘加载MNIST数据集。 如果这是第一次使用“MNIST Original”字符串调用fetch_mldata函数，则需要从mldata.org数据集存储库下载MNIST数据集。

        MNIST数据集被序列化为单个55MB文件，因此根据互联网连接，此下载可能需要几秒钟到几分钟。重要的是要注意每个MNIST样本内部数据由784-表示 d×28×28灰度图像的矢量（即原始像素强度）。 因此，我们需要根据我们是使用“通道优先”还是“通道最后”排序来重塑数据矩阵：

# reshape the design matrix such that the matrix is:
# num_sample x depth x row x columns
if K.image_data_format()=="channels_first":
    data=data.reshape(data.shape[0],1,28,28)
#otherwise,we are using "channels last"ordering,so the design matrix shape should be:
else:
    data=data.reshape(data.shape[0],28,28,1)

        如果正在执行“通道优先”排序（第21行和第22行），则重新排列数据矩阵，使得样本数是矩阵中的第一个条目，单个通道作为第二个条目，后跟行数 和列（分别为28和28）。 否则，我们假设我们使用“最后通道”排序，在这种情况下，矩阵被重新排列为首先采样数，行数，列数，最后是通道数（第26和27行）。现在我们的数据 矩阵形状正确，我们可以执行训练和测试分割，注意将图像像素强度缩放到[0：1]范围：

# scale the input data to the range[0,1] and perform a train/test split
(trainX,testX,trainY,testY)=train_test_split(data/255.0,dataset.target.astype("int"),test_size=0.25,random_state=42)
# convert the labels from integers to vectors
le=LabelBinarizer()
trainY=le.fit_transform(trainY)
testY=le.transform(testY)

       在分割数据之后，我们还将类标签编码为单热矢量而不是单个整数值。 例如，如果给定样本的类标签是3，那么标签的单热编码输出将是：[0,0,0,1,0,0,0,0,0,0]
       注意向量中的所有条目除了第四个索引（现在设置为1）之外都是零（请记住，数字0是第一个索引，因此为什么三个是第四个索引）。现在阶段设置为训练LeNet 在MNIST上：

# initialize the optimizer and model
print("[INFO] compiling model...")
opt=SGD(lr=0.01)
model=LeNet.build(width=28,height=28,depth=1,classes=10)
model.compile(loss="categorical_crossentropy",optimizer=opt,metrics=["accuracy"])
# train the network
print("[INFO] training network...")
H=model.fit(trainX,trainY,validation_data=(testX,testY),batch_size=128,epochs=20,verbose=1)

        opt=SGD(lr=0.01) 初始化我们的SGD优化器，学习率为0.01。

        LeNet本身在model=LeNet.build(width=28,height=28,depth=1,classes=10)实例化，表明我们数据集中的所有输入图像都是28像素宽，28像素高，深度为1.鉴于MNIST数据集中有10个类（每个数字一个），0- 9），我们设置classes = 10.

        model.compile(loss="categorical_crossentropy",optimizer=opt,metrics=["accuracy"])使用交叉熵损失编译模型作为我们的损失函数。 H=model.fit(trainX,trainY,validation_data=(testX,testY),batch_size=128,epochs=20,verbose=1) 在MNIST上使用128的小批量训练LeNet共计20个时期。最后，我们可以评估我们网络的性能，并绘制下面最终代码块中的损失和准确性：

# evaluates the network
print("[INFO] evaluating network...")
predictions=model.predict(testX,batch_size=128)
print(classification_report(testY.argmax(axis=1),predictions.argmax(axis=1),target_names=[str(x) for x in le.classes_]))
# plot the training loss and accuracy
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0,20),H.history["loss"],label="train_loss")
plt.plot(np.arange(0,20),H.history["val_loss"],label="val_loss")
plt.plot(np.arange(0,20),H.history["acc"],label="train_acc")
plt.plot(np.arange(0,20),H.history["val_acc"],label="val_acc")
plt.title("Training Loss and Accuracy")
plt.legend()
plt.show()

        在评估ShallowNet时应理解了在调用model.predict时predictions=model.predict(testX,batch_size=128)正在做什么。 对于testX中的每个样本，构建大小为128的batch_size，然后通过网络进行分类。 在对所有测试数据点进行分类之后，返回预测变量。预测变量实际上是具有形状的NumPy数组（len（testX），10）意味着我们现在具有与每个数据的每个类标签相关联的10个概率 在testX中指出。 在第54-56行的classification_report中进行预测.argmax（axis = 1）查找具有最大概率的标签的索引（即最终输出分类）。从网络中给出最终分类，我们可以比较我们预测的标签类别与真值。要执行我们的脚本，只需发出以下命令：

python lenet_mnist.py

        然后，从磁盘下载（或加载）MNIST数据集，并开始培训：

 

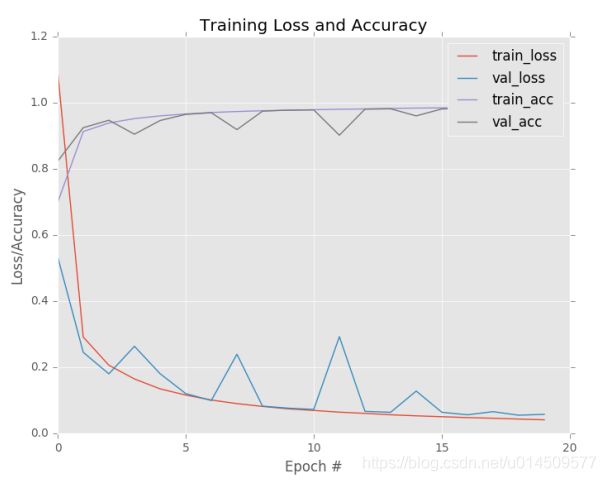
         训练结束后，可以看到LeNet正在获得98％的分类准确度，与第10章中使用标准前馈神经网络时的92％相比有很大的增长。此外，在下面的结果图中可以查看我们的损失和准确度曲线表明我们的网络表现得非常好。 仅仅五个时期之后，LeNet已达到≈96％的分类精度。 由于我们的学习速度保持不变而且没有衰减，训练和验证数据的损失继续下降，只有少数轻微的“峰值”。 在第二十世纪末，测试集的准确率达到98％。

                                       图1   在MNIST上训练LeNet。 在仅仅二十个时期之后，我们获得了98％的分类准确度。

        这个图表证明了LeNet在MNIST上的损失和准确性可以说是我们正在寻找的典型图：训练和验证损失和准确性相互模拟（几乎）完全没有过度拟合的迹象。正如我们所看到的，通常很难获得这种行为非常好的训练图，表明我们的网络正在学习基础模式而不会过度拟合。

        还存在MNIST数据集经过大量预处理并且不能代表我们在现实世界中遇到的图像分类问题的问题。研究人员倾向于使用MNIST数据集作为评估新分类算法的基准。如果他们的方法不能获得> 95％的分类准确度，那么（1）算法的逻辑或（2）实现本身存在缺陷。尽管如此，将LeNet应用于MNIST是一种很好的方式来获得您的第一次尝试深入学习图像分类问题并模仿开创性的LeCun等人的论文。

四、总结

        在本章中，我们探讨了LeCun等人介绍的LeNet架构。在1998年的论文中，基于梯度的学习应用于文档识别[19]。 LeNet是深度学习文献中的一项开创性工作。它展示了​​如何以端到端的方式训练神经网络用来识别图像中的对象（即，不必进行特征提取，网络能够学习来自图像本身的模式）。

        虽然具有开创性，但LeNet按今天的标准仍被视为“浅层”网络。只有四个可训练层（两个CONV层和两个FC层），与当前最先进的架构（如VGG（16和19层）和ResNet（100+层）的深度相比，LeNet的深度相形见绌。

      在讨论VGGNet架构的一种变体，称之为“MiniVGGNet”。这种架构的变化使用与Simonyan和Zisserman的工作完全相同的指导原则[95]，但减少了深度，使我们能够在较小的数据集上训练网络。要完全实现VGGNet体系结构，需要参考 ImageNet Bundle，并在ImageNet上从头开始训练VGGNet。