数据结构-<栈和队列>
文章目录
- 栈
-
- 定义引入
- 栈的定义
- 有关栈的细节
- 栈操作
-
- 栈的初始化
- 初始化空栈
- 删除栈
- 入栈
- 出栈
- 链栈
-
- 创建一个链栈`
- 链式入栈
- 链式出栈
- 栈的思想应用-括号匹配问题
- 循环队列
-
- 定义
- 循环队列的思考
- 解决
- 队列操作
- 队列思想的应用——旋转数组
-
- 思路
- 代码
栈
定义引入
.在给玩具枪上子弹的时候,我们的操作是掏出弹匣,依次从底部把子弹送入弹匣内我们要是想让弹匣变空就会把子弹一个一个取出来,仔细的人或许知道先放进去的最后才能取出,这种先进后出就是栈的一种体现
栈的定义
1.栈(stack)是限定仅允许在表尾进行插入和删除操作的线性表。
2.我们把允许插入和删除的一边称为栈顶(top),另一端称为栈底。
不含有任何元素的栈叫空栈。
栈具有LIFO结构----先进后出。
有关栈的细节
1.首先它是一个线性表,也就是说,栈元素具有线性关系,即前驱后继关系。
2.只过它是一种特殊的线性表而已。定义中说是在线性表的表尾进行插人和删除操作,这里表尾是指栈顶,而不是栈底。
它的特殊之处就在于限制了这个线性表的插人和删除位置,它始终只在栈顶进
这也就使得:栈底是固定的,最先进栈的只能在栈底。
3.栈的插入操作,叫作进栈,也称压栈、入栈。类似子弹入弹夹。
4栈的删除操作,叫作出栈,也有的叫作弹栈。如同弹夹中的子弹出夹
栈操作
栈的初始化
<由于栈的特性我们采取结构体的方法创建一个栈>
typedef struct {
int stacksize;//栈可用的最大容量
int *top;//栈顶指针,注意=栈顶指针总是在栈顶元素的下一位,方便计算
int *base;//栈底指针
} sqstack;//顺序栈
sqstack *S
####关于初始化
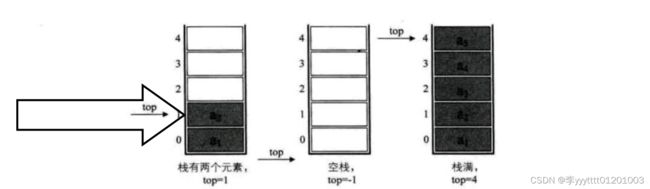
1.top 指针变量来指示栈顶元素在数组中的位置,这top 就如同箭头,意味着栈顶的 top可以移动,但无论如何top不能超出栈的长度。若存储栈的长度为 Stacksize . 栈顶位置top 必须小于 StackSize。
2.当栈存在一个元素时,top 等于 0,因此通常把栈空的判定条件定为top 等于-1。
初始化空栈
首先我们要知道栈为空的时候栈顶指针等于栈底指针即S->top == S->base;
//初始化空栈
void initstack(sqstack *S, int n) {
S->base = (int*)malloc(sizeof(n));
if(!S->base) {
exit(0);
}
S->stacksize = n;
S->top = S->base;
}
```c
//当top=base的时候,此时的栈顶等于栈底,栈自然就和清空了
//清空栈
void clearstack(sqstack *S) {
S->top = S->base;//线性表不是链表我们直接让top=base;中间的元素就消除了
}
删除栈
//销毁栈
void deletestack(sqstack *S) {
if(S->base) { //栈存在
S->stacksize = 0;
S->top = S->base = NULL;
}
}
入栈
正常情况下入栈前进行栈是否已经满进行判断(s->top == s-> base)
void pushstack(sqstack *S, int e) {
//判断栈满
if(S->top - S->base == S->stacksize) {
printf("栈满");
} else {
*S->top = e;//先赋值,top向上走1个位置
S->top++;//*S->top++=e;
}
}
出栈
//顺序出栈
void stackpop(sqstack*S, int e) {
if(S->top == S->base) {
printf("栈空"); //栈空,无法返回元素
} else {
e = *--S->top; //因为top是栈顶元素的下一个位置,所以该语句=*S->top--;e=S->top;
}
}
链栈
定义:栈的链式存储结构,我们知道栈是对top指针进行操作的,那么链栈就是将栈的
top指针变成了head头指针,合二为一,也就是对于链栈来说是不需要头节点的;
- 对于空栈来说,栈的top指针=NULL
创建一个链栈`
typedef struct StackNode {
int data; //存放栈的数据
struct StackNode *next;
} StackNode, *LinkStackPtr;
typedef struct LinkStack1 {
LinkStackPtr top; //top指针
int count; // 栈元素计数器
} LinkStack;
链栈的操作是建立单链表的前提下完成的,下面展示插入和删除上一些不同的地方
`
链式入栈
int StatusPush(LinkStack *s, int e) {
LinkStackPtr p = (LinkStackPtr)malloc(sizeof(StackNode));
p->data = e;
p->next = s->top;//前栈顶元素直接复赋值给新节点的直接后继//
s->top = p;
s->count++;
return 1;
}
链式出栈
int StatusPop(LinkStack *s, int *e) {
LinkStackPtr p;
*e = s->top->data;
p = s->top;
s->top = s->top->next;
free(p);
s->count--;
return 1;
}
对比一下顺序栈与链栈,它们在时间复杂度上是一样的,均为 0(1)。对于空间性能,顺序栈需要事先确定几个固定的长度,可能会存在内存空问浪费的问题:
优势是存取时定位很方便,而链栈则要求每个元素都有指针域,这同时也增加了内存开销,但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样
•如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈
栈的思想应用-括号匹配问题
//#include循环队列
定义
队列是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
我们把允许插入的一端称队伍尾巴,进行删除操作的一端称为队头
为了防止队列的溢出我们一般创建的是循环队列;
为了避免只有一个元素时,了头和队尾重合使处理变得麻烦,所以引入两个指镇行ront 指针指安队头元素,
rear 指针指向队尾元素的下一个位置,这样当 front 等于rear时,此队列不是还剩一个元素,而是空队列。
循环队列的思考
此时问题叉出来了,我们刚才说,空队列时,front 等于rear,现在当队列满
时,也是front 等于reat,那么如何判断此时的队列究竟是空还是满呢?
办法一是设置一个标志变量 Aag, 当front == teat, 且flag= 0时为队列空,
当front == reat,且 fag=1时为队列满。
•办法二是当队列空时,条件就是 front
=teat,当队列满时,我们修改其条
件,保留一个元素空间。也就是说,队列满时,数组中还有一个室闲单元。
我们就认为此队列已经满了,也就是说,我们队列中没有空的格子出现
解决
因此我们判断队列是否已经全部填满的条件就是 (rear+1)%QSIZE == front;
通用的计算队列的长度公式 (rear-fonrt+qsiez)%qsize;
队列操作
通过以上的简单细节问题我们现在开始进行队列的一些基本操作
#include要掌握队列就要先看懂细节问题,循环队列是怎样判断队满还是队空的
如果front或者rear到了队伍的最后这样就变到前面去了这都是值得思考的问题
队列思想的应用——旋转数组
思路
思考:我们已经知道了要旋转k次,现在开辟一个数组把我们把我们这个数组的元素一次放进去,之后我们光给下标加k是不行的,这存在很明显的越界问题,这个时候就想到了刚才循环队列的思想,我们知道了数组的长度SIZE我们的元素存放的位置就是(i(当前下标)+k )%SIZE;
代码
void rotate(int* nums, int numsSize, int k) {
int nums1[numsSize], i;
for(i = 0; i < numsSize; i++) {
nums1[i] = nums[i];
}
for(i=0; i < numsSize; i++) {
nums[(i+k) % numsSize] = nums1[i];
}
return nums;
}
2022-4-28