1.Summary:
Apply the chain rule to compute the gradient of the loss function with respect to the inputs.
----cs231n
2.what problems to slove?
2.1introduction
神经网络的本质是一个多层的复合函数,图:

表达式为:

上面式中的Wij就是相邻两层神经元之间的权值,它们就是深度学习需要学习的参数,也就相当于直线拟合y=k*x+b中的待求参数k和b。
和直线拟合一样,深度学习的训练也有一个目标函数,这个目标函数定义了什么样的参数才算一组“好参数”,不过在机器学习中,一般是采用成本函数(cost function),然后,训练目标就是通过调整每一个权值Wij来使得cost达到最小。cost函数也可以看成是由所有待求权值Wij为自变量的复合函数,而且基本上是非凸的,即含有许多局部最小值。但实际中发现,采用我们常用的梯度下降法就可以有效的求解最小化cost函数的问题。
梯度下降法需要给定一个初始点,并求出该点的梯度向量,然后以负梯度方向为搜索方向,以一定的步长进行搜索,从而确定下一个迭代点,再计算该新的梯度方向,如此重复直到cost收敛。那么如何计算梯度呢?
假设我们把cost函数表示为, 那么它的梯度向量就等于, 其中表示正交单位向量。为此,我们需求出cost函数H对每一个权值Wij的偏导数。而BP算法正是用来求解这种多层复合函数的所有变量的偏导数的利器。
2.2processing (an example)
以求e=(a+b)*(b+1)的偏导为例。
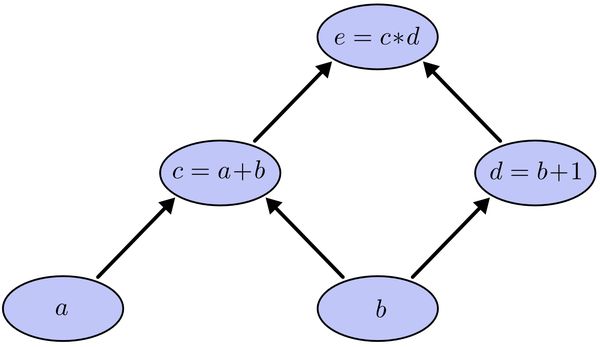
为了求出a=2, b=1时,e的梯度,我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系,如下图所示。
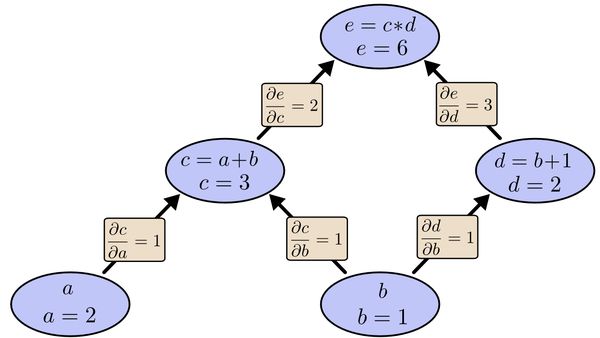
利用链式法则我们知道:
 以及
以及
链式法则在上图中的意义是什么呢?其实不难发现,的值等于从a到e的路径上的偏导值的乘积,而的值等于从b到e的路径1(b-c-e)上的偏导值的乘积加上路径2(b-d-e)上的偏导值的乘积。也就是说,对于上层节点p和下层节点q,要求得,需要找到从q节点到p节点的所有路径,并且对每条路径,求得该路径上的所有偏导数之乘积,然后将所有路径的 “乘积” 累加起来才能得到的值。大家也许已经注意到,这样做是十分冗余的,因为很多路径被重复访问了。比如上图中,a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络,这样的冗余所导致的计算量是相当大的。
同样是利用链式法则,BP算法则机智地避开了这种冗余,它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
正如反向传播(BP)算法的名字说的那样,BP算法是反向(自上往下)来寻找路径的。
从最上层的节点e开始,初始值为1,以层为单位进行处理。对于e的下一层的所有子节点,将1乘以e到某个节点路径上的偏导值,并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后,第二层的每一个节点都“堆放"些值,然后我们针对每个节点,把它里面所有“堆放”的值求和,就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点,初始值设为顶点e对它们的偏导值,以"层"为单位重复上述传播过程,即可求出顶点e对每一层节点的偏导数。
以上图为例,节点c接受e发送的1*2并堆放起来,节点d接受e发送的1*3并堆放起来,至此第二层完毕,求出各节点总堆放量并继续向下一层发送。节点
c向a发送2*1并对堆放起来,节点c向b发送2*1并堆放起来,节点d向b发送3*1并堆放起来,至此第三层完毕,节点a堆放起来的量为2,节点b堆放起来
的量为2*1+3*1=5, 即顶点e对b的偏导数为5.
引用:
【作者:匿名用户
链接:https://www.zhihu.com/question/27239198/answer/89853077
来源:知乎
著作权归作者所有,转载请联系作者获得授权。】
3.3-layer 神经网络
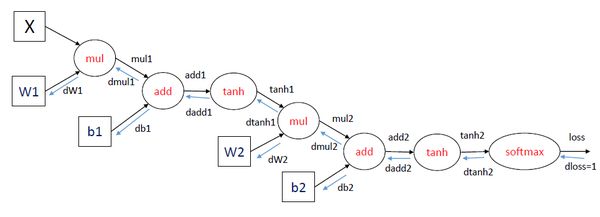
这里举了一个三层神经网络(一个输入层、一个隐层和一个输出层)的例子,使用了softmax输出层,损失函数使用交叉熵。训练神经网络可以使用梯度下降的方法,重点是计算梯度,也就是损失函数对参数的导数,在图中可以表示为dloss/dW1,dloss/dW2,dloss/db1和dloss/db2。如何计算这些梯度,使用的就是BP算法,其实也就是求导的链式法则。
在每一轮迭代中,首先进行forward propagation,也就是计算computation graph中每个节点的状态:
mul1 = X * W1
add1 = mul1 + b1
tanh1 = tanh(add1)
mul2 = tanh1 * W2
add2 = mul2 + b2
tanh2 = tanh(add2)
loss = softmax_loss(tanh2)
之后进行back propagation,也就是计算computation graph中每个节点相对于损失函数(这里表示为loss)的导数,这里面应用了链式法则。对于dloss/dtanh2, dloss/dadd2等导数,下面省略分子直接表示为dtanh2等。
dloss = 1
dtanh2 = softmax_loss_diff(tanh2) * dloss
dadd2 = tanh_diff(add2) * dtanh2
db2 = 1 * dadd2
dmul2 = 1 * dadd2
dW2 = tanh1 * dmul2
dtanh1 = W2 * dmul2
dadd1 = tanh_diff(add1) * dtanh1
db1 = 1 * dadd1
dmul1 = 1 * dadd1
dW1 = X * dmul1
上面的变量都可以用矩阵表示,直接进行矩阵运算。其中dW1,dW2,db1和db2就是我们需要求的参数的梯度。
在编程实现上,每一个计算节点都可以定义两个函数,一个是forward,用于给定输入计算输出;一个是backward,用于给定反向梯度,计算整个表达式(相当于损失函数)相对于这个节点的输入的梯度, 应用链式法则就是:这个节点相对于其输入的梯度(直接对输入求导)乘以这个节点接受的反向梯度。
作者:龚禹pangolulu
链接:https://www.zhihu.com/question/27239198/answer/95253534
来源:知乎
著作权归作者所有,转载请联系作者获得授权。




