Andrew Ng吴恩达深度学习Course_1笔记

基于吴恩达深度学习课程所记的相关笔记

术语概念

NN： Neural Network神经网络

ReLU函数：修正线性单元

sigmoid函数：$\sigma (z)$ = $\frac{1}{1+e^{-z}}$

SIMD：单指令多数据流

broadcasting：在python中使用numpy进行按位运算的时候，有一个小技巧可以帮助减少代码量——那就是broadcasting,广播机制。 简单来说，broadcasting可以这样理解：如果你有一个m * n的矩阵，让它加减乘除一个1 * n的矩阵，它会被复制m次，成为一个m * n的矩阵，然后再逐元素地进行加减乘除操作。同样地对m * 1的矩阵成立。行和列至少要有一个匹配。比如一个4 * 3的矩阵和一个3 * 2的矩阵相乘，就不能用broadcasting，只能用numpy. dot。

m:训练集规模

增大训练集大小不会对算法性能产生影响，反而可能有很大帮助；减小神经网络规模或许性能会更好。

成本函数cost function：$J=\frac{1}{m}{\sum }_{i=1}^{m}L(a^{(i)},y^{(i)})$

前向/后向传播forward/backward：
$$\begin{gathered} A=\sigma (w^{T}X+b)=(a^{(i)},a^{(2)},...,a^{(m-1)},a^{(m)}) \\ J=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}log(a^{(i)})+(1-y^{(i)})log(1-a^{(i)})) \\ \frac{\partial J}{\partial w}=\frac{1}{m}X(A-Y{)}^T \\ \frac{\partial J}{\partial b}=\frac{1}{m}\sum _{i=1}^m(a^{(i)}-y^{(i)}) \end{gathered}$$
隐藏层hidden layer：除输入层和输出层以外的其他各层叫做隐藏层，可以理解为神经网络中间的黑盒子

1. 每个隐藏层都可以应用您想要的任何函数到前一层（通常是线性变换，然后是压缩非线性）。
2. 隐藏层的工作是将输入转换为输出层可以使用的东西。
3. 输出层将隐藏层激活转换为您希望输出所在的任何比例

第一周 深度学习概念

略

第二周 神经网络基础

Notation

x：将训练样本按列排列的数据量，m等于样本总数

logistic回归函数

最终概率 $\hat{y}$ 逼近于y（当y=1时， $\hat{y}$ 逼近1），而非无穷大，因此在线性回归函数之外套一个$\sigma$(z)公式；

主要研究w和b（相当于原本线性回归里的斜率k和截距b）

Loss function损失函数和Cost function成本函数

Loss function损失函数： y与$\hat{y}$之间的差值越小越好，即当y=1时， $\hat{y}$就尽量大，当y=0时， $\hat{y}$ 尽量小，仅用于单个训练样本，衡量了在单个训练样本上的表现（每个分段都可能出现局部最优解）

Cost function成本函数：衡量在总体训练样本上的表现，找到合适的w和b，使得 J (w,b) 最小

梯度下降法

每次迭代选择坡度最陡的方向下降一步，当只有一个参数（w或b）时，即用导数，参数大于等于2时，用偏导数

logistics回归中的梯度下降法

利用链式求导（单个训练样本）

$\alpha$ 指学习率

神经元先进行线性计算($z=w^{T}X+b$)，然后激活函数 (sigmoid, ReLU, …)

m个样本的梯度下降：有两个for循环（绿字），可以用向量化（即矩阵运算）来摆脱显式 for循环，一次性计算多个值，运算速度大幅上升

向量化logistics回归

只需一行代码

z = np.dot(w.T, X) + b
#w.T是w的转置矩阵

注意：编程时少用秩为1的数组，行、列不明确，行为不好预测，易产生bug

assert（）声明确保是一个向量，如果遇到秩为1的数组，可以使用reshape（）将其化为向量

reshape((2, -1))中的-1被理解为为unspecified value，意思是未指定为给定的。如果我只需要特定的行数，列数多少我无所谓，我只需要指定行数，那么列数直接用-1代替就行了，计算机帮我们算赢有多少列，反之亦然。

A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b ∗ c ∗ d, a) is to use:

X_flatten = X.reshape(X.shape[0], -1).T      # X.T is the transpose of X
#相当于指定a列，每列长度为b*c*d，长度为计算机算出

损失函数cost（optional）

简单神经网络——判断图上是否是猫

设图片的大小为64 * 64，格式为RGB，即三个颜色通道，则image .size=64643=12288

For one example () :
KaTeX parse error: Expected 'EOF', got '&' at position 151: …og(1−^{()})&̲\quad\quad\quad…
The cost is then computed by summing over all training examples:
$$J=\frac{1}{m}\sum _{i=1}^{m}L(a^{(i)},y^{(i)})$$

Forward and Backward Propagation:

w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)

$$\begin{gathered} A=\sigma (w^{T}X+b)=(a^{(i)},a^{(2)},...,a^{(m-1)},a^{(m)}) \\ J=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}log(a^{(i)})+(1-y^{(i)})log(1-a^{(i)})) \\ \frac{\partial J}{\partial w}=\frac{1}{m}X(A-Y{)}^T \\ \frac{\partial J}{\partial b}=\frac{1}{m}\sum _{i=1}^m(a^{(i)}-y^{(i)}) \end{gathered}$$

logistics回归图片识别流程图（以识别猫为例）

• train_set_x_orig ：保存的是训练集里面的图像数据（本训练集有209张64x64的图像）。
• train_set_y_orig ：保存的是训练集的图像对应的分类值（【0 | 1】，0表示不是猫，1表示是猫）。
• test_set_x_orig ：保存的是测试集里面的图像数据（本训练集有50张64x64的图像）。
• test_set_y_orig ： 保存的是测试集的图像对应的分类值（【0 | 1】，0表示不是猫，1表示是猫）。

第三周 浅层神经网络

Hidden layer隐藏层

会产生激活值，但训练中无法看到

图中是一个双层神经网络2 layer NN，隐藏层是第一层，输出层是第二层，输入层为第零层不看作一个i标准的层

隐藏节点

多个例子的向量化

[]->layer,()->example

向量化实现的矩阵表示

令b=0简化描述，注意[]和()不同

$X=A^{[0]}$

激活函数

激活函数常用g()表示，常见的激活函数：

sigmoid（σ）,

tanh(σ的平移版本，输出介于-1和1之间，效果更好)，

ReLU(线性修正，如今常用)

Leaky ReLU（带泄露的ReLU，a = max(0.01 z, z))

……

如果没有非线性激活函数，神经网络就失去了意义。因为神经网络就是模仿人的神经元，而人的神经元只有在接受的刺激达到一定程度时才会产生电信号，线性函数不能反映刺激的剧烈程度，即导数恒定。唯一可以用线性激活函数的地方通常在输出层，除此之外会在隐层用线性的可能与压缩有关。（ReLU不是线性函数）

激活函数的导数

sigmoid:
$$\begin{gathered} g(z)=\frac{1}{1+e^{-z}} \\ {g}^{\prime }(z)=g(z)(1-g(z))=a(1-a) \end{gathered}$$

tanh:
$$\begin{gathered} g(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} \\ {g}^{\prime }(z)=1-g(z{)}^2=1-a^2 \end{gathered}$$

ReLU and Leaky ReLU:
$$\begin{gathered} g(z)=max(0,z)g(z)=max(0.01z,z) \\ {g}^{\prime }(z)=\{\begin{array}{l}0,z<0\\ 1,z\ge 0\end{array}{g}^{\prime }(z)=\{\begin{array}{l}0.01,z<0\\ 1,z\ge 0\end{array} \end{gathered}$$

神经网络的梯度下降算法

$$\begin{gathered} parameters:w^{[1]},b^{[1]},w^{[2]},b^{[2]} \\ costfunction:J=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}log(a^{[2](i)}+(1-y^{(i)})log(1-a^{[2](i)}))) \\ gradientdescent:repeat\to \{\begin{array}{l}computepredict({\hat{y}}^{(i)},i=1,...,m)\\ d{w}^{[1]}=\frac{\partial J}{\partial w^{[1]}},d{b}^{[1]}=\frac{\partial J}{\partial b^{[1]}},...\\ w^{[1]}=w^{[1]}-\alpha d{w}^{[1]}\\ b^{[1]}=b^{[1]}-\alpha d{b}^{[1]}\\ w^{[2]}=...,b^{[2]}=...\end{array} \\ forwardpropagate:z^{[i]}=w^{[i]}X+b^{[i]},A^{[i]}=g^{[i]}(z^{[i]}) \\ {z}^{[i+1]}=w^{[i+1]}A![i]+b^{[i+1]},... \\ backpropagate:d{z}^{[i]}=A^{[i]}-Y,d{w}^{[i]}=\frac{1}{m}d{z}^{[i]}{A}^{[i]T}, \\ d{b}^{[i]}=\frac{1}{m}np.sum(d{z}^{[i]},axis=1,keepdims=True) \end{gathered}$$

梯度下降公式总结：

随机初始化

完全对称：当w初始参数全为0时，两个隐藏单元计算完全一样的函数，结果相同， 梯度下降法无效。

解决方案：初始化参数随机

w=np.random.randn((2,2))*0.01	#选择0.01，防止w过大，tanh，sigmoid类激活函数接近饱和减缓学习速度
b=np.zero((2,1))	#b初始化为0没有问题

构建神经网络的一般方法

第四周 深层神经网络

deep neural network

只有深层的神经网络在学习中好用

深层网络中的前向传播

forward propagate:需要使用显示for循环
$$\begin{gathered} z^{[i]}=w^{[i]}X+b^{[i]},A^{[i]}=g^{[i]}(z^{[i]}) \\ {z}^{[i+1]}=w^{[i+1]}{A}^{[i]}+b^{[i+1]},A^{[i+1]}=g^{[i+1]}(z^{[i+1]}) \\ ... \end{gathered}$$

核对矩阵维数

debug时常用的方法，矩阵的维度需要谨慎核对，易出现bug

w和dw的维度相同，b和db的维度相同，做反向传播时，一定要确认所有的矩阵维数是前后一致的
$$\begin{gathered} w^{[l]}:(n^{[l]},n^{[l-1]}) \\ {b}^{[l]}:(n^{[l]},1) \end{gathered}$$

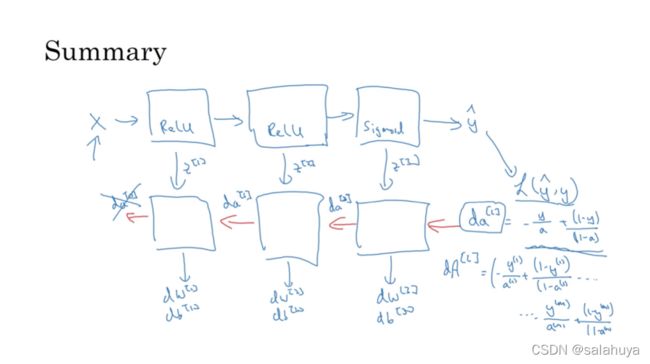
深层神经网络的构建

正向传播：输入a[l-1]，输出a[l]，以及输出到缓存的z[l]，w[l]，b[l]（用于后续计算反向函数）；

反向传播：输入da[l]，输出da[l-1]，用到w，b，计算dz，最终输出dw[l]，db[l]（红色为反向）

这张图非常好，思路总结，值得一看：

前向和反向传播

前向传播有三个步骤：

• LINEAR
• LINEAR - >ACTIVATION，其中激活函数将会使用ReLU或Sigmoid。
• [LINEAR - > RELU] ×（L-1） - > LINEAR - > SIGMOID（整个模型）

公式：

$z^{[i+1]}=w^{[i+1]}{A}^{[i]}+b^{[i+1]}$

$$\begin{gathered} d{w}^{[l]}=\frac{\partial J}{\partial w^{[l]}}=\frac{1}{m}d{Z}^{[l]}{A}^{[l-1]T} \\ d{b}^{[l]}=\frac{\partial J}{\partial b^{[l]}}=\frac{1}{m}\sum _{i=1}^{m}d{Z}^{[l](i)} \\ d{A}^{[l-1]}=\frac{\partial J}{\partial A^{[l-1]}}=W^{[l]T}d{Z}^{[l]} \end{gathered}$$

$$\begin{gathered} d{a}^{[l]}=-\frac{y}{a}+\frac{(1-y)}{(1-a)} \\ d{A}^{[l]}=-\frac{y^{[1]}}{a^{[1]}}+\frac{(1-y^{[1]})}{(1-a^{[1]})}+...-\frac{y^{[m]}}{a^{[m]}}+\frac{(1-y^{[m]})}{(1-a^{[m]})} \end{gathered}$$

参数和超参数

超参数能够控制w,b（参数），即参数的参数，深度学习有大量的超参数

更新参数公式：

$$\begin{gathered} W^{[l]}=W^{[l]}-\alpha d{W}^{[l]} \\ {b}^{[l]}=b^{[l]}-\alpha d{b}^{[l]} \end{gathered}$$

其中α是学习率

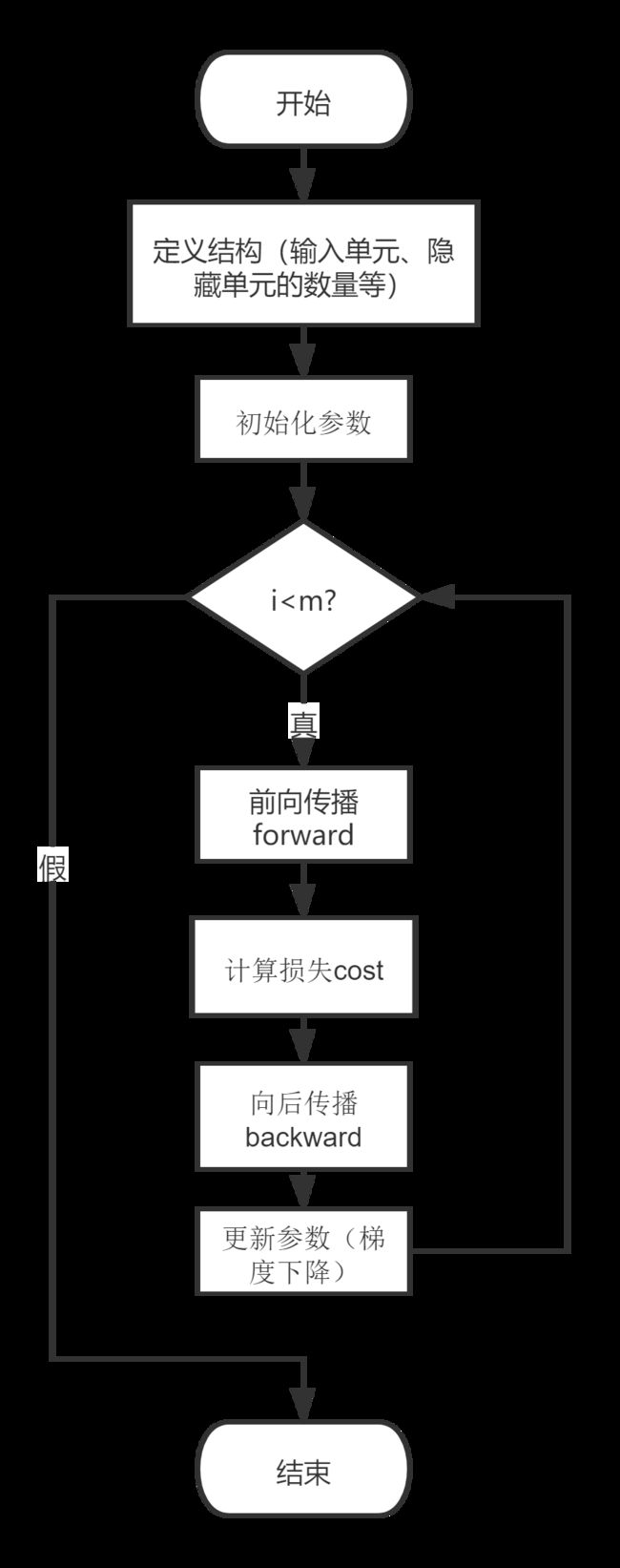
构造深层网络及应用

基本步骤

1.初始化网络参数

2.前向传播

​ 2.1 计算一层的中线性求和的部分

​ 2.2 计算激活函数的部分（ReLU使用L-1次，Sigmod使用1次）

​ 2.3 结合线性求和与激活函数

3.计算误差

4.反向传播

​ 4.1 线性部分的反向传播公式

​ 4.2 激活函数部分的反向传播公式

​ 4.3 结合线性部分与激活函数的反向传播公式

5.更新参数

注意：对于每个前向函数，都有一个相应的后向函数。 这就是为什么在我们的转发模块的每一步都会在cache中存储一些值，cache的值对计算梯度很有用， 在反向传播模块中，我们将使用cache来计算梯度。

课后作业

https://download.csdn.net/download/weixin_44163570/57108022