国科大模式识别导论作业2:Parzen窗估计
目录
- 题目
- 代码:方窗
-
- 方窗结果
- 代码:高斯窗
-
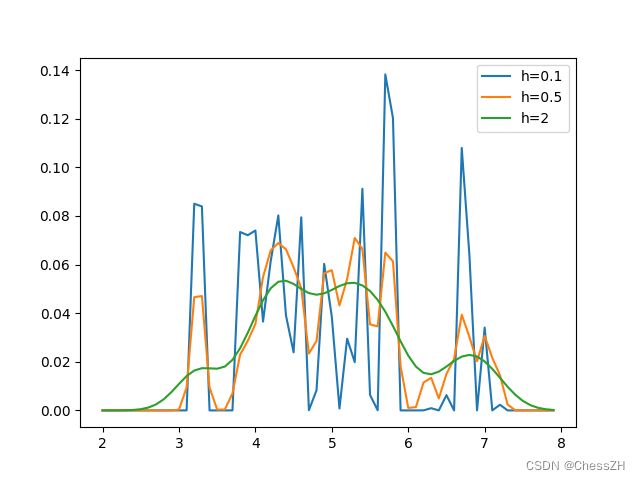
- 高斯窗结果
很久没写博客了,更新一下近期作业里的编程题
题目
现有一维空间的 50 个样本点(实际上,这些样本点是在 Matlab 中按如下语句生成的:mu=5; std_var = 1; X=mvnrnd(mu, std_var, 50);)。现需要采用 Parzen 窗方法对概率密度函数进行估计。请分别编程实现方窗和高斯窗情形下的概率密度函数估计;请讨论窗宽的影响,并画出几种不同窗宽取值下所估计获得的概率密度函数曲线。50 样本点如下:

代码:方窗
# 现有一维空间的 50 个样本点(实际上,这些样本点是在 Matlab 中按如下语句生成的:
# mu=5; std_var = 1; X=mvnrnd(mu, std_var, 50);)。现需要采用 Parzen 窗方法对概率密度函
# 数进行估计。请分别编程实现方窗和高斯窗情形下的概率密度函数估计;请讨论窗宽的
# 影响,并画出几种不同窗宽取值下所估计获得的概率密度函数曲线。50 样本点如下
import numpy as np
import matplotlib.pyplot as plt
sample = [4.6019, 5.2564, 5.2200, 3.2886, 3.7942,
3.2271, 4.9275, 3.2789, 5.7019, 3.9945,
3.8936, 6.7906, 7.1624, 4.1807, 4.9630,
6.9630, 4.4597, 6.7175, 5.8198, 5.0555,
4.6469, 6.6931, 5.7111, 4.3672, 5.3927,
4.1220, 5.1489, 6.5319, 5.5318, 4.2403,
5.3480, 4.3022, 7.0193, 3.2063, 4.3405,
5.7715, 4.1797, 5.0179, 5.6545, 6.2577,
4.0729, 4.8301, 4.5283, 4.8858, 5.3695,
4.3814, 5.8001, 5.4267, 4.5277, 5.2760]
# print(sample.__len__())
# x值
X = [_ for _ in np.arange(2, 8, 0.1)]
# 方窗,窗宽为h
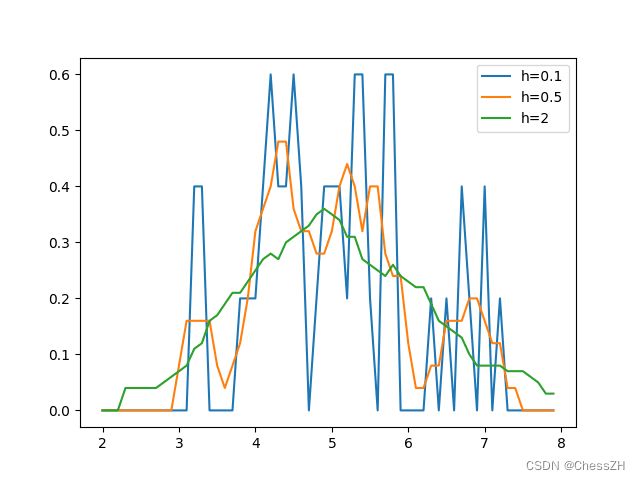
def Y_square(h):
Y = [0 for _ in X]
a = 1 / (h * 50)
for sample1 in sample:
for i in range(len(X)):
if abs(X[i] - sample1) < (h / 2):
Y[i] += a
return Y
y1 = Y_square(0.1)
y2 = Y_square(0.5)
y3 = Y_square(2)
# print(len(X),len(Y_square))
plt.plot(X, y1, label="h=0.1")
plt.plot(X, y2, label="h=0.5")
plt.plot(X, y3, label="h=2")
plt.legend()
plt.show()
方窗结果
代码:高斯窗
# 高斯窗计算
import numpy as np
import matplotlib.pyplot as plt
sample = [4.6019, 5.2564, 5.2200, 3.2886, 3.7942,
3.2271, 4.9275, 3.2789, 5.7019, 3.9945,
3.8936, 6.7906, 7.1624, 4.1807, 4.9630,
6.9630, 4.4597, 6.7175, 5.8198, 5.0555,
4.6469, 6.6931, 5.7111, 4.3672, 5.3927,
4.1220, 5.1489, 6.5319, 5.5318, 4.2403,
5.3480, 4.3022, 7.0193, 3.2063, 4.3405,
5.7715, 4.1797, 5.0179, 5.6545, 6.2577,
4.0729, 4.8301, 4.5283, 4.8858, 5.3695,
4.3814, 5.8001, 5.4267, 4.5277, 5.2760]
# print(sample.__len__())
# x值
X = [_ for _ in np.arange(2, 8, 0.1)]
# 高斯窗,窗宽为h
def Y_normal(h):
Y = [0 for _ in X]
hn = h / (50 ** 0.5)
for sample1 in sample:
for i in range(len(X)):
u = (sample1 - X[i]) / hn
fai = np.exp((-0.5) * u * u) / (6.28 ** 0.5)
Y[i] += fai / (50 * h)
return Y
y1 = Y_normal(0.1)
y2 = Y_normal(0.5)
y3 = Y_normal(2)
# print(len(X), len(y1))
plt.plot(X, y1, label="h=0.1")
plt.plot(X, y2, label="h=0.5")
plt.plot(X, y3, label="h=2")
plt.legend()
plt.show()