基于深度学习KNN的基于RSSI的室内定位系统仿真与实现

一.题目要求

基于深度学习的基于RSSI的室内定位系统仿真与实现

1.利用一种深度学习方法，基于蓝牙RSSI信息，实现定位位置的估计与预测。

2.数据来源：互联网上有一种公开RSSI数据集。

3.图形化显示定位结果并记录误差分析。

4.探讨分析如何进一步提高定位精度。

二.概要设计

1.核心方法介绍：KNN（K-最近邻算法）

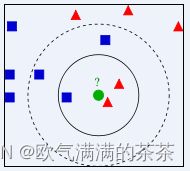
   KNN算法全称是K-最近邻算法，英文名称是K-Nearest Neighbor，简称为KNN；从算法名称上，可以猜出，是找到最近的k个邻居，在选取到的k个样本中选取出最近的且占比最高的类别作为预测类别。如下图所示：

 

上图所指示，蓝色的正方形和红色的三角形是已经存在的样本，而绿色的圆（待测样本）是要被赋予为那种类别，即是红色的三角形还是蓝色的正方形。如果取k=3，通过上图可以看出，红色的三角形占比为2/3，蓝色正方形占比为1/3，因为红色三角形的占比大于蓝色正方形的占比，所以绿色的圆被赋予为红色三角形的类别。如果取k=5，通过上图可以看出，红色的三角形占比为2/5，蓝色正方形占比为3/5，因为红色三角形的占比小于蓝色正方形的占比，所以绿色的圆被赋予为蓝色正方形的类别。

在KNN算法中，你会发现影响KNN算法准确度的因素主要有两个：一是计算测试对象与训练集中各个对象间的距离；二是k的个数的选择。

2.算法流程：

  第一步，从网上获取的RSSI数据集中将RSSI数据分离并转化成数组类型方便使用数据。分为训练集和验证集两部分。

  第二步，将上一步分离出来的训练集数据放入矩阵中，设置参数k来控制矩阵大小并把k作为实验的唯一变量。

  第三步，将训练集的RSSI数据作为输入，通过计算数据集中各个测试点的欧式距离预测出目标点的大致距离。

  第四步，将预测点的坐标与验证集中的实际坐标进行比较，分析误差和影响因素。

3.数据集的选择：

由于本系统结合的是KNN算法，所以在系统实现中需要用到大量的准备好的数据。受到疫情影响和测量工具的不足，本人无法亲自使用实际测量工具来得出数据并用其作为本次实验的样本。但我前往PIN网站上找到了实现本次实验需要的RSSI数据集。

图中，offline_data_uniform.m存放的是用来测试KNN算法计算的数据集， offline_data_random.mt存放的是用来测试KNN预测精确度的数据集。

4.计算欧式距离：

 为了推测出预测点的大致范围，就要计算出其他点之间的欧式距离。然后对求得欧式距离排序，取前k个最小值，最后对这k个位置的坐标求平均即得到待定位点的估计位置，然后对应的找到所在的网格的坐标；

 5.结果处理：

  初步设置为取预测结果与实际结果误差距离小于5m的合格预测点记为分子，取所有的预测点数记为分母。两者相除，得到预测精度百分比。将k的值从加到30（即实验范围不断的扩大），观察对预测精度的影响。

三.详细设计

1.开发环境：系统：windows10 开发语言：python3.10 开发环境：pycharm

 2.具体代码：

(1)主程序：

from k_nearest_neighbor import KNearestNeighbor

import scipy.io as sio
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

 #将训练集和验证集这两个数据集提取出来上传到dataset里面
dataset = sio.loadmat('D:/data/offline_data_uniform.mat')
dataset1 = sio.loadmat('D:/data/offline_data_random.mat')
print(list(dataset1))

#由于数据集是字典类型的，我们只需要从里面取出蓝牙RSS数据和定位的坐标这两种元

素即可，并且把它们转化成为数组方便我们进行后续操作

rss_for_test = np.array(dataset['offline_rss'])
rss_for_train = np.array(dataset1['offline_rss'])
coordinate_for_test = np.array(dataset['offline_location'])
coordinate_for_train = np.array(dataset1['offline_location'])

#根据检查，两个数据集中的数据均有高达5万条，全用于计算会使得电脑设备过热超频并且计算效率缓慢，综合考虑，我们选用了2万条数据进行算法的训练和预测，用五千条实际数据进行验证实验的准确性。
rss_train = rss_for_train[:20000]
coordinate_train = coordinate_for_train[:20000]
rss_test = rss_for_test[:5000]
coordinate_test = coordinate_for_test[:5000]




if __name__ == '__main__':
    classifier= KNearestNeighbor()
    classifier.train(rss_train,coordinate_train)
    dists=classifier.compute_distances_no_loops(rss_test)#计算欧氏距离

    #选取多组k值，寻找准确率较高的k的取值
    for k in range(1,31):
        y_test_pred = classifier.predict_labels(dists, k)
        # 计算测试集中数据的预测坐标与真实坐标的欧式距离
        coordinate_dist = classifier.compute_coordinate_dist(coordinate_test,y_test_pred)
        #统计预测坐标与真实坐标误差小于500cm的样本数量
        num_correct = np.sum((coordinate_dist<150) == True)
        # print(num_correct)
        num_test = rss_test.shape[0]
        accuracy = float(num_correct) / num_test
        print ('k取%d，一共测试了%d个预测点,其中满足误差小于1.5m的有%d个点, 预测准确度: %f' % (k,num_test,num_correct, accuracy))

   

（2）KNN类（副）

import numpy as np
#设计一个KNN的类别，方便用与外部函数对其属性的调用并使自身的层次更清晰明了
class KNearestNeighbor(object):


  def __init__(self):
    pass
#加载数据
  def train(self, X, y):
    self.X_train = X
    self.y_train = y

#采用介绍的公式来计算欧式距离
  def compute_distances_no_loops(self, X):
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    test_sum = np.sum(np.square(X), axis=1)
    train_sum = np.sum(np.square(self.X_train), axis=1)
    inner_product = np.dot(X, self.X_train.T)
    dists = np.sqrt(-2 * inner_product + test_sum.reshape(-1, 1) + train_sum)
    return dists

#计算测试集中数据对应的预测坐标结果
  def predict_labels(self, dists, k=1):
    #根据距离矩阵中一个元素（元素表示的是测试点和训练点之间的距离）
    num_test = dists.shape[0]
    y_pred = np.zeros((num_test,2))
    for i in range(num_test):
      #对距离按列方向进行从小到大排序,输出对应的索引
      y_indicies = np.argsort(dists[i, :], axis=0)
      # 找到前k个最近的距离的坐标
      closest_y = self.y_train[y_indicies[: k]]
      #求出k个最邻近坐标的平均值
      y_pred[i] = np.mean(closest_y,axis= 0)
    return y_pred

#计算测试集中数据的预测坐标与真实坐标的欧式距离
  def compute_coordinate_dist(self,coordinate_test,y_pred):
    num_test = coordinate_test.shape[0]
    coordinate_dist = np.zeros((num_test,1))
    for i in range(num_test):
      coordinate_dist[i] = np.sqrt(np.sum(np.square(coordinate_test[i,:]-y_pred[i,:])))
    return coordinate_dist

四.测试数据及其结果分析

  1.运行结果：

如图所示，误差期望值设置为预测点与实际点的欧式距离小于5m，给出的总预测点个数为5000个，实际上满足误差允许条件的点大概有4650个左右，精度大概维持在93%左右。

一开始的k值较低时，预测精度仅有88%，这是由于k=1所代表的训练范围较小，各个点位之间的参数较单一，没有太多的相互参照物。但随着训练点数的范围不断扩大，精度在不断上升，最后稳定在93%左右波动。

上图所示，我将误差允许范围缩短到了1.5m，实验结果清晰可见，在5000个预测点中满足要求的仅有2500左右，精度在50%左右。分析如下：数据的来源问题，由于本次的数据样本来源于网络，不能确保数据测量的准确性，这对预测和计算是至关重要的一个因素。其次，KNN算法也存在着一定的局限性，预测结果容易受噪声数据的影响，当样本不平衡时，新样本的类别偏向训练样本中数量占优的类别，容易导致预测错误。

五、课程设计总结

总结内容包括：

（1）课程设计过程中的问题

1.数据集的内容未知且无法上传：

问题：由于数据集是在网上寻找的，是个mat文件，一开始并不清楚其中的元素和数据是什么成分，故不能直接引用该数据集。

解决方法：在PyCharm中用load函数先将文件在后台打开，再用print打印出数据集，得知其为字典型数据后在进行后续操作。

2.问题：数据量太大，程序揉碎在一起，太过于繁琐，层次混乱。

解决方法：建立了一个KNN的类，在类里面声明了计算欧式距离，预测点的位置，校验准确度这3个主要函数，并通过for递归语句，一层一层的解决k的值从1到30排列。显得程序条例明确，层次分明。

3.问题：一开始实验结果并不精确，误差为5m以内的点的预测精确度只有40%

解决方法：经过实验结果的比对，一开始我设置的训练点数仅有3000点，预测点能参考的对象较少，对于结果的影响较大。我们将训练点数扩大到20000时，就有足够的点数坐标作为算法的训练对象，极高地提高了算法的准确度，减少了误差的可能。

（2）课程设计过程的收获和感受。

通过这次数据结构的程序设计也让我懂得了怎么样去设计一个程序。从问题分析中找出程序所要解决的关键问题和数据结构算法的选择;在概要设计中完成程序的大体轮廓;在详细设计中解决关键问题的算法和设计;在调试分析中完成程序最终的修补；在数据处理中分析结果误差的原因。