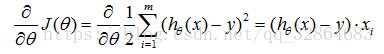线性回归原理及实现（二）：梯度下降法

        之前我写的一篇博客《线性回归原理及实现（一）：最小二乘法》写了有关线性回归的基本原理和应用场景的内容，提到了两个实现线性模型回归的方法：最小二乘法和梯度下降，并给出了最小二乘法的推导和python实现代码；这篇博客则是承接上一篇没有写完的内容，主要写线性回归的梯度下降法的原理和代码实现。

        其实梯度下降非常容易理解，如果将损失函数的分布简化理解成一张凹凸不平的曲面，那么梯度下降的过程就有点像我们郊游爬到山顶后下山的过程，如果我想要最快地到达山脚，那么我就要尽量地选择路面更陡的路线；梯度下降也相似，如果损失函数要尽快地找到一个最小值（暂且先不管是局部最小还是全局最小），那么参数就要沿着损失函数梯度的方向变化，每一步的变化都是沿着当前位置的梯度方向。循环迭代，如果当损失函数变化很小并趋近于收敛，那么我们可以把当前位置近似看作是一个最小值位置，最终得到的参数向量就是我们线性回归模型的最终参数。

        和上一篇博客《线性回归原理及实现（一）：最小二乘法》中的损失函数的定义一样，梯度下降的迭代终止条件也是让损失函数的值趋于最小，损失函数的定义如下：

对损失函数求每一个参数分量的偏导数，用整个参数向量θ表示为：

更新过程可以理解成：θi沿着梯度下降最快的方向进行递减的过程。左边的θi表示更新之前的值，等式右边表示沿着梯度方向减少的量，α表示步长，也称作学习速度，这个值需要人工手动设置。

其实在实际程序运行的过程中，算法本身对α取值的大小是非常敏感的！如果α太小，可能导致学习速率太小，收敛速度非常慢；如果α取值太大，可能导致直接在迭代的过程中直接错过了最小值，导致无法收敛。

不断更新θi的值直到J(θ)收敛，可以通过比较J(θ)的前后两个值是否有发生变化（继续下降），当没有发生变化时表示已经达到了最小值（可能是局部最小值）。

其实这种梯度下降的方法就是一种最简单的梯度下降法，我们叫它批量梯度下降，总结一下，它算法流程很简单：

        这种方法的缺点就是得到的最小值有可能是局部最小，为了解决这个问题有很多改进的梯度下降算法，比如最典型的随机梯度下降（SGD），随机梯度下降通过每个样本来迭代更新一次参数，可能未遍历整个样本就已经找到最优解，大大提高了算法的收敛速度。 最小化每个样本的损失函数，虽然每次迭代结果不一定都是全局最优解，却总是沿着这个方向发展，故最终结果总是接近全局最优解。虽然SGD应用远比批量梯度下降要广泛，但这里就暂不讨论SGD算法，接下来就是python代码实现。

该程序中使用的数据集是sklearn库中有关房价的数据集，最终的迭代终止条件为损失函数的每一步的变化要小于0.1，程序中步长为0.00000001，根据测试，若再增加一个数量级0.0000001则导致不能收敛。

代码如下：

#coding=utf-8
import numpy as np
import math
from sklearn.datasets import load_boston#导入数据集的包
from compiler.ast import flatten

#使用梯度下降法的线性回归
class LinearRegression2:
    def __init__(self,data,target):#data、target分别为点的坐标向量和对应的实际映射值
        self.data=data
        self.target=target
        self.theta=flatten((np.zeros((1,len(data[0])))).tolist()) #参数都初始化为0
        for i in self.theta:
            i=i+1
        self.last_loss=self.loss_fun()+1#last_loss保存最近一次梯度下降之前的损失函数
    def hypothesis(self,X):#估计函数、其中所有的参数用theta表示
        result=0
        for i,j in zip(X,self.theta):
            result=result+i*j
        return result
    def loss_fun(self):#损失函数
        loss=0
        for i,j in zip(data,target):
            loss=loss+0.5*(self.hypothesis(i)-j)**2
        return loss
    def update_theta(self,step_length=0.01):#参数更新参数、step_length表示梯度下降的步长
        self.last_loss=self.loss_fun()
        new_theta=[]
        for j in range(len(self.theta)):#对每个参数theta都计算梯度
            gradient=0#表示梯度
            for i in range(len(self.data)):
                gradient=gradient+(target[i]-self.hypothesis(data[i]))*data[i][j]#计算梯度
            # print gradient
            new_t=self.theta[j]+step_length*gradient#批量梯度下降
            new_theta.append(new_t)
        self.theta=new_theta#更新参数向量theta
    def regress(self):
        step_count=0
        while True:
            step_count=step_count+1
            self.update_theta(0.00000001)
            print self.theta,'\n',self.loss_fun()
            if math.fabs(self.loss_fun()-self.last_loss)<0.1:
                break
        print "After ",step_count,"steps,achieve iterative convergence!"
    def predict(self,X):
        result=0
        for i,j in zip(X,self.theta):
            result=result+i*j
        return result

if __name__ == '__main__':
    #从sklearn的数据集中获取相关向量数据集data和房价数据集target
    data,target=load_boston(return_X_y=True)
    LR=LinearRegression2(data,target)
    LR.regress()#线性回归模型的训练，梯度下降可能需要一段时间，如果先时间太长可以把参数保存到文件中，之后每次运行程序可以直接预测
    #选取一部分的样本用来验证最终回归模型的效果
    test_data=[]
    for i in range(len(data)):
        if i%17==0:
            test_data.append([data[i],target[i]])
    for i in test_data:
        print "real: ",i[1],"  estimate: ",LR.predict(i[0])

结果演示：

After  14665 steps,achieve iterative convergence!
real:  24.0   estimate:  28.820134550334217
real:  17.5   estimate:  22.563782047531213
real:  13.5   estimate:  15.215626994274198
real:  20.5   estimate:  25.728238663633107
real:  17.4   estimate:  20.019124305046283
real:  26.6   estimate:  25.166168073735196
real:  18.6   estimate:  14.60919799310189
real:  19.3   estimate:  20.954353251018468
real:  17.4   estimate:  21.361348239779748
real:  19.4   estimate:  16.378810375619906
real:  17.4   estimate:  18.19111662421971
real:  32.0   estimate:  28.339788430160112
real:  50.0   estimate:  35.33171777252018
real:  21.7   estimate:  18.67465558212994
real:  23.7   estimate:  23.677540463875367
real:  20.9   estimate:  27.76087993237549
real:  24.4   estimate:  26.67994246330653
real:  24.8   estimate:  24.30275706896671
real:  33.4   estimate:  31.484475792420337
real:  18.5   estimate:  23.50499361187146
real:  18.7   estimate:  23.877000243174763
real:  21.7   estimate:  25.703591230767476
real:  13.8   estimate:  7.166655360758007
real:  23.2   estimate:  20.105108701909337
real:  17.2   estimate:  13.782710457064088
real:  8.3   estimate:  2.8082486610399364
real:  18.4   estimate:  24.271606984223574
real:  20.0   estimate:  23.68620444198985
real:  16.7   estimate:  22.316143922363352
real:  21.8   estimate:  21.23638166742458

        可以看到，经过14665次迭代，达到终止要求。上面的列表是从原数据集中抽取序号为17的倍数的数据项作为测试数据，real后面的值为原真实值，estimate后面的值为预测值。通过观察可以发现，预测值和真实值之间的差距还是存在的，毕竟是线性模型，不能非常精确地去拟合，但是预测值的大小对于真实值还是有参考意义的。