关于空间域卷积和频率域卷积
前段时间看了很多的概念和知识,发现因为是走马观花的过了一遍,所以看得稀里糊涂的,然后许多地方混淆了概念,特别是关于图像频率域的部分的理解(包括图像频率域滤波之类的),所以下面总结一下这段时间重新看《数字图像处理》(电子工业出版社,Matlab本科教学版)第三章重新收获的关于频率域的理解。
首先,我们要明确的概念是空间域和频率域,我们通过imread函数得到的一幅图像(基本上也是我们平时说的图像),是处在空间域的,也就是说用f(x,y)表征的某一点的灰度值(或者是单色图像中某一点的亮度)的这种形式,就是在空间域里面。
那么什么是图像的频率域呢?理解了图像的频率的概念,就不难理解频率域。我个人理解是这么类比的,图像可以看成是一个特殊的二维的信号,然后某一点的灰度级,其实就是图像信号上这一点的”幅度“,那么根据信号的概念,频率就是信号变化的快慢,这样就好理解了,所谓的频率也就是这个图空间上的灰度变换的快慢,或者是叫图像的梯度变化,什么地方梯度频率比较大呢?这在图像中自然是“边界”比较大。举个例子来讲,如果一幅图整体变化不大(比如说是一面墙的图),那么他在频率域下低频成分就很多,而高频成分就极少。而显然如果是一幅国际象棋棋盘,他的高频成分相对刚才那幅墙的图片来说,肯定多得多。
然后从图像域变换到频率域,我们用的函数就是大名鼎鼎的二维离散傅里叶变换了:
令f(x,y)表示一幅大小为MXN像素的数字图像,其中,x=0,1,2······M-1, y=0,1,2······N-1,由F(u,v)表示的f(x,y)的二维离散傅里叶变换(DFT)由下式给出:
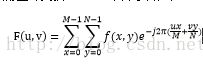
式子当中,u也是属于0到M-1,v属于0到N-1。频率域就是属于u,v作为频率变量,由F(u,v)构成的坐标系,这块MXN的区域我们通常称为频率矩形,很明显频率矩形的大小和输入图像的大小相同。
有傅里叶变换,当然就有傅里叶反变换(IDFT):
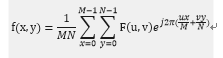
这里多提一句,按照书上的说法,在DFT的表达式中,1/MN项出现在正变换前面,而在有些表达式中就如上式那样出现在反变换前面,因为Matlab采用的是后者,所以书上的公式就是用的上式那种了。
由上面的公式可以看出几个点:
-
不难看出,F(0,0)等于f(x,y)平均值的MN倍,因为带入到傅里叶变换公式中可以得到F(0,0)实际上就是图像中所有f(x,y)求和。所以我们也常把F(0,0)称作傅里叶变换的直流分量。
-
我们可以很明显的看出,在频率域中的一点(u,v)的值F(u,v),他并不决定于空间域中(x,y)的值,而是跟整个图像空间域中的所有的点都有关系,因此,在频率域中的一点(u,v)的值,例如说F(5,5)和空间域上的这一点f(5,5)并没有什么关系,而是决定于整幅图像。
接下来书上讲了傅里叶变换的一些性质,还有傅里叶谱,变换的相角定义,功率谱定义等等概念,因为打公式太麻烦,这里就不多赘述了,可以在网上找到现成的公式定义和概念。
傅里叶变换性质里面个人认为比较重要的是周期性,因为周期性的缘故,所以在傅里叶变换过后的频率图里,四角的是低频分量(具体的我也不太清楚,但是比如低频分量),我们到时候会把低频分量移到中心位置来,因为大部分图像的低频分量其实更多,所以会在边角上比较亮,放到中间来比较好看。
下面举例一幅图说明看一幅频率域傅里叶谱图:
f=imread(‘3.jpg’);
imshow(f);%显示原图
F=fft2(f);%做傅里叶变换
S=abs(F);%取傅里叶谱
figure,imshow(S,[]);%显示傅里叶谱

左图是原图,右图是频率图,频率图中的亮暗说明了对应频率的多少,上面已经谈过,如果从右图可以看出来是边上的四个点比较亮,这说明原图中低频分量比较多,也就是说原图中的变化比较少。换句话来说,如果原图看成地形的话,那说明大部分地形非常平坦。
我们可以通过公式(欧拉公式e^(2pij)=1以及指数的计算),可以很容易发现(图是盗的- -):

上式最左边那个符号表示求傅里叶变换。由上式知道这么弄一番之后,是可以把频率图的原点放到中心的。
在matlab中用的是fftshift函数。
居中过后的频率谱显示如下:

可以看得更清楚一些,这个时候因为其实频率谱的范围是很大的,相对于低频分量来说,高频分量的值比较少,所以可以用对数变换(log(1+abs(F))将高频细节扩展出来,显示如下:

下面谈谈对滤波的理解,不知道是不是完全正确。
滤波和算子都是数字图像处理的基本操作,其中滤波是指在像素领域(空间域)内做领域处理(中值滤波、均值滤波)或者在图像频域内(需要先做傅里叶变换)做处理(低通滤波、高通滤波、带通滤波)。算子一般就是指的是卷积算子了。
先来谈谈空间域的滤波。什么叫领域处理呢?领域处理的就是对领域进行一系列的操作:
(1) 选取中心点(x,y);
(2) 仅对预先定义的点(x,y)的领域内的像素执行操作;
(3) 令运算结果为该点处的响应;
(4) 对图像中的每一点重复该处理。
中心点移动的过程中会产生新的领域,每个领域对应输入图像上的一个像素。用来标识该处理的两个主要术语是领域处理和空间滤波,其中后者更为通用。如果对领域中像素执行的计算是线性的,则称该操作是线性空间滤波。(也用术语空间卷积);否则称为非线性空间滤波。
线性操作包括领域中的每个像素乘以相应的系数,将结果求和,从而得到点(x,y)处的响应。若领域的大小为mxn,则需要mn个系数。这些系数被排列为一个矩阵,称为滤波器(模板)/滤波模板/核/掩模或者窗口。其中前三个属于最常见。为变得更明显一些,也用卷积滤波、卷积模板或者卷积核等术语。
再来说下卷积算子是个什么意思:
在这里盗一下网上的图:

然后如上所示,图片中右上角的那个矩阵h=[2 9 4;
7 5 3;
6 1 8;]
就是后面经常提到的模板了,在相关书本上一般也写作w(x,y)。如果把基于乘积和的值用来替代成原来的(x,y)的值,那么这种滤波方式叫做线性滤波(比如拉普拉斯算子)。其他的叫做非线性滤波。
空间域滤波的最常见的就是中值滤波和均值滤波,顾名思义,中值滤波就是用图像领域中所包含的像素的排序集合的中值进行替代,而均值滤波是用领域像素们的均值进行滤波。中值滤波也属于统计排序滤波。
接下来介绍频率域的滤波:
首先,有个定理,叫做卷积定理:
f(x,y)★h(x,y)óH(u,v)F(u,v)
上式中★代表卷积,ó代表一个傅里叶变换对。
频率域的滤波比较多的就是高斯低通/高斯高通滤波器了,和空间域稍微有区别的是,在频率域内不是进行的领域处理,而是进行的是函数修改:
G(u,v)= H(u,v)F(u,v)
函数H(u,v)又叫做滤波器传递函数,频率域滤波的思想就是选择一个滤波器传递函数,该函数按照指定的方式修改F(u,v)。
由卷积定理可知,在频率域中让F(u,v)乘以空间滤波器的傅里叶变换H(u,v),再做一个傅里叶反变换,就可以得到用空间域滤波器滤波后的图像了(这也是相当于用DFT的方式在做卷积,用这种方式做卷积又叫循环卷积)。
值得一提的是,注意,当作循环卷积的时候,因为F和H都是周期函数,所以G必然也是周期函数,在周期接近函数非零部分的持续周期时对周期函数进行卷积会引起相邻周期的串扰(这种串扰又叫折叠误差),所以要通过补零的方法来避免。比较拗口,还是举例来说明:一个上黑下白的方块图片,在DFT卷积的时候我们假设在处理上边沿了,结果因为是周期的所以上边沿其实在处理时会受到上边沿上面另一个方块的下边沿的白色部分的影响(具体的例子见书P63页),补0之后就不会受影响了。