python实现层次分析法(AHP)
相关文章:
python实现对应分析(CA)
python实现主成分分析(PCA)
python实现概率密度匹配法
1 层次分析法简介
层次分析法(Analytic Hierarchy Process,AHP)这是一种定性和定量相结合的、系统的、层次化的分析方法。
层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同的层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
2 层次分析法步骤
步骤如下图所示:
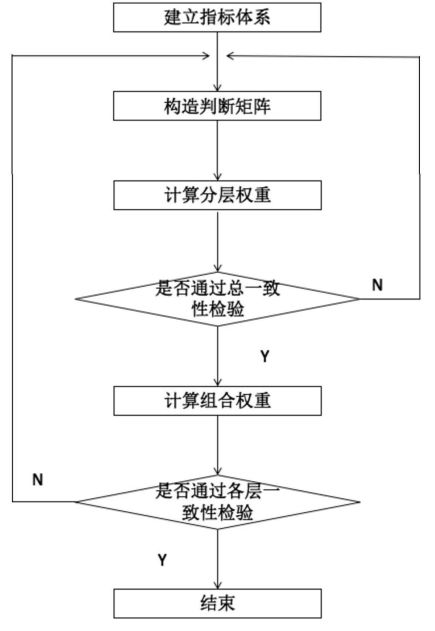
1)建立层次结构模型
将复杂问题层次化:
- 首先是目标层,即问题的最终目的;
- 将影响问题决策的因素分为几大类作为标准层;
- 最后一层是方案层,即列出各种方案。
把问题按照各因素之间的隶属关系或相互关联度分层,形成自上而下的逐层支配关系,即递阶层次结构,如下图所示:

2)构建判断矩阵
采用1-9标度法形成判断矩阵,方法是两两比较。
成对比较矩阵是表示本层所有因素针对上一层某一个*因素(准侧或目标)*的相对重要性的比较。成对比较矩阵的元素 a i j a_{ij} aij 表示的是第 i 个因素相对于第 j 个因素的比较结果,这个值使用的是Santy的1-9标度方法给出。

比如,上面的旅游的例子,在旅游问题中第二层A的各个因素对目标层Z的影响两两比较的结果如下图:

比如 a 14 = 3 a_{14}=3 a14=3 则表示的是景色因素比居住因素对于选择旅游地来说稍微重要。
3)计算分层权重及其一致性检验
a. 计算分层权重(层次单排序)
层次单排序:就是把一个层次上的因素相对上一层某个因素的重要性权重并归一化。该权值对应判断矩阵的最大特征值的特征向量的归一化值。
比如,方案层B1/B2/B3对A1\A2\A3\A4\A5的成对比较阵:

- B1/B2/B3对A1的权重为:[0.595, 0.276, 0.128]
- B1/B2/B3对A2的权重为:[0.082, 0.236 , 0.682]
- B1/B2/B3对A3的权重为:[0.429, 0.429, 0.143]
- B1/B2/B3对A4的权重为:[0.634, 0.192, 0.174]
- B1/B2/B3对A5的权重为:[0.167, 0.167, 0.667]
- A的权重:[0.264, 0.476, 0.054 , 0.099, 0.109]
b. 一致性检验
满足下面关系式的正互反矩阵可以叫做一致矩阵:
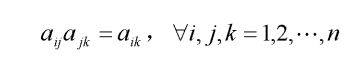
一致矩阵具有以下属性:
- 为正互反矩阵
- 转置也是一致阵;
- 各行成比例,则矩阵转秩为1;
- 最大特征根(值)为 λ=n ,其余的 n−1 个特征根均等于0;
- 任一列(行)都是对应于特征根 n 的特征向量, AW=nW ;
判断矩阵的最大特征值λ=n时为一致矩阵,且当判断矩阵非一致时,必有最大特征值λ>n,其中λ比n大的越多,判断矩阵非一致性越严重,则其对应的标准化特征向量就越不能反映出因素的影响。因此需要对矩阵进行一致性检验,步骤如下:
- 计算一致性指标 C I = λ m a x − n n − 1 CI=\frac{\lambda_{max}-n}{n-1} CI=n−1λmax−n。CI等于0时,有完全的一致性;接近0,有满意的一致性;越大,不一致性越严重。
- 查找CI对应的平均随机一致性指标RI:

RI的取值,不刻意的从[1-9]和[1-1/9]中,随便选择数字组成正互反矩阵,以此形式直到得到500个随机样本矩阵,然后计算出最大特征根的均值,并定义RI=(均值-n)/(n-1)。
- 计算一致性比例: C R = C I R I CR=\frac{CI}{RI} CR=RICI
- 当CR<0.1时,矩阵一致性可以接受。
4)层次总排序及其一致性检验
计算某一层次所有因素对于 最高层(总目标) 相对重要性的权值,称为层次总排序。

层次结构总排序也需要一致性测试,从上层到下层逐层进行。设 A A A层的权值向量为 a 1 , a 2 , . . . a_1,a_2,... a1,a2,...,B层对 A 1 A_1 A1的判断矩阵的 C I CI CI和 R I RI RI为 C I 1 , R I 1 CI_1,RI_1 CI1,RI1,B层对 A 2 A_2 A2的判断矩阵的 C I CI CI和 R I RI RI为 C I 2 , R I 2 , . . . CI_2,RI_2,... CI2,RI2,...,则:
C R = a 1 C I 1 + a 2 C I 2 + . . . a 1 R I 1 + a 2 R I 2 + . . . CR=\frac{a1CI1+a2CI2+...}{a1RI1+a2RI2+...} CR=a1RI1+a2RI2+...a1CI1+a2CI2+...
至此,根据最下层(决策层)的层次总排序做出最后决策。
3 层次分析法优缺点
优点:
- 充分考虑定性因素的影响作用,加强选择依据的可靠性,减少判断失误。
- 传统方法模型复杂,AHP采用1-9标度法形成判断矩阵,简单易懂。
- 将专家经验和判断融入递阶层次结构中,对问题综合评判,弥补传统方法片面注重量化信息,缺乏柔性的不足。
缺点:
- 当因素较多,判断矩阵不易达到一致性,且调整困难。
- 不能较好地处理不确定性因素。
- 各专家对于指标之间的重要度评判不同,易存在个人主观片面性。
4 Python实现
# 参考:https://blog.csdn.net/lwq_0/article/details/107296446
def Eigenvalues_Feature_vector(phalanx):
# 计算判断矩阵的特征值和特征向量
a, b = np.linalg.eig(phalanx)
# print("特征值是\n", a)
print("特征值实部:", a.real) # 显示特征值实部
max_eigenvalue = max(a.real)
print("最大特征值:", max_eigenvalue)
num_shape = phalanx.shape
CI = (max_eigenvalue - num_shape[0]) / (num_shape[0] - 1)
print("---->> CI=", CI)
if num_shape[0] == 2:
RI = 0
elif num_shape[0] == 3:
RI = 0.52
else:
RI = 0.89
if RI == 0 and CI == 0:
CR = 0
print("---->> CR=", CR)
else:
CR = CI / RI
print("---->> CR=", CR)
if CR < 0.1:
print("---->> 一致性比例可接受!")
else:
print("---->> 一致性检验不通过!")
print("\n")
# print("特征向量是\n", b) # numpy的特征向量是竖方向的,numpy输出的特征向量是单位化后的向量
print("特征向量实部:", b.real)
return b
def Weight_vector(phalanx):
# 计算判断矩阵的权向量
num = 0
b = Eigenvalues_Feature_vector(phalanx)
for i in range(len(b.real)):
num += b.real[i][0]
print("\n")
print("指标权重是:")
weight_list = []
for j in range(len(b.real)):
weight_num = b.real[j][0] / num
weight_list.append(weight_num)
print(weight_list)
print("\n")
return np.array([weight_list])
参考:
https://zhuanlan.zhihu.com/p/38207837
https://blog.csdn.net/lwq_0/article/details/107296446
基于层次分析法的研学旅行综合评价指标体系研究-金淼.