机器学习中的数学：概率图与随机过程

概率图模型导论

1. 概率图的最基本含义

概率图，从字面上理解就是“概率”+“图”，“概率”指的就是概率模型，在前面的博客里，我们介绍了一些非常基础的概率模型，我们发现把概率引入到机器学习的世界里是一件非常自然的事情，这样我们就能够实现对已有的数据进行聚类（例如混合高斯模型），或者对未知的数据进行预判（例如朴素贝叶斯、逻辑回归等），这是机器学习的核心思想。

“图”和我们在数据结构中学习过的图是一个意思，它包含了有向图、无向图。

对上述的图结构赋予概率的内涵，即将概率嵌入到图结构当中，形成概率图模型。这么干，一方面会使得表达上更为清晰直观，另一方面可以用图结构把概率的特征体现的更加明显，以便于我们去构造一些更加高级的模型。

2. 经常处理的概率和运算法则

用来描述样本的数据往往是多维的，因此在现实中一般都是用高维、多元的随机变量来表示数据。例如一个 p维的随机变量 (x1,x2,x3,…,xp)，我们一般会关注几种概率分布的形式：

联合概率：p(x1,x2,x3,...,xp)

边缘概率：p(xi)
条件概率：p(xi|xj)

很多问题的研究，其实实际上都是围绕着这三个概率展开的。

此时我们再回顾一下围绕着这三个概率的运算符法则，其实无非都是条件概率、联合概率、边缘概率之间的转换规则如下。

和准则：

p(x1)=∫p(x1,x2)dx2

积准则：

p(x1,x2)=p(x1)p(x2|x1)=p(x2)p(x1|x2)

链式法则：

p(x1,x2,…,xp)=p(x1)p(x2|x1)p(x3|x2,x1)…p(xp|xp−1xp−2…x1)

贝叶斯法则：

p(x2|x1)=p(x1,x2)p(x1)=p(x1,x2)∫p(x1,x2)dx2=p(x2)p(x1|x2)∫p(x2)p(x1|x2)dx2

3. 高维随机变量的困境与解决探索

随机变量的维度高了，自然而然的就使得联合概率 p(x1,x2,x3,…,xp)的计算非常复杂，看看那个链式法则吧，看着它似乎还是非常复杂，一脸懵。

那么面对复杂，人们自然而然的就想着去简化模型，简化的方法，就是施加某些前提假设，来化解这其中的复杂性。

首先要提的就是朴素贝叶斯模型，在描述以类别为条件的概率 p(x1,x2,x3,…,xp|y)
中，它假设给定类别 y的情况下，高维随机变量中各个维度是彼此独立的，在这个前提下，概率就非常容易的得到了分解：

p(x|y)=p(x1,x2,x3,…,xp|y)=p∏i=1p(xi|y)

朴素贝叶斯简便归简便，但是问题在于它的假设过强了，实际中，高维随机变量的各个维度之间有极大的可能性是互相不独立的，因此这个 xi⊥xj|y

前提假设就不存在，也就不能按照这个方式进行分解了。

我们进一步的放松这个前提假设，就不得不提在随机过程中介绍过的齐次马尔科夫模型（我们以一阶为例）：

图1 马尔科夫链

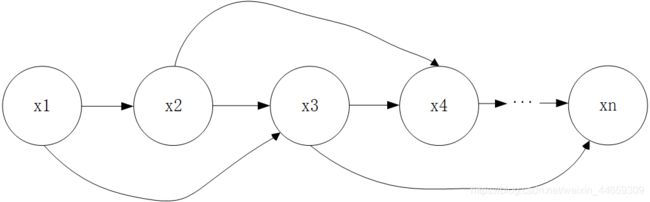
在这个我们熟悉的一阶马尔科夫模型中，我们知道，x3的状态仅与 x2 相关，而与 x1 无关，x4 的状态仅与 x3 有关，而与之前的 x1、x2 均无关，即用表达式 xj⊥xi+1|xi,j

来表示，通过这种方式也达到了简化联合概率表示形式的目的：

p(x1,x2,x3,x4,…,xp)
=p(x1)p(x2|x1)p(x3|x2,x1)…p(xp|xp−1xp−2xp−3…x1)=p(x1)p(x2|x1)p(x3|x2)…p(xp|xp−1)

联合概率的表达形式也得到了简化，但是话说回来，一阶马尔科夫性的假设实际上也过强了，因为它把各个维度之间的依赖和关联关系限定的过于简单和单一，实际上许多的依赖关系绝不仅仅限于此，比如下面这种：

图2 较为复杂的依赖关联关系

我们随意在几个维度之间增加了依赖关联关系，马尔科夫性就无法描述这种情形了。

因此我们还需要进一步的去探索更为泛化的方法来化解高维随机变量的复杂性，这是概率图模型的一个非常核心并且非常首要的问题，有了合适的方法，我们就能一方面利用概率图来直观地表示高维随机变量，另一方面又能够很好地化解它的复杂性。这一块的内容我们放在下一讲单独讲解。
4. 概率图中的几个主要研究目标

好了到了这里，我们引出了概率图模型的概率和由来，讲了它的一个基本问题，我们暂时停一停。先从整体上来概览一下概率图模型的全貌，以及我们需要重点去研究哪些问题：

概率图模型中有三大基本问题：表示（representation）、推断（inference）和学习（learning）。

数据结构中，图分为有向图和无向图，那么概率图同样也就分为了有向图和无向图，其中有向图称为是贝叶斯网络，而无向图称为是马尔科夫网络（或者称之为马尔科夫随机场），这就是概率图的表示，我们在这一章中，先介绍有向图模型，然后再介绍无向图模型。

推断问题的本质就是根据已知的数据，去求另外一些数据的概率分布，有精确推断，以及在工程中使用更广的近似推断。

学习问题就更好理解了，主要是学两块内容，一块是参数学习，另一块是结构学习。