论文笔记--知识表示学习研究进展-2016
论文信息:
论文-知识表示学习研究进展-2016-刘知远
文末附6篇知识表示相关论文的下载地址
文章目录
- 前言
-
- 知识库的主要研究目标
- 基于网络形式的知识表示面临的困难点
- 表示学习&知识表示学习
- 本文目标
- 知识表示学习介绍
-
- 表示学习的概念和理论
- 知识表示的应用和优点
- 知识表示学习的主要方法
-
- 距离模型
- 单层神经网络模型
- 能量模型
- 双线性模型
- 张量神经网络模型
- 矩阵分解模型
- 翻译模型
- 知识表示学习的挑战和解决
-
- 复杂关系建模
- 多源信息融合
- DKRL(考虑实体描述的知识表示学习)模型
- 关系路径建模
- 资源下载
- 参考文献
前言
知识库的主要研究目标
从无结构或半结构的互联网信息中获取有结构知识,自动融合构建知识库、服务知识推理等相关应用,自动融合构建知识库、服务知识推理等相关应用。知识表示是知识获取与应用的基础,因此,知识表示学习问题是贯穿知识库的构建与应用全过程的关键问题。
基于网络形式的知识表示面临的困难点
- 计算效率问题;
- 数据稀疏问题:大规模知识库遵循长尾分布;
表示学习&知识表示学习
- 表示学习旨在将研究对象的语义信息表示为稠密低维实值向量
- 知识表示学习则面向知识库中的实体和关系进行表示学习。…
本文目标
介绍知识表示学习的最新进展,总结该技术面临的主要挑战和可能解决,并展望该技术的未来发展方向(见原论文[1])。
知识表示学习介绍
表示学习的概念和理论
概念
表示学习通过机器学习将研究对象的语义信息表示为稠密低维实值向量。
在该低维向量空间中,2个对象距离越近则说明其语义相似度越高。通常将研究对象表示为向量:实体 e 表示为le;关系 r 表示为 lr;通过欧氏距离或余弦距离等方式计算任意2个对象之间的语义相似度。
独热表示(one-hot representation)
独热表示是信息检索和搜索引擎中广泛使用的词袋模型的基础。
举例来说。一个网页中有W个不同的词,则在词袋模型中都被表示为一个W维的独热表示向量。在此基础上,词袋模型将每个文档表示为一个W维向量,每一位表示对应的额词在该文档的重要性。将研究对象表示为向量,该向量只有某一维非零,其他维度上的值均为0.有多少个不同的研究对象,独热表示向量就有多长。
优点:无学习过程,简单高效
缺点:假设所有对象都是相互独立的,无法利用语义相似度信息。导致无法有效表示短文本、容易受到数据稀疏问题影响的根本原因。
分布式表示(distributed representation)
表示学习得到的低维向量表示是一种分布式表示,是受到人脑工作机制启发。
现实世界中的实体是离散的,人脑通过大量神经元上的激活和抑制存储这些对象,而每个单独神经元的激活或抑制并没有明确含义,但是多个神经元的状态则能表示世间万物。
分布式表示的向量可以看作模拟人脑的多个神经元,每维对应一个神经元,而向量中的值对应神经元的激活或抑制状态。
此外,现实世界存在层次结构,这种层次或嵌套的结构反映在人脑中,形成了神经网络的层次结构。
知识表示的应用和优点
应用
- 相似度计算。利用实体间的分布式表示,可以快速计算实体间的语义相似度。
- 知识图谱补全。构建大规模知识图谱,需要不断补充实体间的关系,利用知识表示模型,可以预测2个实体的关系,这一般称为知识库的链接预测(link prediction),又称为知识图谱补全(knowledge graph completion).
- 其他。如关系抽取、自动问答等。
优点
- 提升计算效率。
- 缓解数据稀疏。表示学习将对象投影到统一的低维空中,使每个对象均对应一个稠密向量,从而有效缓解数据稀疏问题。
- 实现异质信息融合。不同来源的异质信息需要融合为整体才能得到有效应用。大量实体和关系在不同知识库中的名称不同,如何实现多知识库的有机融合,对知识库的应用有重要意义。通过设计合理的表示模型,将不同来源的对象投影到同一个语义空间中,就能建立统一的表示空间,实现多知识库的信息融合。
知识表示学习的主要方法
定义几种符号
将知识库表示为 G = ( E , R , S ) G=(E,R,S) G=(E,R,S), 其中 E = e 1 , e 2 , … , e ∣ E ∣ E=e_1,e_2,…,e_{|E|} E=e1,e2,…,e∣E∣是知识库中的实体集合; R = r 1 , r 2 , … , r ∣ R ∣ R=r_1,r_2,…,r_{|R|} R=r1,r2,…,r∣R∣ 是知识库中的关系集合;而 S ⊆ E × R × E S⊆E×R×E S⊆E×R×E代表知识库中的三元组集合,一般表示为 ( h , r , t ) (h,r,t) (h,r,t).
距离模型
结构表示(SE)中,每个实体用 d d d维的向量表示,所有实体被投影到同一个 d d d维空间中。
SE为每个关系 r r r定义了2个矩阵 M r , 1 , M r , 2 ∈ R d × d \boldsymbol M_{r,1},\boldsymbol M_{r,2}∈R^{d×d} Mr,1,Mr,2∈Rd×d, 用于三元组中头实体 ( h ) (h) (h)和尾实体 ( t ) (t) (t)的投影操作。
SE为每个三元组 ( h , r , t ) (h,r,t) (h,r,t)定义如下损失函数:
f r ( h , t ) = ∣ M r , 1 l h − M r , 2 l t ∣ L 1 f_r (h,t)=|\boldsymbol M_{r,1} l_h-\boldsymbol M_{r,2} l_t |_{L_1 } fr(h,t)=∣Mr,1lh−Mr,2lt∣L1
SE将头实体向量 l h \boldsymbol l_h lh和尾实体向量 l t \boldsymbol l_t lt通过关系 r r r的2个矩阵投影到 r r r的对应空间中,然后在该空间中计算两投影向量的距离。这个距离反映了2个实体在关系 r r r下的语义相似度。距离越小说明2个实体是这种关系的可能性越大。
实体向量和关系矩阵是SE模型的参数,SE将三元组作为学习样例,优化模型参数使损失函数不断降低。即通过计算
arg min r ∣ M r , 1 l h − M r , 2 l t ∣ L 1 \arg \min_r |\boldsymbol M_{r,1} l_h-\boldsymbol M_{r,2} l_t |_{L_1 } argrmin∣Mr,1lh−Mr,2lt∣L1
找到让两实体距离最近的关系矩阵,即它们之间的关系。
SE的缺陷是:它对头尾实体使用不同的矩阵进行投影,协同性较差,往往无法精确刻画两实体与关系之间的语义联系。
单层神经网络模型
SLM可以减轻SE无法协同刻画实体与关系的语义联系问题。缺点是其非线性操作仅提供实体和关系之间比较微弱的联系,但却引入更高的计算复杂度。
能量模型
语义匹配能量模型(SME)较为复杂。其定义多个投影矩阵和2种评分函数。
双线性模型
隐变量模型(latent factor model, LFM)提出利用基于关系的双线性变换,刻画实体和关系之间的二阶联系。LFM为每个三元组 ( h , r , t ) (h,r,t) (h,r,t)定义了如下双线性评分函数:
f r ( h , t ) = l h T M r l t f_r (h,t)=\boldsymbol l_h^T \boldsymbol M_r \boldsymbol l_t fr(h,t)=lhTMrlt
LFM取得巨大突破:通过简单有效防范刻画了实体和关系的语义联系,协同性较好,计算复杂度较低. 后来DISTMULT模型简化了LFM:
将关系矩阵 M r \boldsymbol M_r Mr设置为对角矩阵,实验表明这种简化极大降低模型复杂度,模型效果得到显著提升。
张量神经网络模型
张量神经网络模型(neural tensor network, NTN)基本思想是,用双线性张量取代传统神经网络中的线性变换层,在不同维度下将头、尾实体向量联系起来。如图4.1所示。
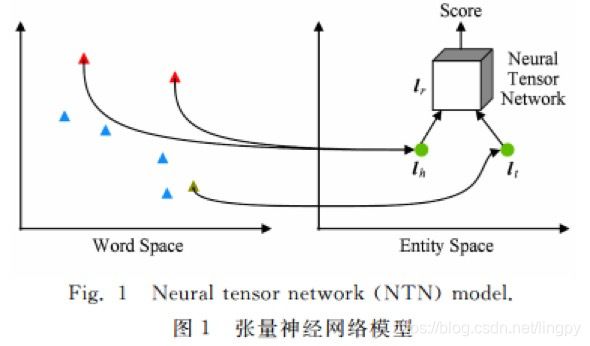
与以往模型不同的是,NTN中的实体向量是该是该实体中所有单词向量的平均值,这样做的好处是,实体中的单词数量远小于实体数量,可以充分重复利用单词向量构建实体表示,降低实体表示学习的稀疏性问题,增强不同实体的语义联系。
缺点是:计算复杂度较高;实验表明,在大规模稀疏知识图谱上的效果较差。
矩阵分解模型
代表方法是RESACL模型,其基本思想与LFM类似,不同之处在于,RESACL会优化张量中所有位置,包括0的位置;而LFM只会优化知识库中存在的三元组。
翻译模型
受到Mikolov等人2013年提出的word2vec模型中蕴含的词向量空间中平移不变现象(如 C ( k i n g ) − C ( q u e e n ) ≈ C ( m a n ) − C ( w o m a n ) C(king)-C(queen)\approx C(man)-C(woman) C(king)−C(queen)≈C(man)−C(woman))的启发,Bordes等人提出TransE模型,将知识库中的关系看作实体间的某种平移。
对于每个三元组,TransE用关系 r r r的向量 l r \boldsymbol l_r lr作为头实体向量 l h \boldsymbol l_h lh和尾实体 l t \boldsymbol l_t lt之间的平移。亦可以将 l r \boldsymbol l_r lr看作从 l h \boldsymbol l_h lh到 l t \boldsymbol l_t lt的翻译,所以TransE也称翻译模型。
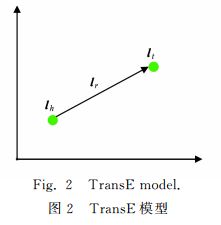
如图4.2,对于每个三元组,TransE希望:
l h + l r ≈ l t . \boldsymbol l_h+\boldsymbol l_r≈\boldsymbol l_t. lh+lr≈lt.
TransE模型定义了如下损失函数:
f r ( h , t ) = ∣ l h + l r − l t ∣ L 1 / L 2 , f_r (h,t)=|\boldsymbol l_h+\boldsymbol l_r-\boldsymbol l_t |_{L_1 /L_2 }, fr(h,t)=∣lh+lr−lt∣L1/L2,
即向量 l h + l r \boldsymbol l_h+\boldsymbol l_r lh+lr和 l t \boldsymbol l_t lt的 L 1 \boldsymbol L_1 L1或 L 2 \boldsymbol L_2 L2距离。
TransE采用最大间隔方法,定义了如下优化目标函数:
L = ∑ ( h , r , t ) ϵ S ∑ ( h ′ , r ′ , t ′ ) ϵ S − m a x ( 0 , f r ( h , t ) + γ − f r ′ ( h ′ , t ′ ) ) , L= \sum_{(h,r,t) \epsilon S} \sum_{(h',r',t') \epsilon S^- } max(0,f_r(h,t)+\gamma-f_{r'}(h',t')), L=(h,r,t)ϵS∑(h′,r′,t′)ϵS−∑max(0,fr(h,t)+γ−fr′(h′,t′)),
其中, S S S是合法三元组结合, S − S^- S−为错误三元组集合, γ γ γ为合法三元组得分与错误三元组之间的间隔距离。
错误三元组如何产生?TransE将 S S S中每个三元组的头实体、关系和尾实体中之一随机替换成其他实体或关系得到 S − S^- S−,即:
S − = { ( h ′ , r , t ) } ⋃ { ( h , r ′ , t ) } ⋃ { ( h , r , t ′ ) } . S^-={\{(h',r,t)}\}\bigcup{\{(h,r',t)}\}\bigcup{\{(h,r,t' )\}}. S−={(h′,r,t)}⋃{(h,r′,t)}⋃{(h,r,t′)}.
TransE模型的优点:参数少,计算复杂度低,能直接建立实体和关系之间的复杂语义联系。
Bordes等人在wordnet和freebase等数据集测试表明TransE模型较以往模型显著提升,特别是在大规模稀疏知识图谱其性能尤其惊人。
自TransE提出以来,大量研究工作对其进行扩展应用,其已经成为知识表示学习的代表模型。
知识表示学习的挑战和解决
复杂关系建模
TransE模型简单,但在处理知识库中的复杂关系时捉襟见肘。按照知识库中关系两端连接实体的数目,可以将关系划分为1-1,1-N,N-1和N-N四种类型。而TransE在处理后三种关系时性能显著降低。
为了解决这类问题,研究者提出了基于TransE的扩展模型。如TransH模型,TransR模型等。感兴趣的读者可参考原论文,这里不再列出其详细原理。
多源信息融合
多源信息融合是知识表示学习模型的重要挑战,大量的信息未被利用,如:
- 知识库中其它信息,如实体和关系的描述信息、类别信息等。
- 知识库外的海量信息,如互联网文本蕴含大量与知识库实体和关系有关的信息。
这些海量信息可以帮助提高知识表示的区分能力,改善数据稀疏问题。关于这个问题,有一些代表性工作。
DKRL(考虑实体描述的知识表示学习)模型
在文本表示阶段,其考虑2种模型:(1)CBOW模型,将文本中词向量简单相加作为文本表示;(2)利用卷积神经网络(CNN),能够考虑文本中的词序信息。
文本与知识融合的知识表示学习
Wang等人提出在表示学习中考虑文本数据,利用word2vec学习wikibaike中词表示,用TransE学习知识库中知识表示。同时利用wikibaike正文中的链接信息(锚文本与实体的对应关系),让文本中实体对应的词表示与知识库中的实体尽可能接近,从而实现文本与知识库融合的表示学习。
关系路径建模
PTransE模型。可被用来进行基于知识库的自动问答。详细参考原论文。
资源下载
关于知识表示的6篇论文合集下载地址,包括本文介绍的论文。
参考文献
[1] 刘知远,孙茂松,林衍凯,谢若冰. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2): 247-261.