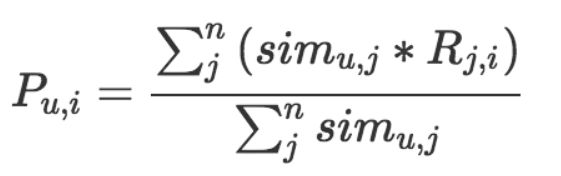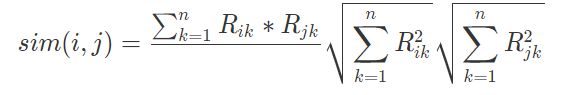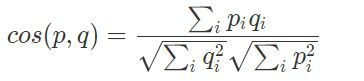推荐系统三十六式——学习笔记（三）

由于工作需要，开始学习推荐算法，参考【极客时间】->【刑无刀大牛】的【推荐系统三十六式】，学习并整理。

3 原理篇之紧邻推荐

3.1 协同过滤

要说提到推荐系统中，什么算法最名满天下，我想一定是协同过滤。在很多场合，甚至有人把协同过滤和推荐系统划等号，可见二者的关系多么紧密。

协同过滤的重点在于“协同”，所谓协同，也就是群体互帮互助，互相支持是集体智慧的体现，协同过滤也是这般简单直接，历久弥新。

当你的推荐系统度过了只能使用基于内容的推荐阶段后，就有了可观的用户行为了。这时候的用户行为通常是正向的，也就是用户或明或暗地表达着喜欢的行为。这些行为可以表达成一个用户和物品的关系矩阵，或者说网络、或者说是图，都是一个东西。

这个用户物品的关系矩阵中填充的就是用户对物品的态度，但并不是每个位置都有，需要的就是把那些还没有的地方填起来。这个关系矩阵是协同过滤的命根子，一切都围绕它来进行。

协同过滤是一个比较大的算法范畴。通常划分为两类：

1. 基于记忆的协同过滤（Memory-Based）；

基于记忆的协同过滤，就是记住每个人消费过什么东西，然后给他推荐相似的东西，或者推荐相似的人消费的东西。

2. 基于模型的协同过滤（Model-Based）。

基于模型的协同过滤则是从用户物品关系矩阵中去学习一个模型，从而把那些矩阵空白处填满。

3.2 基于用户的协同过滤

3.2.1 思想：详细来说就是：先根据历史消费行为帮你找到一群和你口味很相似的用户；然后根据这些和你很相似的用户再消费了什么新的、你没有见过的物品，都可以推荐给你。

这其实也是一个给用户聚类的过程，把用户按照兴趣口味聚类成不同的群体，给用户产生的推荐就来自这个群体的平均值；所以要做好这个推荐，关键是如何量化“口味相似”这个看起来很直接简单的事情。这关系到一个用户会跟哪些人在同一个房间内，万一进错了房间，影响就会不好。

3.2.2 原理：

核心是那个用户物品的关系矩阵，这个矩阵是最原始的材料。

第一步，准备用户向量，从这个矩阵中，理论上可以给每一个用户得到一个向量。

为什么要说是“理论上”呢？因为得到向量的前提是：用户爸爸需要在我们的产品里有行为数据，否则就得不到这个向量。这个向量有三个特点：

1. 向量的维度就是物品的个数；

2. 向量是稀疏的，也就是说并不是每个维度上都有数值，原因当然很简单，这个用户并不是消费过所有物品；

3. 向量维度上的取值可以是简单的 0 或者 1，也就是布尔值，1 表示喜欢过，0 表示没有，当然因为是稀疏向量，所以取值为 0 的就忽略了。

第二步，用每一个用户的向量，两两计算用户之间的相似度，设定一个相似度阈值或者设定一个最大数量，为每个用户保留与其最相似的用户。

第三步，为每一个用户产生推荐结果。

把和他“臭味相投”的用户们喜欢过的物品汇总起来，去掉用户自己已经消费过的物品，剩下的排序输出就是推荐结果，是不是很简单。具体的汇总方式我们用一个公式来表示：

等号左边就是计算一个物品 i 和一个用户 u 的匹配分数，

等号右边是这个分数的计算过程，分母是把和用户 u 相似的 n 个用户的相似度加起来，

分子是把这 n 个用户各自对物品 i 的态度，按照相似度加权求和。

这里的态度最简单就是 0 或者 1，1 表示喜欢过，0 表示没有，如果是评分，则可以是 0 到 5 的取值。
整个公式就是相似用户们的态度加权平均值。

3.2.3  实践

思考以下几个问题：

1. 只有原始用户行为日志，需要从中构造出矩阵，怎么做？

2. 如果用户的向量很长，计算一个相似度则耗时很久，怎么办？

3. 如果用户量很大，而且通常如此，两两计算用户相似度也是一个大坑，怎么办？

4. 在计算推荐时，看上去要为每一个用户计算他和每一个物品的分数，又是一个大坑，怎么办？

1、构造矩阵

我们在做协同过滤计算时，所用的矩阵是稀疏的，说人话就是：很多矩阵元素不用存，因为是 0。这里介绍典型的稀疏矩阵存储格式。

1. CSR：这个存储稍微复杂点，是一个整体编码方式。它有三个组成：数值、列号和行偏移共同编码。

2. COO：这个存储方式很简单，每个元素用一个三元组表示（行号，列号，数值），只存储有值的元素，缺失值不存储。

这些存储格式，在常见的计算框架里面都是标准的，如 Spark 中，Python 的 NumPy 包中。一些著名的算法比赛也通常都是以这种格式提供数据。这里不再赘述了。

把你的原始行为日志转换成上面的格式，就可以使用常用计算框架的标准输入了。

2、相似度计算

首先是单个相似度计算问题，如果碰上向量很长，无论什么相似度计算方法，都要遍历向量，如果用循环实现就更可观了，所以通常降低相似度计算复杂度的办法有两种：

1. 对向量采样计算。道理很简单，两个一百维的向量计算出的相似度是 0.7，我现在忍受一些精度的损失，不用 100 维计算，随机从中取出 10 维计算，得到相似度是 0.72，显然用 100 维计算出的 0.7 更可信一些，但是在计算复杂度降低十倍的情形下，0.72 和它误差也不大，后者更经济。这个算法由 Twitter 提出，叫做 DIMSUM 算法，已经在 Spark 中实现了。

2. 向量化计算。与其说这是一个小技巧，不如说这是一种思维方式。在机器学习领域，向量之间的计算是家常便饭，难道向量计算都要用循环实现吗？并不是，现代的线性代数库都支持直接的向量运算，比循环快很多。也就是我们在任何地方，都要想办法把循环转换成向量来直接计算，一般像常用的向量库都天然支持的，比如 Python 的 NumPy。

 

其次的问题就是，如果用户量很大，两两之间计算代价就很大。有两个办法来解决计算量太大的问题：

1. 第一个办法是：将相似度计算拆成 Map Reduce 任务，将原始矩阵 Map 成键为用户对，值为两个用户对同一个物品的评分之积，Reduce 阶段对这些乘积再求和，Map Reduce 任务结束后再对这些值归一化；

2. 第二个办法是：不用基于用户的协同过滤。

另外，这种计算对象两两之间的相似度的任务，如果数据量不大，一般来说不超过百万个，然后矩阵又是稀疏的，那么有很多单机版本的工具其实更快，比如 KGraph、 GraphCHI 等。

3、 推荐计算

得到了用户之间的相似度之后。接下来还有一个硬骨头，计算推荐分数。显然，为每一个用户计算每一个物品的推荐分数，计算次数是矩阵的所有元素个数，这个代价，你当然不能接受啊。这时候，你注意回想一下前面那个汇总公式，有这么几个特点我们可以来利用一下：

1. 只有相似用户喜欢过的物品需要计算，这个大大的赞，这个数量相比全部物品少了很多；

2. 把计算过程拆成 Map Reduce 任务。

拆 Map Reduce 任务的做法是：
1. 遍历每个用户喜欢的物品列表；
2. 获取该用户的相似用户列表；
3. 把每一个喜欢的物品 Map 成两个记录发射出去，一个是键为 < 相似用户 ID，物品 ID，1> 三元组，
    可以拼成一个字符串，值为 < 相似度 >，另一个是键为 < 相似用户 ID，物品 ID，0> 三元组，
    值为 < 喜欢程度 * 相似度 >，其中的 1 和 0 为了区分两者，在最后一步中会用到；
4. Reduce 阶段，求和后输出；
5. < 相似用户 ID，物品 ID, 0> 的值除以 < 相似用户 ID，物品 ID, 1> 的值

一般来说，中小型公司如果没有特别必要的话，不要用分布式计算，看上去高大上、和大数据沾上边了，实际上得不偿失。

拆分 Map Reduce 任务也不一定非要用 Hadoop 或者 Spark 实现。也可以用单机实现这个过程。

因为一个 Map 过程，其实就是将原来耦合的计算过程解耦合了、拍扁了，这样的话我们可以利用多线程技术实现 Map 效果。例如 C++ 里面 OpenMP 库可以让我们无痛使用多线程，充分剥削计算机所有的核。

4、一些改进

对于基于用户的协同过滤有一些常见的改进办法，改进主要集中在用户对物品的喜欢程度上：

1. 惩罚对热门物品的喜欢程度，这是因为，热门的东西很难反应出用户的真实兴趣，更可能是被煽动，或者无聊随便点击的情形，这是群体行为常见特点；

2. 增加喜欢程度的时间衰减，一般使用一个指数函数，指数就是一个负数，值和喜欢行为发生时间间隔正相关即可，这很好理解，小时候喜欢的东西不代表我现在的口味，人都是会变的，这是人性。

3.2.4  应用场景

基于用户的协同过滤有哪些应用场景。基于用户的协同过滤有两个产出：

1. 相似用户列表；

2. 基于用户的推荐结果。

所以我们不但可以推荐物品，还可以推荐用户！比如我们在一些社交平台上看到：“相似粉丝”“和你口味类似的人”等等都可以这样计算。

对于这个方法计算出来的推荐结果本身，由于是基于口味计算得出，所以在更强调个人隐私场景中应用更佳，在这样的场景下，不受大 V 影响，更能反应真实的兴趣群体，而非被煽动的乌合之众。

3.3  基于物品（Item-Based）的八卦

基于物品的协同过滤，通常也被叫作 Item-Based，因为后者更容易搜索到相关的文章，所以被更多地提及。

基于物品的协同过滤算法诞生于 1998 年，是由亚马逊首先提出的，并在 2001 年由其发明者发表了相应的论文（ Item-Based Collaborative Filtering Recommendation Algorithms ）。

这篇论文在 Google 学术上引用数已近 7000，并且在 WWW2016 大会上被授予了“时间检验奖”，颁奖词是：“这篇杰出的论文深深地影响了实际应用”。历经了 15 年后仍然在发光发热，这个奖它显然受之无愧。

虽然今天各家公司都在使用这个算法，好像它是一个公共资源一样，然而并不是这样，亚马逊早在 1998 年，也就是论文发表的三年前就申请了专利。

3.4 基于物品（Item-Based）原理

在基于物品的协同过滤出现之前，信息过滤系统最常使用的是基于用户的协同过滤。基于用户的协同过滤首先计算相似用户，然后再根据相似用户的喜好推荐物品，这个算法有这么几个问题：

1. 用户数量往往比较大，计算起来非常吃力，成为瓶颈；

2. 用户的口味其实变化还是很快的，不是静态的，所以兴趣迁移问题很难反应出来；

3. 数据稀疏，用户和用户之间有共同的消费行为实际上是比较少的，而且一般都是一些热门物品，对发现用户兴趣帮助也不大。

 

和基于用户的不同，基于物品的协同过滤首先计算相似物品，然后再根据用户消费过、或者正在消费的物品为其推荐相似的，基于物品的算法怎么就解决了上面这些问题呢？

首先，物品的数量，或者严格的说，可以推荐的物品数量往往少于用户数量；所以一般计算物品之间的相似度就不会成为瓶颈。

其次，物品之间的相似度比较静态，它们变化的速度没有用户的口味变化快；所以完全解耦了用户兴趣迁移这个问题。

最后，物品对应的消费者数量较大，对于计算物品之间的相似度稀疏度是好过计算用户之间相似度的。

根据我在上一篇文章中所说，协同过滤最最依赖的是用户物品的关系矩阵，基于物品的协同过滤算法也不能例外，它的基本步骤是这样的：

1. 构建用户物品的关系矩阵，矩阵元素可以是用户的消费行为，也可以是消费后的评价，还可以是对消费行为的某种量化如时间、次数、费用等；

2. 假如矩阵的行表示物品，列表示用户的话，那么就两两计算行向量之间的相似度，得到物品相似度矩阵，行和列都是物品；

3. 产生推荐结果，根据推荐场景不同，有两种产生结果的形式。一种是为某一个物品推荐相关物品，另一种是在个人首页产生类似“猜你喜欢”的推荐结果。不要急，稍后我会分别说。

3.5 计算物品相似度

前面较为笼统地说要计算物品之间的相似度，现在详细说说这块。从用户物品关系矩阵中得到的物品向量长什么样子呢？我来给你描述一下：

1. 它是一个稀疏向量；

2. 向量的维度是用户，一个用户代表向量的一维，这个向量的总共维度是总用户数量；

3. 向量各个维度的取值是用户对这个物品的消费结果，可以是行为本身的布尔值，也可以是消费行为量化如时间长短、次数多少、费用大小等，还可以是消费的评价分数；

4. 没有消费过的就不再表示出来，所以说是一个稀疏向量。

接下来就是如何两两计算物品的相似度了，一般选择余弦相似度，当然还有其他的相似度计算法方法也可以。计算公式如下：

用文字解释一下这个公式：
分母是计算两个物品向量的长度，求元素值的平方和再开方。
分子是两个向量的点积，相同位置的元素值相乘再求和。

这个公式的物理意义就是计算两个向量的夹角余弦值，相似度为 1 时，对应角度是 0，好比时如胶似漆，相似度为 0 时，对应角度为 90 度，毫不相干，互为路人甲。

1. 物品中心化。把矩阵中的分数，减去的是物品分数的均值；先计算每一个物品收到评分的均值，然后再把物品向量中的分数减去对应物品的均值。这样做的目的是什么呢？去掉物品中铁杆粉丝群体的非理性因素，例如一个流量明星的电影，其脑残粉可能会集体去打高分，那么用物品的均值来中心化就有一定的抑制作用。

2. 用户中心化。把矩阵中的分数，减去对应用户分数的均值；先计算每一个用户的评分均值，然后把他打过的所有分数都减去这个均值。

这样做的目的又是什么呢？每个人标准不一样，有的标准严苛，有的宽松，所以减去用户的均值可以在一定程度上仅仅保留了偏好，去掉了主观成分。

上面提到的相似度计算方法，不只是适用于评分类矩阵，也适用于行为矩阵。所谓行为矩阵，即矩阵元素为 0 或者 1 的布尔值，也就是在前面的专栏中讲过的隐式反馈。隐式反馈取值特殊，有一些基于物品的改进推荐算法无法应用，比如著名的 Slope One 算法。

3.6 计算推荐结果

在得到物品相似度之后，接下来就是为用户推荐他可能会感兴趣的物品了，基于物品的协同过滤，有两种应用场景。

第一种属于 TopK 推荐，形式上也常常属于类似“猜你喜欢”这样的。

出发方式是当用户访问首页时，汇总和“用户已经消费过的物品相似”的物品，按照汇总后分数从高到低推出。汇总的公式是这样的：

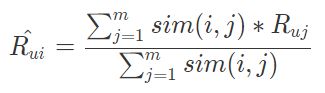   这个公式：核心思想就和基于用户的推荐算法一样，用相似度加权汇总。

要预测一个用户 u 对一个物品 i 的分数，遍历用户 u 评分过的所有物品，假如一共有 m 个，每一个物品和待计算物品 i 的相似度乘以用户的评分，这样加权求和后，除以所有这些相似度总和，就得到了一个加权平均评分，作为用户 u 对物品 i 的分数预测。

和基于物品的推荐一样，我们在计算时不必对所有物品都计算一遍，只需要按照用户评分过的物品，逐一取出和它们相似的物品出来就可以了。

这个过程都是离线完成后，去掉那些用户已经消费过的，保留分数最高的 k 个结果存储。当用户访问首页时，直接查询出来即可。

第二种属于相关推荐，也就是我们今天专栏题目所指的场景。

这类推荐不需要提前合并计算，当用户访问一个物品的详情页面时，或者完成一个物品消费的结果面，直接获取这个物品的相似物品推荐，就是“看了又看”或者“买了又买”的推荐结果了。

3.7 Slope One 算法

经典的基于物品推荐，相似度矩阵计算无法实时更新，整个过程都是离线计算的，而且还有另一个问题，相似度计算时没有考虑相似度的置信问题。例如，两个物品，他们都被同一个用户喜欢了，且只被这一个用户喜欢了，那么余弦相似度计算的结果是 1，这个 1 在最后汇总计算推荐分数时，对结果的影响却最大。

Slope One 算法针对这些问题有很好的改进。在 2005 年首次问世，Slope One 算法专门针对评分矩阵，不适用于行为矩阵。Slope One 算法计算的不是物品之间的相似度，而是计算的物品之间的距离，相似度的反面。举个例子就一目了然，下面是一个简单的评分矩阵：

↑ 这个矩阵反应了这些事实：用户 1 给物品 A、B、C 都评分了，分别是 5，3，2；用户 2 给物品 A、B 评分了，分别是 3、4；用户 3 给物品 B、C 评分了，分别是 2、5。

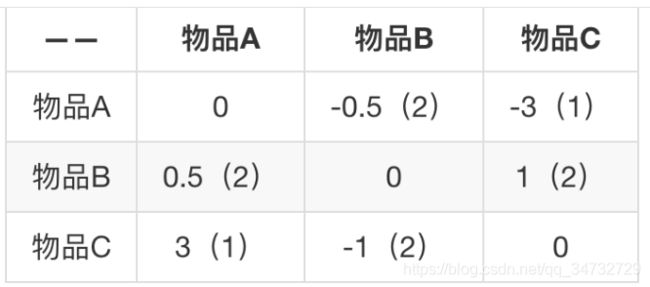
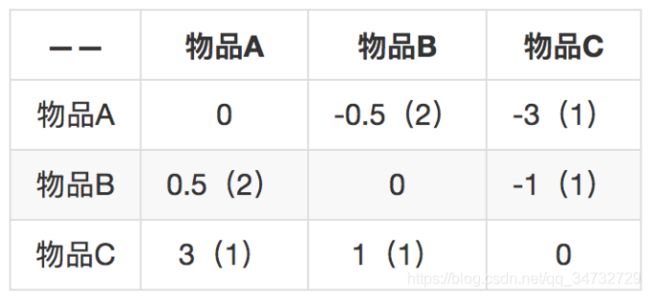
现在首先来两两计算物品之间的差距：

A和B的差距： (（5+3）-（3+4）)/2 = 0.5；
A和C的差距：（5-2）/1 = 3;
B和A的差距：（（3+4）-（5+3））/2 = -0.5;
B和C的差距：（（3+2）-（2+5））/2 = -1;
C和A的差距：（2-5）/1 = -3;
C和B的差距：（（2+5）-（3+2））/2 = 1；

括号里表示两个物品的共同用户数量，代表两个物品差距的置信程度。比如物品 A 和物品 B 之间的差距是 0.5，共同用户数是 2，反之，物品 B 和物品 A 的差距是 -0.5，共同用户数还是 2。知道这个差距后，就可以用一个物品去预测另一个物品的评分。

如果只知道用户 3 给物品 B 的评分是 2，那么预测用户 3 给物品 A 的评分呢就是 2.5，因为从物品 B 到物品 A 的差距是 0.5。

在此基础上继续推进，如果知道用户给多个物品评分了，怎么汇总这些分数呢？

方法是把单个预测的分数按照共同用户数加权求平均。比如现在知道用户 3 不但给物品 B 评分为 2，还给物品 C 评分为 5，物品 B 对物品 A 的预测是 2.5 分，刚才计算过了，物品 C 给物品 A 的预测是 8 分，再加权平均。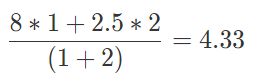

3.8 相似度的本质

推荐系统中，推荐算法分为两个门派，一个是机器学习派，另一个就是相似度门派。机器学习派是后起之秀，而相似度派则是泰山北斗，以致撑起来推荐系统的半壁江山。

近邻推荐顾名思义就是在地理位置上住得近。如果用户有个邻居，那么社交软件上把邻居推荐给他在直观上就很合理，当然，如果邻居姓王的话，就不要推荐了。

这里说的近邻，并不一定只是在三维空间下的地理位置的近邻，在任意高维空间都可以找到近邻，尤其是当用户和物品的特征维度都很高时，要找到用户隔壁的邻居，就不是那么直观，需要选择好用适合的相似度度量办法。

近邻推荐的核心就是相似度计算方法的选择，由于近邻推荐并没有采用最优化思路，所以效果通常取决于矩阵的量化方式和相似度的选择。

相似度，与之配套的还有另一个概念就是距离，两者都是用来量化两个物体在高维空间中的亲疏程度的，它们是硬币的两面。

推荐算法中的相似度门派，实际上有这么一个潜在假设：如果两个物体很相似，也就是距离很近，那么这两个物体就很容易产生一样的动作。

如果两篇新闻很相似，那么他们很容易被同一个人先后点击阅读，如果两个用户很相似，那么他们就很容易点击同一个新闻。这种符合直觉的假设，大部分时候很奏效。

其实属于另一门派的推荐算法——机器学习中，也有很多算法在某种角度看做是相似度度量。

例如，逻辑回归或者线性回归中，一边是特征向量，另一边是模型参数向量，两者的点积运算，就可以看做是相似度计算，只不过其中的模型参数向量值并不是人肉指定的，而是从数据中由优化算法自动总结出来的。

在近邻推荐中，最常用的相似度是余弦相似度。然而可以选用的相似度并不只是余弦相似度，还有欧氏距离、皮尔逊相关度、自适应的余弦相似度、局部敏感哈希等。使用场景各不相同，今天，我会分别一一介绍如下。

3.9 相似度计算方法

3.9.1 数据分类

相似度计算对象是向量，或者叫做高维空间下的坐标，一个意思。那表示这个向量的数值就有两种：

1.实数值；

2. 布尔值，也就是 0 或者 1。

1、欧氏距离

两个物体，都在同一个空间下表示为两个点，假如叫做 p 和 q，分别都是 n 个坐标。那么欧式距离就是衡量这两个点之间的距离，从 p 到 q 移动要经过的距离。欧式距离不适合布尔向量之间。

显然，欧式距离得到的值是一个非负数，最大值是正无穷。通常相似度计算度量结果希望是 [-1，1] 或者 [0，1] 之间，所以欧式距离要么无法直接使用到这个场景中，要么需要经过二次转化得到 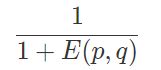     (0, 1)

2、余弦相似度

大名鼎鼎的余弦相似度，度量的是两个向量之间的夹角，其实就是用夹角的余弦值来度量，所以名字叫余弦相似度。当两个向量的夹角为 0 度时，余弦值为 1，当夹角为 90 度时，余弦值为 0，为 180 度时，余弦值则为 -1。

余弦相似度在度量文本相似度、用户相似度、物品相似度的时候都较为常用；但是在这里需要提醒你一点，余弦相似度的特点：它与向量的长度无关。因为余弦相似度计算需要对向量长度做归一化：

经过向量长度归一化后的相似度量方式，背后潜藏着这样一种思想：两个向量，只要方向一致，无论程度强弱，都可以视为“相似”。

比如，我用 140 字的微博摘要了一篇 5000 字的博客内容，两者得到的文本向量可以认为方向一致，词频等程度不同，但是余弦相似度仍然认为他们是相似的。

在协同过滤中，如果选择余弦相似度，某种程度上更加依赖两个物品的共同评价用户数，而不是用户给予的评分多少。这就是由于余弦相似度被向量长度归一化后的结果。

余弦相似度对绝对值大小不敏感这件事，在某些应用上仍然有些问题。

举个小例子，用户 A 对两部电影评分分别是 1 分和 2 分，用户 B 对同样这两部电影评分是 4 分和 5 分。用余弦相似度计算出来，两个用户的相似度达到 0.98。这和实际直觉不符，用户 A 明显不喜欢这两部电影。

针对这个问题，对余弦相似度有个改进，改进的算法叫做调整的余弦相似度（Adjusted Cosine Similarity）。调整的方法很简单，就是先计算向量每个维度上的均值，然后每个向量在各个维度上都减去均值后，再计算余弦相似度。

前面这个小例子，用调整的余弦相似度计算得到的相似度是 -0.1，呈现出两个用户口味相反，和直觉相符。

3、皮尔逊相关度

皮尔逊相关度，实际上也是一种余弦相似度，不过先对向量做了中心化，向量 p 和 q 各自减去向量的均值后，再计算余弦相似度。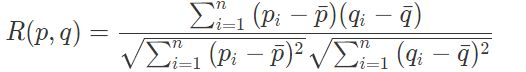

皮尔逊相关度计算结果范围在 -1 到 1。-1 表示负相关，1 比表示正相关。皮尔逊相关度其实度量的是两个随机变量是不是在同增同减。

如果同时对两个随机变量采样，当其中一个得到较大的值另一也较大，其中一个较小时另一个也较小时，这就是正相关，计算出来的相关度就接近 1，这种情况属于沆瀣一气，反之就接近 -1。

由于皮尔逊相关度度量的时两个变量的变化趋势是否一致，所以不适合用作计算布尔值向量之间相关度，因为两个布尔向量也就是对应两个 0-1 分布的随机变量，这样的随机变量变化只有有限的两个取值，根本没有“变化趋势，高低起伏”这一说。

4、杰卡德（Jaccard）相似度

杰卡德相似度，是两个集合的交集元素个数在并集中所占的比例。由于集合非常适用于布尔向量表示，所以杰卡德相似度简直就是为布尔值向量私人定做的。对应的计算方式是：

1. 分子是两个布尔向量做点积计算，得到的就是交集元素个数；

2. 分母是两个布尔向量做或运算，再求元素和。

余弦相似度适用于评分数据，杰卡德相似度适合用于隐式反馈数据。例如，使用用户的收藏行为，计算用户之间的相似度，杰卡德相似度就适合来承担这个任务。