差分进化算法(DE)简介及Python实现
一、概述
差分进化算法(Differential Evolution,DE)由Storn和Price于1995年首次提出,主要用于求解实数优化问题。1996年在日本名古屋举行的第一届国际演化计算(ICEO)竞赛中,差分进化算法被证明是速度最快的进化算法。
差分进化思想来源于遗传算法(GeneticAlgorithm,GA),模拟遗传学中的杂交(crossover)、变异(mutation)、复制(reproduction)来设计遗传算子。该算法是一类基于群体的自适应全局优化算法,属于演化算法的一种。差分进化算法具有结构简单、容易实现、收敛快速、鲁棒性强等特点,被广泛应用在数据挖掘、模式识别、数字滤波器设计、人工神经网络、电磁学等各个领域。
差分进化算法相对于遗传算法而言,相同点都是通过随机生成初始种群,以种群中每个个体的适应度值为选择标准,主要过程也都包括变异、交叉和选择三个步骤。不同之处在于遗传算法是根据适应度值来控制父代杂交,变异后产生的子代被选择的概率值,在最大化问题中适应值大的个体被选择的概率相应也会大一些。而差分进化算法变异向量是由父代差分向量生成,并与父代个体向量交叉生成新个体向量,直接与其父代个体进行选择。显然差分进化算法相对遗传算法的逼近效果更加显著。
二、差分进化算法
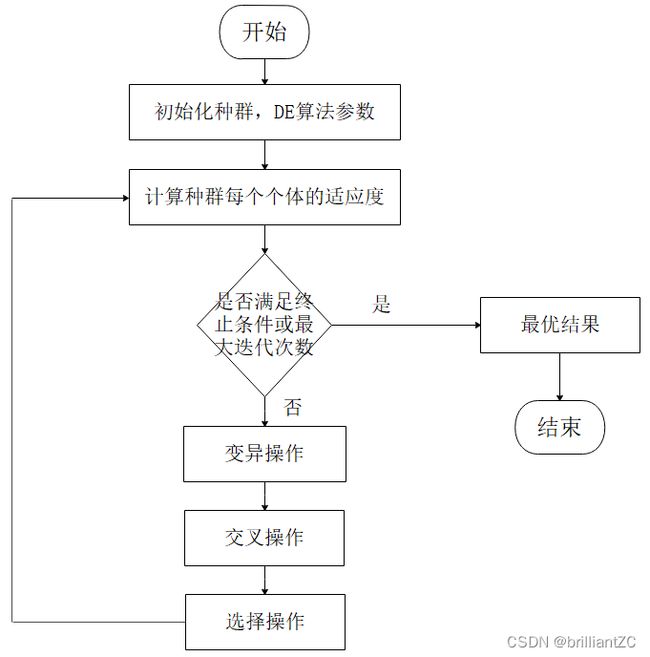
一、算法的主要流程:
1、初始化种群
在解空间中随机均匀产生M个个体,每个个体由n维向量组成
X i ( 0 ) = ( x i , 1 ( 0 ) , x i , 2 ( 0 ) , . . . . , x i , n ( 0 ) ) i = 1 , 2 , . . . , M \begin{aligned} X_i(0) = (x_i,_1(0),x_i,_2(0),....,x_i,_n(0)) \\ i = 1,2,...,M \end{aligned} Xi(0)=(xi,1(0),xi,2(0),....,xi,n(0))i=1,2,...,M
第i个个体的第j维值初始化方式如下:
X i , j ( 0 ) = L j − m i n + r a n d ( 0 , 1 ) ( L j − m a x − L j − m i n ) i = 1 , 2 , . . . , M j = 1 , 2 , 3 , . . . , n \begin{aligned} X_i,_j(0) = L_{j-min} + rand(0,1) (L_{j-max} - L_{j-min}) \\ i = 1,2,...,M\\ j=1,2,3,...,n \end{aligned} Xi,j(0)=Lj−min+rand(0,1)(Lj−max−Lj−min)i=1,2,...,Mj=1,2,3,...,n
2、变异操作
差分进化算法与遗传算法最显著的区别在于DE的个体变异是通过差分策略实现的
在第g次迭代中,从种群中随机选择3个个体Xp1(g),Xp2(g),Xp3(g),且p1≠p2≠p3≠i,生成的变异向量为:
H i ( g ) = X p 1 ( g ) + F ⋅ ( X p 2 ( g ) − X p 3 ( g ) ) \begin{aligned} H_i(g)=X_{p1}(g)+F⋅(X_{p2}(g)−X_{p3}(g)) \end{aligned} Hi(g)=Xp1(g)+F⋅(Xp2(g)−Xp3(g))
其中 F是缩放因子,F越大,越不容易陷入局部极值点;F越小,越有利于收敛到局部极值点。
3、交叉操作
以一定概率让新产生的变异个体与原种群中个体进行交叉重组,增强种群的多样性
v i , j = { h i , j ( g ) , r a n d ( 0 , 1 ) ≤ c r x i , j ( g ) , e l s e v_i,_j=\left\{ \begin{matrix} h_i,_j(g),rand(0,1)≤cr \\ x_i,_j(g),else \end{matrix} \right. vi,j={hi,j(g),rand(0,1)≤crxi,j(g),else
其中cr∈[0,1]为交叉概率
4、选择操作
不是在所有的Vi ( g ), X_i(g)的总共2M个个体中选出适应度最高的那M个个体,而是对于这一代的每个个体的Vi( g ) 和Xi ( g )都进行一次判断,留下适应度最好的那个作为下一代同样位置上的个体。
X i ( g + 1 ) = { V i ( g ) , f ( V i ( g ) ) < f ( X i ( g ) ) X i ( g ) , e l s e X_i(g+1)=\left\{ \begin{matrix} V_i(g),f(V_i(g))
对于每个个体, Xi(g+1)要好于或持平于 Xi(g)。
二、算法步骤
step1:确定差分进化算法控制参数,确定适应度函数。差分进化算法控制参数包括:种群大小NP、缩放因子F与杂交概率CR。
step2:随机产生初始种群。
step3:对初始种群进行评价,即计算初始种群中每个个体的适应度值。
step4:判断是否达到终止条件或进化代数达到最大。若是,则终止进化,将得到最佳个体作为最优解输出;若否,继续。
step5:进行变异和交叉操作,得到中间种群。
step6:在原种群和中间种群中选择个体,得到新一代种群。
step7:进化代数g=g+1,转step4。
- 种群规模(M):一般介于5n到10n之间,但不能少于4,否则变异算则无法进行.
- 缩放因子(F):F主要影响算法的全局寻优能力。F越小,算法对局部的搜索能力更好,F越大算法越能跳出局部极小点,但是收敛速度会变慢。此外,F还影响种群的多样性。F一般取[0,2],通常取0.5
- 交叉概率(cr):反映的是在交叉的过程中,子代与父代、中间变异体之间交换信息量的大小程度。CR的值越大,信息量交换的程度越大。反之,如果CR的值偏小,将会使种群的多样性快速减小,不利于全局寻优。cr一般取[0,1],通常取0.3。CR越大,收敛速度越快,但易发生早熟现象
三、python实现
import numpy as np
POPULATION = 10 # 种群数
F = 0.7 # 差分缩放因子
P_CROSS = 0.9 # 交叉概率
MAX_ITER = 50 # 最大迭代次数
lb = np.array([-10]) # 下限
ub = np.array([10]) # 上限
# 目标函数
def obj_fun(u):
f = np.cos(u) * np.exp(-(u - np.pi) ** 2)
return f[0]
# 初始化种群
s = np.zeros((POPULATION,len(lb)))
fitness = np.zeros(POPULATION)
for i in range(POPULATION):
s[i] = lb + (ub - lb) * np.random.rand(len(lb))
fitness[i] = obj_fun(s[i])
i = 0
f_opt = np.min(fitness)
u_opt = s[np.argmin(fitness)]
while i < MAX_ITER:
i += 1
# 随机选取两个变量进行突变
k = np.random.randint(0,POPULATION,2)
v = s + F * (s[k[0]]-s[k[1]])
# 超过范围的进行约束
for x in v:
for p in range(len(x)):
if(x[p] > ub[p]):
x[p] = ub[p]
if(x[p] < lb[p]):
x[p] = lb[p]
# 交叉
is_cross = np.random.rand(POPULATION * len(lb)).reshape((POPULATION,len(lb))) < P_CROSS
v = s * (1 - is_cross) + v * is_cross
# 新生的的比原来的好就进行替换
for p in range(POPULATION):
f_new = obj_fun(v[p])
if(f_new <= fitness[p]):
s[p] = v[p]
fitness[p] = f_new
if(f_new <= f_opt):
f_opt = f_new
u_opt = v[p]
print(u_opt,f_opt,sep='\t')
print(u_opt)
print(f_opt)