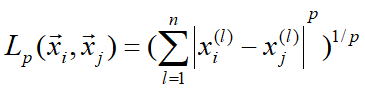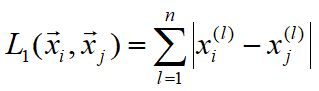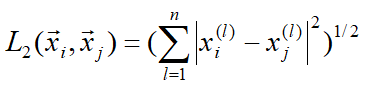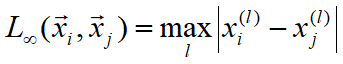机器学习——k近邻算法

算法介绍

k近邻法(k-nearest neighbors)是由Cover和Hart于1968年提出的，它是懒惰学习(lazy learning)的著名代表。

k近邻算法简单、直观：给定一个训练数据集（其中的实例类别已定），对新的输入实例，在训练数据集中找到与该实例最接近的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。

举个栗子

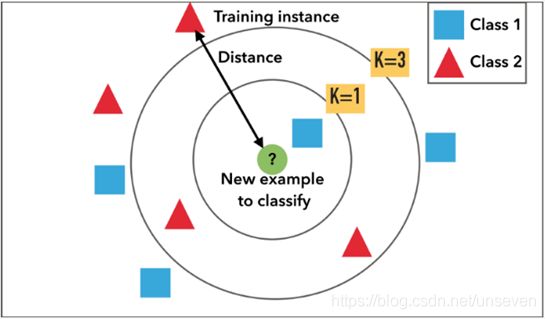
1.给定了红色和蓝色的训练样本，绿色为测试样本
2.计算绿色点到其他点的距离
3.选取离绿点最近的k个点
4.选取k个点中，同种颜色最多的类。
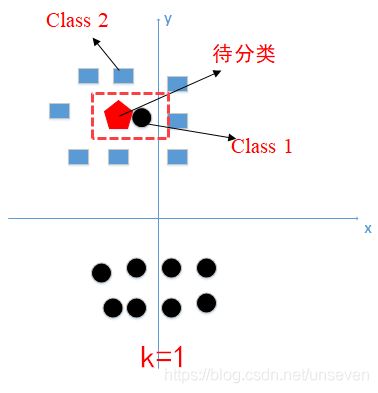
例如：k=1时，k个点全是蓝色，那预测结果就是Class 1；
k=3时，k个点中两个红色一个蓝色，那预测结果就是Class 2

要素1：k值的选取

1. k值过小，模型复杂，易过拟合
   
   如果k太小，如1，则模型太复杂，容易学习到噪声，非常容易判定为噪声类别。换个简单的说法，当k=1时，如果离测试点距离最近的是一个噪声值（无用数据），那么判断就会出错。

过拟合：在训练集上准确率非常高，而在测试集上准确率低。即：平时学习很好，考试很差；比如平时做的都是线性代数，但却是去考概率论。

2. k值过大，模型简单，易预测错误
   可以想象，如果K的值大到全部的训练集，那么判断就会变成一个简单的比谁的个数多，如果A种类的个数最多，那么毫无疑问的无论放的测试点是B，还是C，都会被判定为A

3. k值既不能过大，又不能过小，那么如何选取k值
   解决办法：交叉验证

交叉验证：将原始数据进行分组,一部分做为训练集另一部分做为验证集,首先用训练集对分类器进行训练,在利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标.

举个栗子

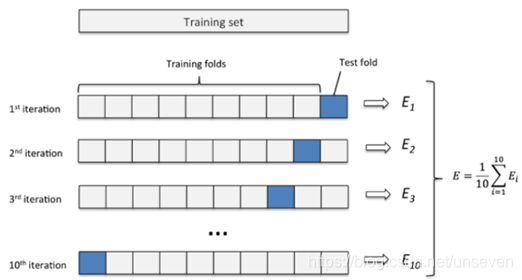
我们把样本分成十等分，第一次取第十份为测试集，前九份为训练集；第二次取第九份为测试集，其余为训练集…然后k取1，2，3…测出最合适的k值

要素2：距离度量

1. Lp距离
   

2. p=1时，曼哈顿距离
   

3. p=2时，欧氏距离
   

4. p=∞时，为各维度距离中的最大值
   

归一化特征值的必要性

要素3：分类决策规则

多采用表决，也可基于距离远近进行加权投票

多数表决规则等价于经验风险最小化。
常用误分类率评价KNN性能，要使误分类率最小，即经验风险最小，需使得正确分类率最大，即多数表决：

误分类率：

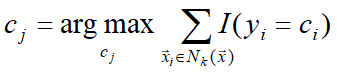
k近邻算法

k近邻法的分类算法描述步骤：

（1）输入：训练数据集为实例的特征向量
	T={((1) ⃗,1),((2) ⃗,2),…,(() ⃗,)}，
 	 ⃗_∈⊆ℝ为实例的特征向量，_∈={c1,c2,…,ck}为实例的类别，
	 i=1,2,…,N。给定实例特征向量 ⃗。
 （2）输出：实例 ⃗所属类别y。
 （3）其实现步骤为：
	根据给定的距离度量，在T中寻找与 ⃗最近邻的k个点，
	定义涵盖这k个点的 ⃗的邻域记作Nk( ⃗)。
	从Nk( ⃗)中，根据分类决策规则决定 ⃗的类别：

说简单点就是，在很多点组成的训练集里，放入一个新的点，测试该点属于什么种类，把所有点和该点算一个距离按距离排序，取前k个点，k个点中哪个类别的个数最多，我们就认为这个点也是这一类。

python代码

k近邻算法

def classify0(inX, dataSet, labels, k):
    # 用于分类的输入向量是inX，输入的训练样本集为dataSet,标签向量为labels，最后的参数k表示选择邻居的数目
    # 标签向量的元素数目和矩阵dataSet的行数相同
    dataSetSize = dataSet.shape[0]  # shape的功能是读取矩阵的长度，比如shape[0]就是读取矩阵第一维度的长度
    diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet  # tile(a,(x,y))将a在行重复x次，在列上重复y次
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)# numpy中的sum函数，输入可以是列表，元组，数组。对于数组可以指定维度进行相加。默认为axis=none，sum将所有的元素相加
    distances = sqDistances**0.5
    sortedDistIndicies = distances.argsort() # 将元素从小到大排列，提取其对应的index(索引)，然后输出给sortedDistIndicies，记录的是下标
    classCount = {} # 字典
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)  # key是一个函数，reverse=True是倒序，由大到小
    return sortedClassCount[0][0]

归一化特征值

def autoNorm(dataSet):   # 归一化特征值
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = np.zeros(np.shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    normDataSet = normDataSet/np.tile(ranges, (m, 1))   #element wise divide
    return normDataSet, ranges, minVals

k近邻算法优缺点

1. 优点
   精度高，对异常值不敏感，无数据输入假定
2. 缺点
   计算复杂度高，空间复杂度高
   如果仅数据集就几十上百G，还每个点都算距离，显然复杂度很高，T(kn)

对KNN算法进行改进，于是有了之后的kd树算法，树形结构的复杂度(klog2 n)要低的多