网络模型int8量化中使用的一些量化方法
1. 概述
前言:这篇博客中涉及到的是网络在做int8 infer时候涉及到的量化方法,这里并不涉及到int8训练的东西,这篇文章涉及到的量化方法主要来自于:Quantizing deep convolutional networks for efficient inference: A whitepaper。
深度学习中网络的加速主要有如下的几种方式:
- 1)设计高效且小的网络,如MobileNet系列、shuffleNet系列、VoVNet等;
- 2)从大的模型开始通过量化、剪裁、蒸馏等压缩技术实现网络的小型化;
- 3)在inference阶段使用特殊的计算库实现计算的加速,比如MKL、TensorRT等;
在上面的方法中最简单的方法就是降低模型运算过程中的bits数量,降低到16bits、8bits甚至2bits。这样做具有如下的优点:
- 1)在众多的使用场合与模型中可以广泛使用,并不需要设计再设计特殊的网络结构,而且量化是从训练好的模型上进行的,并不需要重训练,且损失精度比较少。目前现有的大部分硬件计算资源都是支持这样的运算模式的,因而也不需要重新设计专门的硬件;
- 2)模型量化可以显著减少模型的尺寸大小,理论上可以减少模型的尺寸4倍,并且模型的性能损失很小;
- 3)使用更低bits数的模型可以减少在运算过程中的内存与缓存消耗;
- 4)大多数的处理器对8bits的运算更快;
- 5)8bits的计算拥有更好的实现效率,因而进行对应的计算所消耗的能量更少;
2. 量化的方法
2.1 Uniform Affine Quantizer
将范围在 ( x m i n , x m a x ) (x_{min},x_{max}) (xmin,xmax)之间的浮点数字映射到规定的范围 ( 0 , N l e v e l s − 1 ) , N l e v e l s = 256 f o r 8 b i t s (0,N_{levels}-1),N_{levels}=256\ for\ 8\ bits (0,Nlevels−1),Nlevels=256 for 8 bits。这是需要特殊指定两个参数:映射步长比 Δ \Delta Δ(Scale),映射的零点 z z z(Zero-point),其中映射的零点是很关键的,以排除像0值padding对量化造成的错误。
对于单侧的分布,浮点分布 ( x m i n , x m a x ) (x_{min},x_{max}) (xmin,xmax)会被映射去包含0点。例如将范围为 ( 2.1 , 3.5 ) (2.1,3.5) (2.1,3.5)映射到 ( 0 , 3.5 ) (0,3.5) (0,3.5),这样就可能会导致精度的损失。
在Scale与Zero-point确定之后,量化的正向运算可以描述为:
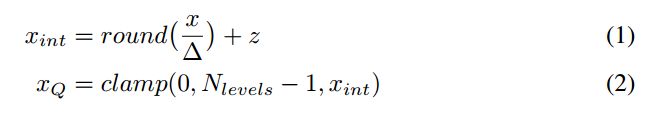
其中的 c l a m p clamp clamp操作被描述为:

那么对应的反向操作则是:

2.2 Uniform symmetric quantizer
这个量化算法将上面量化算法中的零点直接设置为: z = 0 z=0 z=0,从而方便了计算。因而前向的量化过程可以描述为:

对于反向的过程描述为:
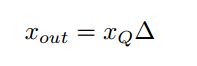
2.3 Stochastic quantizer
这个量化方法是在前面第一个量化方法的基础上引入服从 ( − 1 2 , 1 2 ) (-\frac{1}{2},\frac{1}{2}) (−21,21)上均匀分布的变量,从而其量化过程可以描述为:
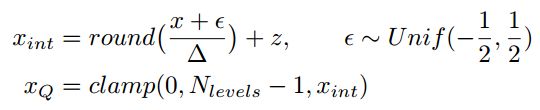
这样做的好处是使得在计算梯度的时候具有良好的性质,但是这样的量化方法在inference的时候对现有的硬件兼容不是很好。
3. 训练好的模型上的量化
对于已经训练好的模型进行量化的方式有两种:只量化权重和量化权重和激活。这两种量化策略在下面的内容会讲到。文中经过证实采用逐通道(per-channel)与非对称范围的量化的模型精度与浮点型是比较接近的。
3.1 只量化权值
只量化权值是只将权值数据量化到8bits上,因而不需要量化校准集。这样量化方式只适用于对性能要求不高且要求模型大小比较高的场景下,这种方法一般不予以采纳。
3.2 权重与激活量化
这里除了对权重参数进行per-channel的量化之外,还需要额外准备校准数据集,以提供对激活的量化参数的确定,这样的方法其量化的结果也是比较好的。在TensorRT中也是采用了这样的量化方式进行网络的量化技术,也达到了很不错的性能。
3.3 量化性能对比
只量化权重对性能的影响,其中包含量化粒度的对比(per-channel、per-layer):

权重与激活都量化对于性能的影响:
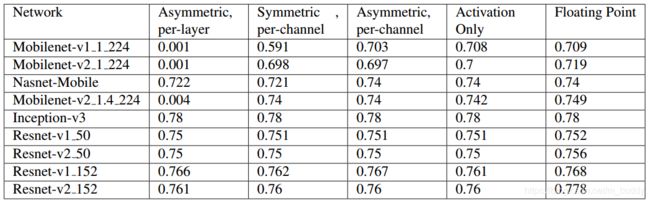
基于上述实验结果,得到如下的结论:
- 1)Per-channel的权值量化与activation量化可以使得量化之后的模型与浮点型运算得到的结果相差尽量减小;
- 2)activation的量化可以有效减少精度上的损失,下面的这几个操作会使得activation的范围较小:(a)在batchnorm之后没有添加scale;(b)ReLU6将激活之后的值限定在 ( 0 , 6 ) (0,6) (0,6)的范围内。
- 3)拥有更多参数的模型,例如ResNet与Inception-V3,其量化的鲁棒性是好于参数少的模型的;
- 4)当权重在层的粒度(非channel)上被量化时,会有很大的性能下降(这主要是由于batchnorm导致的数值波动),特别对于MobileNet网络;
- 5)大多数情况下由量化引入的性能下降是由于权值的量化过程;