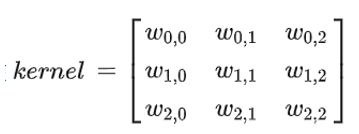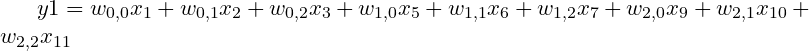反卷积理解和推导

参考 怎样通俗易懂地解释反卷积？ - 知乎，【基础知识学习】卷积与反卷积学习笔记 - 知乎

1.概念

反卷积是一种特殊的正向卷积，先按照一定的比例通过补 0 来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

图1 反卷积原理图（stride=1）

 图1 反卷积原理图（stride=2）

2.数学推导

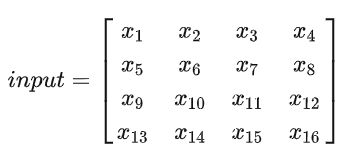
假设输入图像 input 尺寸为 4×4 ，元素矩阵为：

卷积核 kernel 尺寸为 3×3 ，元素矩阵为：

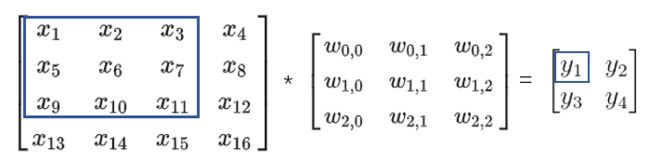
步长 strides=1，填充 padding=0，即 i=4，k=3，s=1，p=0，按照卷积公式， ，输出图像 output 的尺寸为 2×2。

其中，

把 input 的元素矩阵展开成一个列向量 X：

把输出图像 output 的元素矩阵展开成一个列向量 Y：

对于输入的元素矩阵 X 和 输出的元素矩阵 Y ，用矩阵运算描述这个过程：

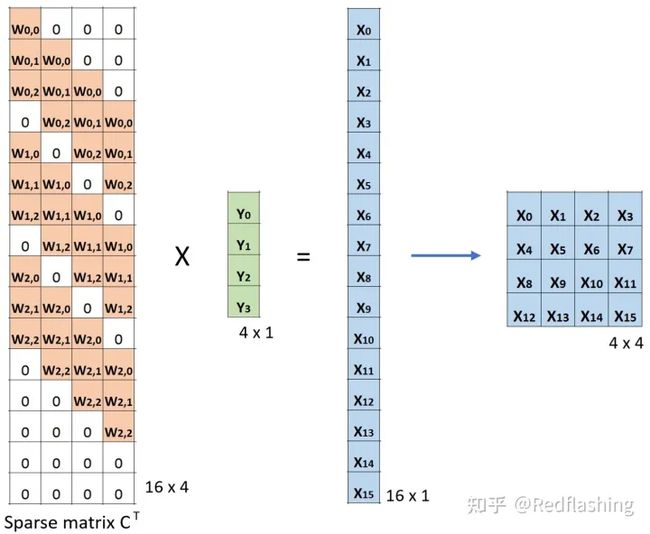
通过推导，我们可以得到稀疏矩阵 C ：

用C的第一行和input相乘，得到y1; 第二行和input相乘，得到y2......

反卷积的操作就是要对这个矩阵运算过程进行逆运算，即 

---

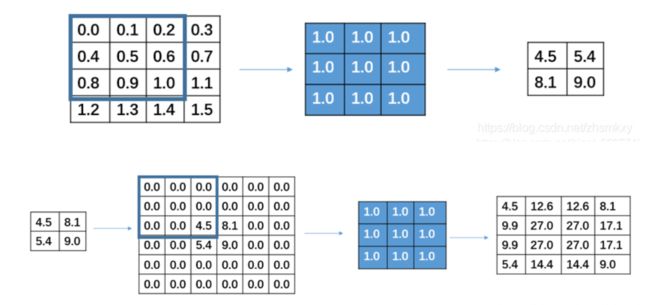
下面这个图直观地体现出整个过程：

将输入input 平展成 16∗1 矩阵，将卷积核转换为一个 4x16 的稀疏矩阵。然后，进行矩阵乘法。将所得到的 4x1 矩阵reshape为 2x2 输出。

此时，若用卷积核对应稀疏矩阵的转置（16∗4）乘以输出的平展（4∗1），得到的结果（16∗1）的形状和输入的形状（16∗1）相同。 

 注：上述两次操作并不是可逆关系，对于同一个卷积核，转置卷积的操作并不能恢复到原始的数值，而仅仅保留原始的形状。

如上图所示，我们用一个3×3的卷积核卷积一个4×4的输入，得到一个2×2的输出后，再进行反卷积，发现并不是原来的输入。其实很简单，第一个数相当于9个数相加等于4.5，用一个方程怎么可能解出9个未知数。所以反卷积不能还原原来的输入，只能保证shape相同。 

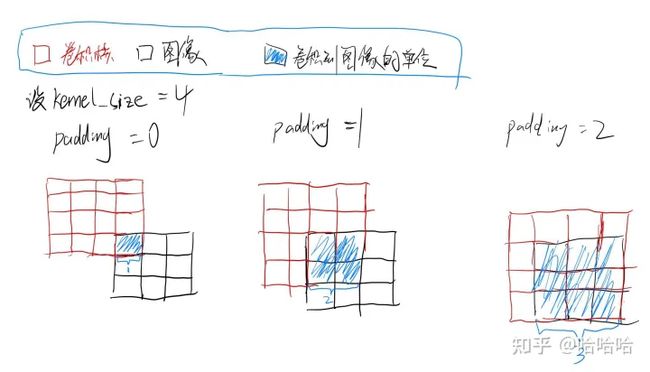
3.padding

1.卷积中padding

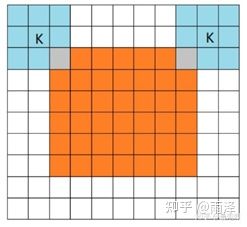
①full模式下从卷积核与图像相交点处开始做卷积：

②same模式下为卷积核中心点与图像重合时开始卷积，也叫half填充：

③valid 下为卷积核完全在图像中的卷积：

2.反卷积中的padding

一种说法是：直观上填充0的层数 padding。

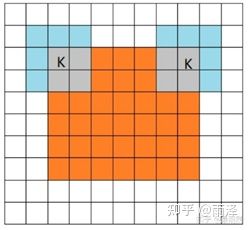
一种说法是：卷积核初始时卷积图像的尺寸，当padding’=0时，初始卷积核可卷积到图像的单位等于1，参考官网 ConvTranspose2d — PyTorch 1.13 documentation ，看图理解：

它们的关系是 padding’=kernel-1-padding。

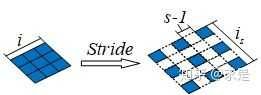
4.stride

1.卷积中的stride: 卷积核卷积的步长

2.反卷积中的stride: 图像的每个像素之间的距离，即给像素之间添加stride-1个元素0。

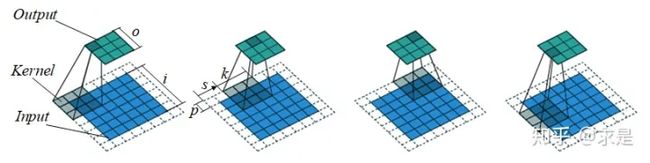
5.输出图像尺寸公式

1.卷积的输出图像大小

以上图为例，设input=6，kernel=3，stride=2，padding=1，则output=[(6+2-3)/2+1]=[3.5]=3

2.反卷积的输出图像大小

注：此公式中的padding是外层填充0的层数。

反卷积中，stride就是在相邻元素之间添加stride-1个0元素。 变换后，实际的input大小

假设输入图片大小为3x3，其他参数和之前一样kernel=3，padding=1，stride=2。

注：反卷积的stride是用在扩展输入图像上的，而不是kernel移动的步长，所以反卷积中kernel步长永远是1。

计算得，o=[(3+1*2+2-3)/1+1]=5，即输出尺寸等于5。

---

注：如果padding定义成卷积核初始时卷积图像的尺寸，那反卷积的公式应该为

相当于把 p 用 p'=k-1-p 替换掉。

---

3.例题

注：此公式中的padding是外层填充0的层数。

1.输入尺寸input=2，kernel_size=3,stride=1,padding=2，计算反卷积的输出尺寸？

is=i+(s-1)(i-1)=i=2

output= (is+2p-k)/1+1=(2+4-3)/1+1=4

---

2.输入尺寸input=3,kernel=3,stride=2,padding=1，计算反卷积的输出尺寸？

is=i+(s-1)(i-1)=3+1*2=5

output= (is+2p-k)/1+1=(5+2-3)/1+1=5