正态分布（高斯分布）、Q函数、误差函数、互补误差函数（定义，意义及互相之间的关系）高斯分布的分布概率反解
1.正态分布
参考博客：https://www.cnblogs.com/htj10/p/8621771.html
概率密度函数的意义：理解概率密度函数 - 知乎 (zhihu.com)
若随机变量 
服从一个位置参数为
、尺度参数为
的概率分布，且其概率密度函数为:
：是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与邻近的值的概率大，而取离越远的值的概率越小。正态分布以
为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于。
位置（形状）参数控制分布函数形状的变化。
：是正态分布的尺度参数，描述正态分布资料数据分布的离散程度，越大，数据分布越分散，越小，数据分布越集中。也称为是正态分布的形状参数，越大，曲线越扁平，反之，越小，曲线越瘦高。
尺度参数控制分布函数在幅度上的变化。
则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作
。
随机变量：随机变量可以看做是关联了概率值的变量，即变量取每个值有一定的概率。
随机变量取每个具体的值的概率为0，但在落在每一点处的概率是有相对大小的，描述这个概念的，就是概率密度函数。
一般正态分布
当
,
时，称为标准正态分布。
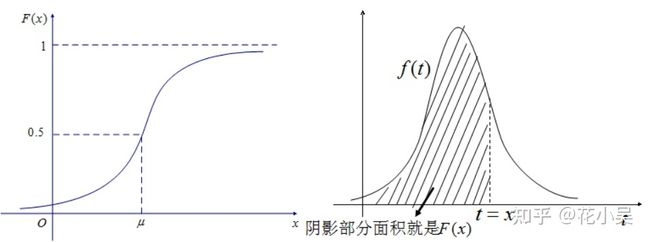
2.正态分布的分布函数
一般正态分布的分布函数
:
标准正态分布的分布函数
:
设，则
分布函数的意义：随机变量的概率，分布函数就是变量小于等于某个特定值a的概率
补充：随机变量的引入，使我们能用实数来描述各种随机现象的结果，但随机变量和普通函数之间还是有着本质的区别，不能运用我们已有的手段处理它；
而分布函数是一个普通函数，正是通过它，我们将能利用数学分析的方法对随机试验的结果进行深入广泛的研究；
实际应用是要和理论接轨的，所以理论上是用分布函数来研究的，实际应用也是在用分布函数做，事实证明这样做确实好。
3.Q函数
Q函数又称标准正态分布的右尾函数，又叫（标准正态分布的）互补累计分布函数
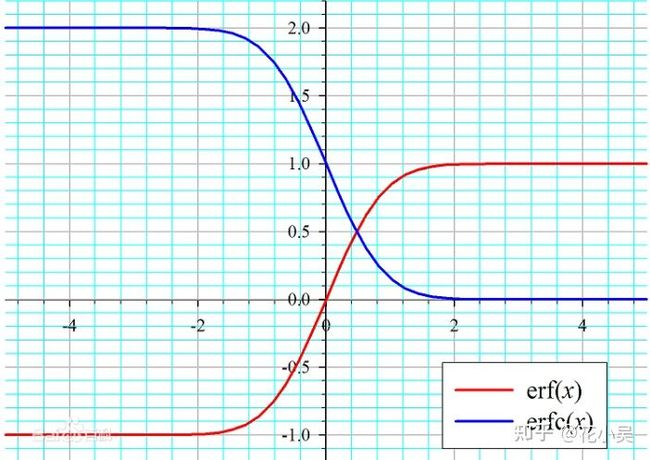
4.误差函数erf(高斯误差函数)
作用：求解高斯分布的概率，已知门限（gate）变量的值，已知变量X>gate的概率。
https://blog.csdn.net/qq_28093585/article/details/78982772
matlab:Y = erf(X) Error function
python:
import math from scipy import special from scipy.special import erf
math.erf(x) special.erf(x) erf(x)5.互补误差函数erfc
作用：求解高斯分布的概率，已知门限（gate）变量的值，已知变量X>gate的概率。
matlab:Y = erfc(X) Complementary errorfunction
python:
import math from scipy import special from scipy.special import erfc
math.erfc(x) special.erfc(x) erfc(x)
6.准确计算比例互补误差函数erfcx（）
由于这个用的较少，有需要理解的可以参考下面博客链接。
准确计算比例互补误差函数erfcx（）
matlab:Y = erfcx(X) Scaled complementary errorfunction
python:
import math from scipy import special from scipy.special import erfc
math.erfcx(x) special.erfcx(x) erfcx(x)6.误差函数的反函数（erfinv）
作用：已知概率，求门限，即求定积分的下限。
高斯分布的分布概率反解：已知X>gate的概率，求解 门值变量gate。
matlab:X = erfinv(Y) Inverse errorfunction
python:
import math from scipy import special from scipy.special import erfc
math.erfinv(x) special.erfinv(x) erfinv(x)7.互补误差函数的反函数（erfcinv）
作用：已知概率，求门限，即求定积分的下限
高斯分布的分布概率反解：已知X>gate的概率，求解 门值变量gate。
具体的求解过程参考下篇文章，写好之后会附上链接。
matlab：X = erfcinv(Y) Inverse complementary errorfunction
python:
import math from scipy import special from scipy.special import erfc
math.erfcinv(x) special.erfcinv(x) erfcinv(x)8.Q函数、误差函数，互补误差函数之间的关系
通过虚警概率求得检测门限的具体过程参考下面文章：
注意：
由正态分布密度函数的总积分为1（即概率 P(X<∞) = 1）得：
补充：
erfc如何查表求解
erf、erfc公式及其函数值表查询_fighting猿的博客-CSDN博客_erf函数
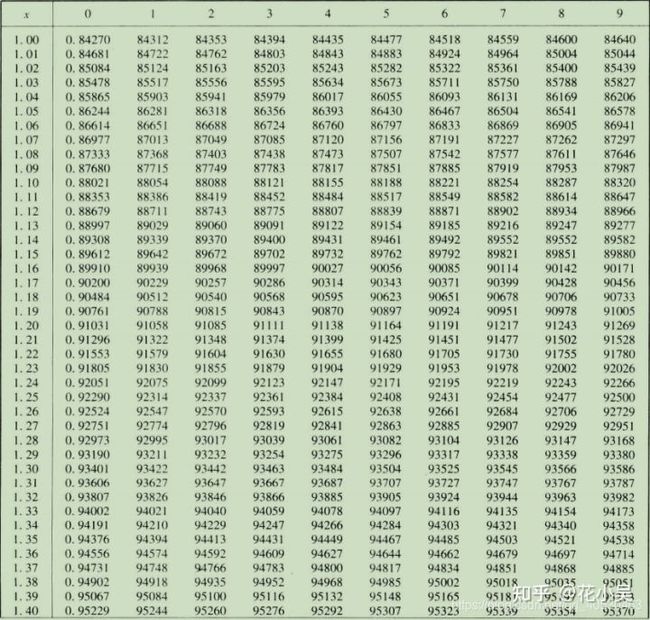
先看左上角的x，纵轴到百分位，横轴对应该百分位值后的千分位值。
实例：
x=1.000时，erf(1.000)=0.84270
x=1.001时，erf(1.001)=0.84312
x=1.002时，erf(1.002)=0.84353
当你想要查erfc的函数值时，如果表中有该函数，直接跟erf一样查询即可，如果没有的话，可根据相同x，erf和erfc的函数值之和为1求出。
x=1.001，erfc(1.001)=?
erf(1.001)+erfc(1.001)=1 查表知 erf(1.001)=0.84312
erfc(1.001)=1-0.84312=0.15688