基于典型相关性分析(CCA)的多视图学习方法综述
本文主要借鉴自《Canonical Correlation Analysis (CCA) Based Multi-View Learning: An Overview》,转载自伍冬睿科学网博客,链接地址:https://blog.sciencenet.cn/blog-3418535-1195519.html
1 多视图学习与典型相关性分析
多视图学习是将两个或两个以上的视图数据加以融合的机器学习策略。在实际生活中,很多数据都可以从多个“视角”进行描述,例如同一个物体从不同角度拍摄的图片,同一个语义的不同语言的表达,或者是同一个网页上包含的文字和链接等。这些来自不同视角的表示数据都可以当作是不同的视图。除了同时利用多个视图特征带来的信息量的增加以外,多视图学习在本质上更注重挖掘数据之间的差异性和互补性,在已有数据的基础上,从算法层面优化学习的效果。
多视图学习方法主要分为以下三类:
- 协同训练(Co-training): 首先对已经标注的数据按一定的规则进行划分,从划分后的数据中训练两个不同的分类器,并分别对未标注的数据进行预测;然后将两个分类器输出的置信度较高的样本作为已经标记的样本加入对方的训练样本池中。采用这种方式交替地训练模型,直到所有未标记的样本都被标记。
- 多核学习(Multi-kernel learning):这种方法是指将不同视图的数据采用不同的核函数映射到不同的特征空间,然后采用线性或者非线性的方法对映射到不同空间的特征进行融合。
- 子空间学习(Subspace learning):子空间学习假设不同视图的数据都可以由一个共享隐空间生成。在这个共享隐空间中可以更好地利用不同视图的数据。
本文介绍的基于典型相关性分析(Canonical Correlation Analysis,CCA)的多视图学习方法是子空间学习中的一类重要方法。典型相关性分析最早由H. Hotelling在1936年提出,它的主要思想是通过最大化两个视图之间的相关系数,寻找各个视图到共同空间的映射向量(典型向量), 在这个共同空间中,各个视图具有最大相关性。
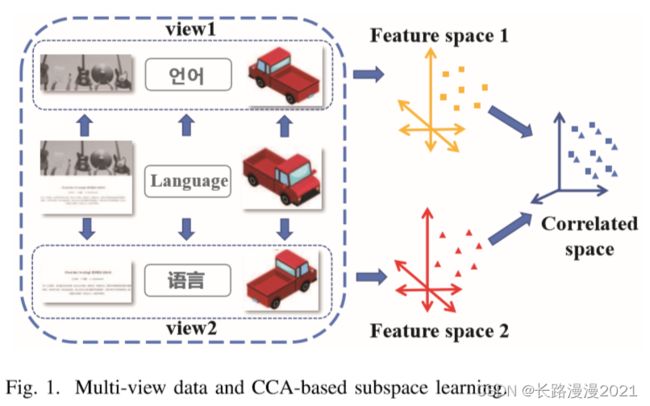
传统的CCA具有以下三点局限性:
- 它不能计算三个或三个以上视图的相关性;
- 它只能计算视图之间的线性相关性。在实际的应用中,视图之间可能是非线性相关的关系。
- 传统的CCA是一种无监督的方法,忽略了标签的信息。在有监督的问题中,充分利用标签的信息能够帮助我们提取到更具判别性的特征。
2 基于CCA的多视图学习方法总结
为了克服传统CCA的不足,许多基于CCA的扩展方法被提出,接下来将针对以上三点局限性分别进行介绍。
2.1 广义典型相关性分析 (Generalized CCA)
针对CCA只能处理两个视图数据的问题,为了最大化多个视图的相关性,主要的解决方法有直接法和间接法:
- 间接法:这种方法非常容易理解,对于具有多个视图的数据,首先成对地计算视图之间相关系数,然后最大化所有相关系数的和。
- 直接法:通过对多个视图的高维协方差矩阵进行分析,直接最大化所有视图的相关性。
下表简单地总结了经典的广义CCA方法:
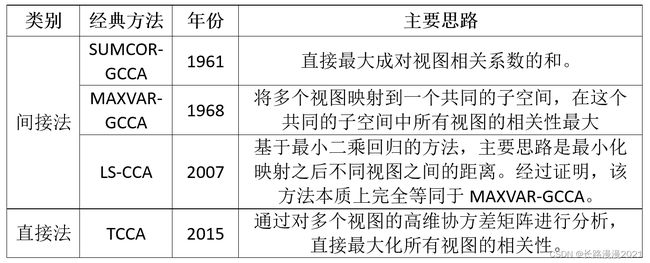
2.2 非线性典型相关性分析 (Nonlinear CCA)
针对传统CCA不能计算数据之间的非线性相关性的问题,有三种主要的解决思路:
- 核映射:首先利用核函数将数据映射到高维的空间中,然后应用线性CCA对相关性进行计算。最具有代表性的方法是核典型相关性分析(Kernel Canonical Correlation Analysis, KCCA)。这类方法的计算复杂度高,容易过拟合,要选择一个合适的核函数也相对来说比较困难。 为了降低KCCA的计算复杂度,除了使用核函数以外,也可以通过对数据进行随机非线性映射实现同样的目的,如Randomized Nonlinear Canonical Correlation Analysis (RCCA)。
- 局部保留:基于局部保留的思路来源于图模型,旨在实现全局非线性降维的同时保留数据局部的线性结构,例如Locality preserving CCA (LPCCA)。该方法的缺点在于需要计算近邻,当样本数量巨大的时候,计算量大。
- 神经网络:基于神经网络的方法可以处理非常复杂的数据之间的非线性关系。做法是首先利用神经网络对数据进行非线性映射,然后利用线性CCA计算数据映射之后的相关性。Andrew在2013年首次提出了基于深度神经网络的CCA (Deep Canonical Correlation Analysis, DCCA)获得了广泛的关注; 然后Weiran Wang进一步结合自编码器提出了DCCAE (Deep Canonically Correlated Auto-Encoders); Bach将变分自编码器的思想融合CCA, 提出变分CCA (Variational Canonical Correlation Analysis, VCCA)。这类方法的缺点在于模型参数多,对数据量的要求比较高。
2.3 有监督典型相关性分析(Supervised CCA)
类别信息对于有监督的学习来说非常关键。为了充分利用标签信息,最常见的思路是将CCA与线性判别分析(Linear Discriminant Analysis, LDA)结合,在最小化视图类内相似度的同时最大化类间相似度。代表性的方法有判别式CCA (Discriminative CCA, DisCCA),MLDA (Multi-view Linear Discriminant Analysis)和MULDA (Multi-view Uncorrelated Linear Discriminant Analysis)。除此之外,也可以将标签的独热编码矩阵作为其中一个视图,直接使特征和标签相关,代表性的方法是DGCCA (Deep Generalized CCA)。
下表简要对比了各种基于CCA的多视图学习方法的区别,各个方法的具体介绍请参见原文:

3 应用
基于CCA的多视图学习方法具有广泛的应用,主要包括以下四个方面:
3.1 多视图模式识别
多视图模式识别主要包括多视图分类和多视图回归。应用领域包括广告分类,文本分类,以及计算机视觉中的手写字体识别、姿态识别、人脸识别等。
CCA在其中发挥的作用主要是为各个视图分别学习一种新的特征表示。那么应该如何利用新学习到的多个视图的特征呢?关于这个问题,各个文章中的方法不尽相同,主要包含以下三种方法:
- 直接将新学习到的各个视图的特征拼接起来送入分类器;
- 计算典型向量的时候使用两个视图,在训练分类器和预测的时候只使用一个视图映射之后的特征;
- 在计算典型向量的时候将标签作为一个视图,预测时直接在特征视图中利用近邻分析得到预测结果。
3.2 跨模态检索与分类
这里的“模态”可以简单地理解为前面说的“视图”。随着网上多媒体数据的快速增长,跨模态检索是一个重要的研究领域。以图片和文本为例,跨模态检索是当指输入查询文本时能检索到与之相关的图片,例如我们使用文本“猫”来检索猫的相关图片,反之亦然。 跨模态检索的难点在于需要克服不同模态之间的“语义鸿沟”,因为来自不同模态的数据是不完全一致的,我们很难对他们进行有效的距离度量。CCA可以将不同模态的数据映射到一个共同的相关空间,在这个空间中就可以对不同模态的数据进行有效的距离度量,从而完成跨模态检索的任务。
跨模态分类是指在一个模态上训练分类器,而在另一个模态上进行分类预测。使用CCA对两个模态进行相关性映射,映射之后的对应样本可以认为在共同空间中距离非常近,此时在一个模态上训练的分类器,也就可以对另外一个模态的样本进行预测。
3.3 多视图嵌入
CCA的另外一个重要应用就是自然语言处理中的词嵌入,即为多种语言的词向量学习到具有更好的相似性度量的表示。除此之外,学习到的特征表示的维度也能大大降低,这非常有利于后续的其它处理。
3.4 脑机接口
CCA在脑机接口中的主要应用是稳态视觉诱发电位(Steady-State Visual Evoked Potentials, SSVEP)的频率识别。SSVEP作为脑机接口的三大范式之一,在字符输入方面表现优异。其主要原理是当人眼接收到固定频率的刺激时,会产生与刺激频率相关的脑电信号。CCA在SSVEP中最简单的应用方法就是直接计算所采集的脑电信号与人工构造的特定频率的模板信号之间的相关性,根据相关性的大小给出频率识别的结果。
4 小结
本文对基于CCA的多视图学习方法进行了总结和对比,并且介绍了这些方法在模式识别、跨模态检索与分类、多视图嵌入以及脑机接口中的应用。
本工作由华中科技大学人工智能与自动化学院硕士生郭陈凤和伍冬睿教授共同完成。
全文请见:C. Guo and D. Wu, “Canonical Correlation Analysis (CCA) Based Multi-View Learning: An Overview,” Neural Computing and Applications, 2019, submitted.
arXiv版本:https://arxiv.org/abs/1907.01693
中文版本:基于典型相关分析的多视图学习方法综述