机器人学导论第二章

机器人学导论第二章

我们定义的位姿都是通过世界坐标系定义的笛卡尔坐标系。

点的位置可以用矢量描述；物体的姿态可以用固定在物体上的坐标系来描述，用一个矩阵来表示。
…Page 21 - 22
旋转矩阵的逆矩阵等于它的转置。旋转矩阵是单位阵。

位置和姿态经常成对出现，因此将其称作坐标系，四个矢量为一组，表示了位置和姿态的信息。一个矢量指向位置，另外三个矢量表示姿态，等价于一个坐标系可以用一个位置矢量和一个旋转矩阵描述。如果位置矢量是零矢量，那它表示的就是姿态。

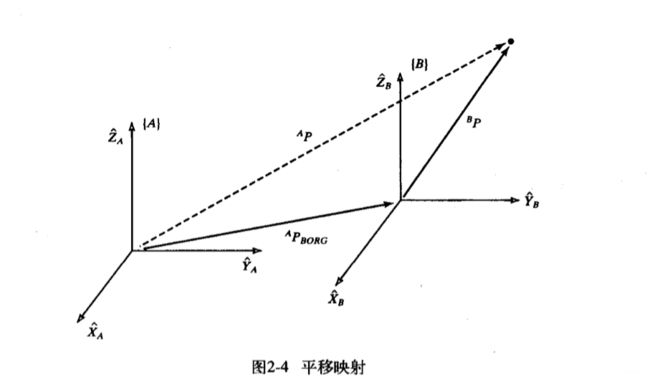
2.3映射：从坐标到坐标轴的变换。
不同坐标系中的矢量只有在坐标系的姿态相同这种情况下才可以相加。
平移坐标系的映射:（在姿态相同的情况下才可以平移）
（1）

旋转坐标系的映射：
旋转矩阵：坐标系B对于坐标系A的三个单位方向向量作为列向量组成的3x3矩阵

问题根据题目写出坐标系B的旋转矩阵：矩阵的由三个单位列向量组成，且第一个向量是B坐标系x轴相对于A坐标系的 单位 向量。

对于一般情况，我们将求一个中间坐标系T使其和姿态坐标系A相同，原点和坐标系B相同，再运用以上关系求出映射。
（2）
由上似引出新的形式：
（3）
即用矩阵形式的算子表示了一个坐标系到另一个坐标系的映射。
为了用（3）的矩阵算子的形式写出（2）式，定义一个4x4的矩阵算子并使用了4x1位置矢量，这样（3）就变成了：
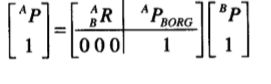（4）
其中 等式中4x4的矩阵为齐次变换矩阵。

2.4 算子： 平移、旋转和变换

• 用于坐标系间点的映射的通用数学表达式称为算子，包括点的平移算子、矢量旋转算子和平移加旋转算子。

平移算子：

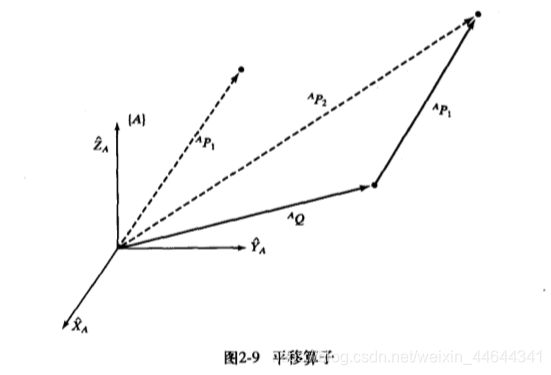
（AP1沿AQ矢量方向移动，得到一个新的矢量）
(1)
用矩阵算子写出：
（2）
其中：

矢量q为平移矢量AQ。矢量AQ的方向决定了AP1的移动方向，决定式子中的符号变化。

旋转算子:同2.3

旋转算子R表示绕k轴旋转theta角度。
注意是向前旋转还是向后旋转，反向若不同需用旋转算子的逆。

2.5 总结

• 一个4x4的齐次变换阵包含旋转与位置信息，相当于一个是矢量旋转和平移的变换算子。
• 齐次变换阵是坐标系的描述、是变换的映射、是变换算子。

2.6 变换算法
混合变换:

逆变换：

2.7 变换方程
若已知以下两个坐标系相对关系


可得出：

若只有一个未知量，则可通过其它变换求出：

2.8 姿势的其它描述方法
旋转矩阵也可被称为标准正交矩阵，行列式为+1（非标准为-1）

用少于9个数字来表示一个姿态（正交矩阵的凯莱公式）
X-Y-Z固定角坐标系：首先将坐标系{B}和一个已知参考坐标系{A}重合。先将{B}绕X轴旋转γ角，再绕Y轴旋转β角，最后绕Z轴旋转α角。每个旋转都是绕着固定参考坐标系{A}的轴。我们规定这种姿势的表示法为X-Y-Z固定角坐标系。有时把它们定义为回转角、俯仰角和偏转角。
可直接推导出等价的旋转矩阵

（1）
其中cα为cosα的简写，以此类推。最重要的是搞清楚（1）式中的旋转顺序。
由（1）可推出结果：
（2）

逆解问题：根据旋转矩阵求出等价X-Y-Z固定角坐标系

要求出对应固定角坐标系需要三个方程三个变量：

虽然存在第二个解，但在上式中取β的正根以得到单解，满足**-90°≤β≤90°**。这样就可以在各种姿态表示法之间定义一一对应的的映射函数。

Z-Y-X欧拉角：首先将坐标系{B}和一个已知参考坐标系{A}重合。先将{B}绕Z轴旋转α角，再绕Y轴旋转β角，最后绕X轴旋转γ角。**在这种表示方法中，每次都是绕运动参考系{B}的各轴旋转而不是绕固定坐标系{A}的各轴旋转。**这样三个一组的旋转被称为欧拉角。

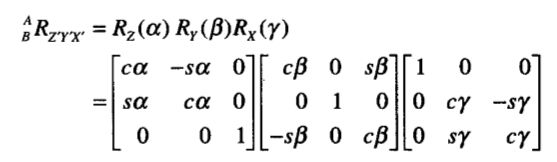
计算结果与以相反顺序绕固定轴旋转三次得到的结果完全相同。
三次绕固定轴的最终姿态和以相反顺序三次绕运动坐标轴旋转的最终姿态相同。

Z-Y-Z欧拉角：首先将坐标系{B}和一个已知参考坐标系{A}重合。先将{B}绕Z轴{B}旋转α角，再绕Y轴旋转β角，最后绕Z轴旋转γ角。

如果sinβ ≠ 90°可得到：

虽然存在第二个解，但我们总是满足0.0≤β≤180.0°的单解。
如果β=0.0，则解为：

如果β=180.0°，则解为；

其它坐标系表示方法:见附录B（24种）