图深度学习——卷积神经网络&循环神经网络&自编码器
卷积神经网络
常用做图像分类任务。举例：识别图中的兔子
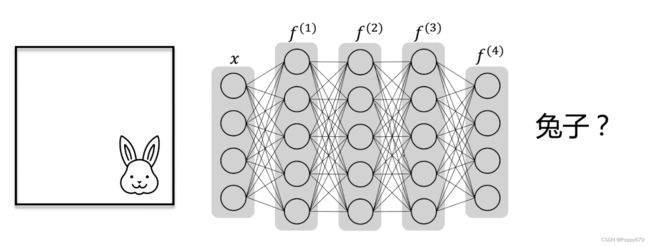
前馈神经网络做兔子图像识别
图像可以通过矩阵表示，然后将矩阵转换成向量，就可以作为前馈神经网络的输入，但是
1.参数量就非常大，需要大量数据进行训练，不然模型泛化能力会不够好。
2.图像中兔子的位置改变后，前馈神经网络就无法处理，因为当兔子在图像中的位置改变后，图像矩阵转换成向量的值也会不同，那么就需要模型去学习很多数据。
因此前馈神经网络并不能很好的处理这样的图像分类问题，兔子位置改变，同样都是兔子的图像数据经过前馈神经网络后可能出现不相同的输出，即不能很好的捕捉兔子的信息进行分类。
卷积神经网络就解决了上述问题。
卷积
稀疏连接
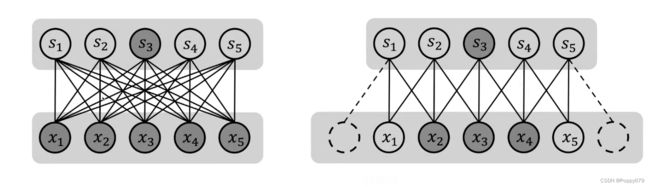
左边：全连接，右边：卷积
S 3 S_3 S3 在全连接中，与所有的神经元相关； S 3 S_3 S3 在卷积中，只与周围邻接神经元相关，而不是和所有神经元相关。由此可知，稀疏连接的作用是让网络的输出仅仅关注与之相邻的神经元，而不是关注整个神经元。
参数共享
同一批参数参与一次计算——卷积核
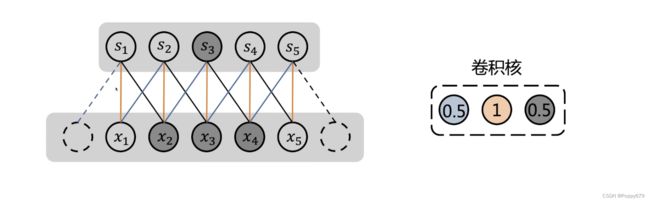
卷积操作
滑动卷积核来进行卷积操作。通常不止是用一个卷积核，而是使用多个卷积核（不同卷积核中参数是不一样的）如下图所示，是一维卷积操作。
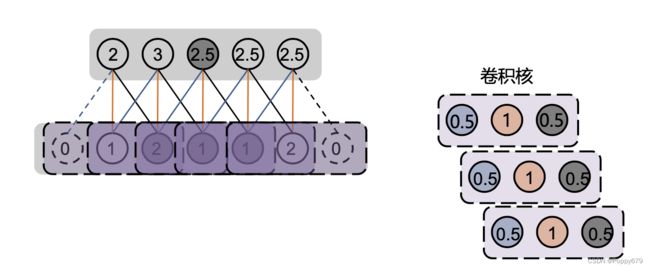
二维卷积也是类似的滑动操作。
平移等变
参数共享带来好处——平移等变，输入滑动一格，输出也会同等滑动一格。通过这样的平移等变的特点，捕捉到的信息都是一样的，只是位置是不同的，这样就大大的增加了表达性，提高了模型的泛化能力。
卷积操作性质
- 稀疏连接
- 参数共享
- 平移等变
前两点性质使得卷积神经网络相对于前馈神经网络有更好的可拓展性（Scalability）。三个性质使得卷积神经网络有更好的泛化能力（ Generalization）。
池化
池化能够扩大模型的感受野，即每个输出对应的输入的区域能够更大
最大池化：求感受野中的最大值
平均池化：求感受野中所有值的平均
卷积神经网络整体框架
如图所示是二维的卷积神经网络。卷积再池化其实是一个特征提取的过程，最后对数据转换为向量通过一层神经网络来进行分类输出。
循环神经网络
RNN处理序列数据：文字、时序（股票等）
序列数据上的任务
机器翻译：输入是一个序列，输出也是一个序列
语义分析：输入是一个序列，输出可能只是一个元素（好/坏）
可以用前馈神经网络来处理序列数据嘛？
不可以。
1.因为序列可能长短不一，那么前馈神经网络就不好处理了；如果想要使用前馈神经网络需要对序列长度进行统一，固定。
2.序列数据中同一信息可能出现在序列的不同位置，那么前馈神经网络无法处理这样的问题，无法输出相同的信息。
循环神经网络
循环神经网络中有两个输入，一个是 h 0 h_0 h0：初始化信息或来自上一步的信息；一个是输入 x 1 x_1 x1，通过网络将两个输入都整合起来。
其中通过前馈神经网络来建模， h i h_i hi 作为当前步积累的信息传到下一步中， y i y_i yi 是当前步的输出（有需要的话），因此RNN也存在一定灵活性。在RNN中，参数也是共享的。
序列增长，就增加对相应 x x x 的计算，这样就解决了序列长度不一的问题。因为参数事共享的，那么不同位置的相同信息能够被捕捉到。
RNN的性质
- 处理不同长度的序列
- 捕捉序列的顺序信息
- 参数共享
RNN梯度消失和梯度爆炸
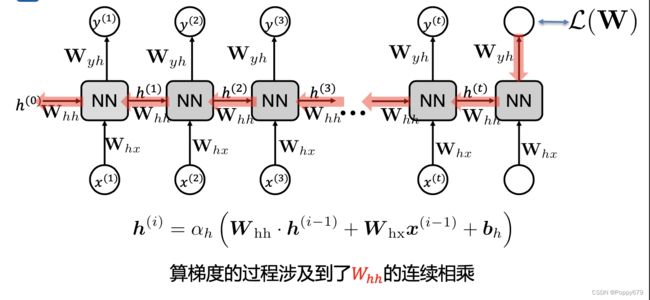
当关注最后一个输出时，可以发现计算这个输出的权重是需要不断往前计算。在计算梯度的过程中，会涉及到 W h h W_hh Whh 的连续相乘。比如，当一些小于1的权重连续相乘时，结果就会越来越小，趋近于0，这样以来梯度就消失了。因此，RNN无法捕捉到很长距离的信息。
Last summer, I went to Yellowstone Natiinal Park. I went to Yellowstone National Park last summer.
比如这里的last summer可能就会因为距离过长而导致无法捕捉信息，导致对后面的计算影响不大。
那么当一些大于1的权重连续相乘时，结果就会越来越大，就会出现梯度爆炸。
LSTM 长短时记忆网络
为了缓解RNN中梯度问题，提出了改进的RNN模型——LSTM。整体结构是和RNN类似的，但是神经网络部分使用LSTM模块取代。
LSTM神经单元
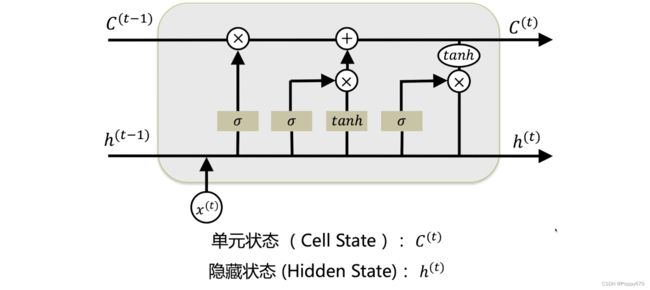
在LSTM神经单元中，相比RNN增加了1个状态值，就是单元状态（Cell State）。 h t h_t ht 相当于RNN中的 y t y_t yt，需要时可以直接输出，不需要也存在。
红色高亮部分就是LSTM单元中的门（gate，运算）.
遗忘门：在LSTM中，之前序列的信息是保留在 C t C_t Ct 中。遗忘门控制哪些历史信息可以通过网络。遗忘门也是通过前馈神经网络来进行建模的。 W f W_f Wf， U f U_f Uf 都是参数， b f b_f bf 是偏差。
输入门：控制哪些新的信息可以进入网络。
候选值：更新 C t C_t Ct 时，要从输入信息中选一些信息来更新。 C t C_t Ct 候选值计算公式如下：
新的单元状态–更新 C t C_t Ct：通过遗忘门来判断保留哪些信息，然后结合上面计算得到的候选值来更新单元状态 C t C_t Ct
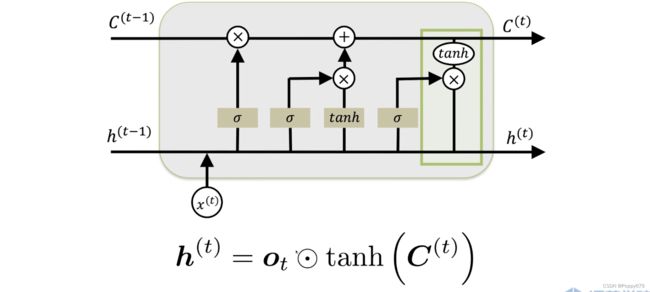
输出门：建模方式和输入门，遗忘门相同，参数不同。输出门用来生成 h t h_t ht。 h t h_t ht在很多时候会作为输出。LSTM的输出就是对单元状态和包含之前序列信息的结合。
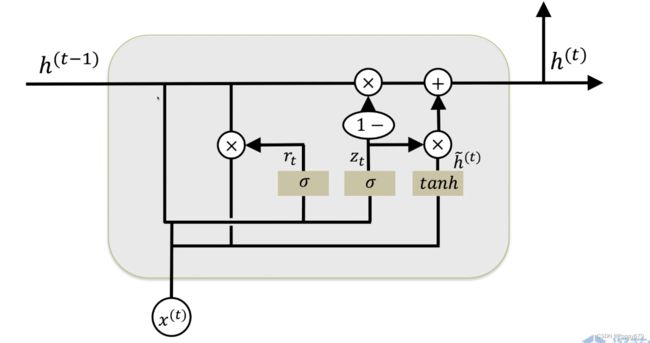
GRU
对LSTM进行了一些优化，把一些门合并。
自编码器
现实世界中，大多数数据是没有ground truth，因此要采用无监督学习。之前介绍的有监督学习需要大量的ground truth。
一个自编码器由编码器，隐藏层和解码器组层。编码器和解码器都可以用神经网络建模。可以不止一层，也可以是其他网络来进行建模（CNN， RNN等）
自编码器的目标是使得 h h h 能很好的编码 x x x 中的信息， x ^ \hat{x} x^ 是从 h h h 中重建出来的信息，希望 x x x 和 x ^ \hat{x} x^ 尽量的接近，因此构造损失函数（举例）：
ℓ ( x , x ^ ) = ∥ x − x ^ ∥ 2 2 \ell(\mathbf{x}, \hat{\mathbf{x}})=\|\mathbf{x}-\hat{\mathbf{x}}\|_{2}^{2} ℓ(x,x^)=∥x−x^∥22
x x x 和 x ^ \hat{x} x^ 之间越接近，说明 h h h 保留 x x x 中的信息保留的越好。
自编码器中编码器和解码器都可以用更复杂的结构进行替代建模。
自编码器中需要注意的问题：神经网络的表达能力太强的话，也不一定是好事。因为目标是为了使 h h h 尽可能保留 x x x 的信息，但又不希望 x x x 和 x ^ \hat{x} x^ 完全一样，所以通常在 h h h 上加一个“信息瓶颈”，过滤掉不那么重要的信息，保留重要信息。
比如，常见的限制有降低 h h h 的维度，使 h h h 的维度小于输入的维度（欠完备的自编码器）；对 h h h 加上一个正则化项，限制2范数大小（正则化的自编码器）.