数据挖掘-分类
三、数据挖掘-分类
分类是一种很重要的数据挖掘技术,也是数据挖掘研究的重点和热点之一。分类的目的是分析输入数据,通过训练集中的数据表现出来的特性,为每一个类找到一种准确描述或者模型,这种描述常常用谓词来表示。由此生成的类描述用来对未来的测试数据进行分类。尽管这些未来测试数据的类标签是未知的,仍可以由此预测这些新数据所属的类。也可以由此对数据中每一个类有更好的理解。
3.1.1 分类的基本概念
分类(Classification)是一种重要的数据分析形式,它提取刻画重要数据类的模型。这种模型称为分类器,预测分类的(离散的、无序的)类标号。这些类别可以用离散值表示,其中值之间的次序没有意义。
分类也可定义为:
分类的任务就是通过学习得到一个目标函数(Target Function)ƒ ,把每个属性集x映射到一个预先定义的类标号y 。
3.1.2 分类的过程
数据分类过程有两阶段:
(1)学习阶段(构建分类模型)。
(2)分类阶段(使用模型预测给定数据的类标号)。
3.1.3 分类器性能的评估方法
分类器的性能和所选择的训练集和测试集有着直接关系。一般情况下,先用一部分数据建立模型,然后再用剩下的数据来测试和验证这个得到的模型。如果使用相同的训练集和测试集,那么模型的准确度就很难使人信服。保持法和交叉验证是两种基于给定数据随机选样划分的,是常用的评估分类方法准确率的技术。
3.2.1 决策树概述
决策树是数据挖掘的有力工具之一,决策树学习算法是从一组样本数据集(一个样本数据也可以称为实例)为基础的一种归纳学习算法,它着眼于从一组无次序、无规则的样本数据(概念)中推理出决策树表示形式的分类规则。
决策树(Decision Tree)是一种类似于流程图的树结构,其中每个内部节点(非树叶节点)表示在属性上的测试,每个分支表示该测试上的一个输出,而每个树叶节点存放一个类标号,树的最顶层节点是根节点。决策树生成方式一般情况下都是由上而下的。每次不同的事件或决策都有可能引发至少两个以上的事件,形成不同的结果,这种决策方法用图形表示出来很像一棵树,所以称之为决策树。决策树是一种简单且广泛使用的分类器。通过训练数据来构建决策树,可高效地对未知的数据进行分类。
3.2.2 决策树的用途和特性
基于决策树的决策算法是属于实用性很好的总结预测算法之一,是一个趋近于非连续型函数值的算法。决策树在各行各业有着非常多的广泛应用,如在医院的临床决策、人脸检测、故障诊断、故障预警、医疗数据挖掘、案例分析、分类预测的软件系统等方面都有很大的用处。
3.2.3 决策树工作原理
决策树是通过一系列规则对数据进行分类的过程。它提供一种在什么条件下会得到什么值的类似规则的方法。决策树分为分类树和回归树两种,分类树对离散变量做决策树,回归树对连续变量做决策树。
直观看,决策树分类器就像判断模块和终止块组成的流程图,终止块表示分类结果(也就是树的叶子)。判断模块表示对一个特征取值的判断(该特征有几个值,判断模块就有几个分支)。
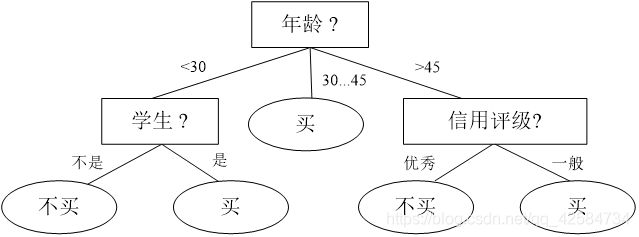
3.2.4 决策树构建步骤
决策树分类算法应用的完整流程应包含建树和应用。建树是从经验数据中获取知识,进行机器学习,建立模型或者构造分类器,是决策树算法的工作重点,通常又将其分为建树和剪枝两个部分。
决策树构建的基本步骤如下:
1.开始,所有记录看作一个节点。
2.遍历每个变量的每一种分割方式,找到最好的分割点。
3.分割成多个节点N1,N2,…,Nm(m的数量与当前的属性相关)。
4.对N1,N2,…,Nm分别继续执行2~3步,直到每个节点足够“纯”为止。(“纯”的含义是要么全部是“是”,要么全部是“否”)。
树的主体建好后,接下来便是对其剪枝。
决策树的剪枝一般通过极小化决策树整体的损失函数或代价函数来实现。
决策树剪枝常用的方法有两种:预剪枝和后剪枝。
预剪枝是根据一些原则尽早停止树的增长,如树的深度达到用户所要的深度、节点中样本个数少于用户指定个数等。预剪枝在建立树的过程中决定是否需要继续划分或分裂训练样本来实现提前停止树的构造,一旦决定停止分枝,就将当前节点标记为叶节点。
后剪枝是通过在完全生长的树上剪去分枝实现的,通过删除节点的分支来剪去树节点。
3.2.5 决策树算法原理
1.认识决策树
1)决策树的生成过程
一棵决策树的生成过程主要分为以下3个部分:
(1)特征选择:特征选择是指从训练数据众多的特征中选择一个特征作为当前节点的分裂标准,如何选择特征有着很多不同量化评估标准,从而衍生出不同的决策树算法。
(2)决策树生成:根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则决策树停止生长。
(3)剪枝:决策树容易过拟合,一般都需要剪枝,缩小树结构规模、缓解过拟合。
基于信息论的决策树算法有ID3、CART和C4.5等算法,其中C4.5和CART两种算法从ID3算法中衍生而来。
CART和C4.5支持数据特征为连续分布时的处理,主要通过使用二元切分来处理连续型变量,即求一个特定的值——分裂值:特征值大于分裂值就走左子树,或者就走右子树。
ID3算法建立在“奥卡姆剃刀”的基础上,越是小型的决策树越优于大的决策树。ID3算法中根据信息论的信息增益评估和选择特征,每次选择信息增益最大的特征来做判断模块。
C4.5是ID3的一个改进算法,继承了ID3算法的优点。C4.5算法用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多的属性的不足,在树构造过程中进行剪枝;能够完成对连续属性的离散化处理;能够对不完整数据进行处理。
CART算法采用的是基尼(Gini)指数(选Gini指数最小的特征s)作为分裂标准,同时它也是包含后剪枝操作。
3.3.1 贝叶斯定理
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理(Bayes theorem)为基础,采用了概率推理方法。
条件概率:表示事件B已经发生的前提下,事件A发生的概率,称为事件B发生下事件A的条件概率。其基本求解公式为:
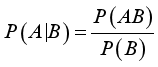
贝叶斯定理之所以有用,是因为在生活中经常遇到这种情况:可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但人们往往更关心P(B|A),贝叶斯定理打通了从P(A|B)获得P(B|A)的道路。
贝叶斯定理:

3.3.2 朴素贝叶斯分类原理与流程
朴素贝叶斯分类是贝叶斯分类的一种,朴素贝叶斯分类与贝叶斯分类相比,后者需要花很大的时间和空间复杂度去计算类条件概率。
1. 朴素贝叶斯分类原理
朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。
朴素贝叶斯分类的正式定义如下:
(1)设x={a1,a2,…,am},为一个待分类项,而每个a为x的一个特征属性。
(2)有类别集合C={y1,y2,…,yn}。
(3)计算P(y1|x),P(y2|x),…,P(yn|x)。
(4)如果P(yk|x)=max{P(y1|x),P(y2|x),…,P(yn|x)},则xϵyk。
2.朴素贝叶斯分类流程
整个朴素贝叶斯分类可分为三个阶段:
第一阶段是准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类,形成训练样本集合。
第二阶段是分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计,并将结果进行记录。
第三阶段是应用阶段。
这个阶段的任务是使用分类器对分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。
3.3.3 贝叶斯分析
贝叶斯分析中的三要素(即贝叶斯统计三要素,一要素是先验概率P(A),二要素是条件概率P(A|B),最终得到三要素即后验概率P(B|A)。
理解贝叶斯分析最好的方法即图像法,如图所示。A为红圈,B为蓝圈,AB为紫圈。这里的A(红圈的面积即先验,后验是阴影占蓝圈(B)的百分比。

3.3.4 贝叶斯决策
贝叶斯决策主要包含四个部分:数据(D)、假设(W)、目标(O)和决策(S)。
贝叶斯决策步骤:
1.理清因果链条,确定哪个是假设,哪个是证据。
2.给出所有可能假设,即假设空。
3.假设,即假设空间。
4.根据贝叶斯概率公式求解后验概率,得到假设空间的后验概率分布。
5.利用后验概率求解条件期望,得到条件期望最大值对应的行为。
贝叶斯决策如果一旦变成自动化的计算机算法,它就是机器学习。用贝叶斯决策诠释一个最简单的机器学习分类算法,那就是朴素贝叶斯。
3.4.1 支持向量机主要思想
支持向量机(SVM)是根据统计学习理论中的结构风险最小化原则提出的一种经典的机器学习方法,现已发展为机器学习领域的一个重要分支。
SVM主要思想是针对两类分类问题的,寻找一个超平面作为两类训练样本点的分割,以保证最小的分类错误率。在线性可分的情况下,存在一个或多个超平面使得训练样本完全分开,SVM的目标是找到其中的最优超平面,最优超平面是使得每一类数据与超平面距离最近的向量与超平面之间的距离最大的平面;对于线性不可分的情况,可使用非线性核函数将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分。
3.4.2 支持向量机基础理论
支持向量机的理论有三个要点,即:
(1)最大化间隔。
(2)核函数。
(3)对偶理论。
1. 最大化间隔
在样本线性可分的情况下,可行的分类超平面可能会有很多,如下图中的L1、L2和L3。
从图中可以直观看出,L2比另外两条分界线要更好,这是因为L2离样本的距离更远一些,让人觉得确信度更高。
SVM正是基于这种直观思路来确定最佳分类超平面的:通过选取能够最大化类间间隔的超平面,得到一个具有高确信度和泛化能力的分类器,即最大间隔分类器。
2. 核函数
核函数的定义:
设s是输入空间(欧氏空间或离散集合),H为特征空间(希尔伯特空间),如果存在一个从s到H的映射 ![]() 使得对所有的x,zϵs,函数
使得对所有的x,zϵs,函数 ![]() ,则称K(x,z),为核函数。
,则称K(x,z),为核函数。 ![]() 为映射函数,
为映射函数, ![]() 为x,z映射到特征空间上的内积。
为x,z映射到特征空间上的内积。
常用的核函数主要有以下几种:
(1)线性核函数(Liner)。
(2)多项式核函数(Polynomial)。
(3)高斯(Gaussian)核函数(又称径向基函数,RBF)。
(4)指数型径向基核函数。
(5)Sigmoid(或2层感知机)。
(6)傅立叶(Fourier)核函数。
-
对偶理论(Duality Theory)
1947年由美籍匈牙利数学家冯·诺依曼创立对偶理论。
对偶理论就是研究线性规划中原始问题与对偶问题之间关系的理论。对偶问题有许多重要的特征,它的变量能提供关于原始问题最优解的许多重要资料,有助于原始问题的求解和分析。对偶问题与原始问题之间存在着具体关系,见下表。

原—对偶优化方法:
1)凸优化问题
凸优化问题是线性规划中一种重要的特殊情形,它具有很好的性质。如果凸规划的目标函数是严格凸函数,又存在极小点,那么它的极小点是唯一的,局部极小点就是全局极小点。
2)原—对偶算法
原—对偶算法作为一种解决复杂调度和整数规划问题的有效方法,已经被成功应用于网络调度问题。
应用原—对偶算法的前提条件是待求解优化问题必须是严格的凸优化问题。其核心思想是设计算法通过求解原优化问题的对偶问题,来得到原问题的最优解。 -
几种常用的损失函数
1)lp损失函数
2)ϵ-不灵敏损失函数
3)logistic损失函数 -
结构风险最小化
结构风险最小化思想:首先,把函数集分解为一个函数子集序列,使各个子集能够按照复杂性大小排列,也就是按照VC维大小排列,这样在同一个子集中置信范围就相同;其次,在每个子集中寻找最小经验风险,通常它随着子集复杂度的增加而减少。最后,选择最小经验风险与置信范围之和最小的子集,就可以达到期望风险的最小,这个子集中使经验风险最小的函数就是要求的最优函数。
支持向量机是一种比较好的实现了结构风险最小化思想的方法。
3.4.3 支持向量机原理 -
支持向量机(SVM)
支持向量机(SVM)是一种分类算法,通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。
SVM主要有以下3种情况:
1)线性可分情况。
2)线性不可分情况
线性可分就是在样本存在的空间中,可以找到可能正确划分训练样本的最优分类超平面。但在现实中无法找到一个使得所有训练样本关于分类超平面的间隔都是正值的分类超平面。必须适当软化条件。
对于那些需要软化的条件,将它们分为两类:一类是虽不满足KKT条件但是可以被正确划分的点;另外一类是不满足KKT条件也不能被正确划分的点。
遇到线性不可分时,常用做法是把样例特征映射到高维空间中去,如下图所示。

线性不可分映射到高维空间,可能会导致维度大小高到可怕的程度,导致计算复杂。核函数的价值在于它虽然也是讲特征进行从低维到高维的转换,但核函数事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就避免了直接在高维空间中的复杂计算。
3)非线性可分情况
即便是引入了松弛变量,用直线划分有些问题还是存在很大误差,即输入空间中不存在该问题的线性分类超平面,这种问题叫非线性可分问题。处理这类问题时,通过某种映射使得训练样本线性可分,即将输入空间映射到高维空间中后,通过训练支持向量机得到该问题在高维空间中的最优分类超平面,解决该类分类问题。
2.支持向量机(SVM)的优点
SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法都采用一种基于贪心学习的策略来搜索假设空间,这种方法一般只能获得局部最优解。