ccc-sklearn-7-SVM（1）
1.SVM概述
源于统计学习理论，是强学习器。中文名为支持向量网络，效果十分强大，不管是线性还是非线性分类中都十分有效。是最接近深度学习的机器学习算法。
在手写识别数字和人脸识别中应用广泛，在文本和超文本分类中可以大量减少标准归纳和转换设置中对标记训练实例的需求。同时也常被用于执行图像的分类，并用于图像分割系统。总之就是强啦。。
| 功能 | |
|---|---|
| 有监督学习 | 线性二分类与多分类（Linear Support Vector Classification） 非线性二分类与多分类（Support Vector Classification, SVC） 普通连续型变量的回归（Support Vector Regression） 概率型连续变量的回归（Bayesian SVM） |
| 无监督学习 | 支持向量聚类（Support Vector Clustering，SVC） 异常值检测（One-class SVM） |
| 半监督学习 | 转导支持向量机（Transductive Support Vector Machines，TSVM） |
支持向量机分类器是如何工作的
简单说，就是在下图的分布中找出一个超平面作为决策边界，使模型在数据上的分类误差尽量小，尤其是对于未知数据集上的分类误差（泛化误差）尽量小
超平面是维度小于分布维度的空间。二分类问题中，称能划分数据集的超平面是数据的“决策边界”
对于下图的数据集中，让训练误差为0的决策边界有无数条。
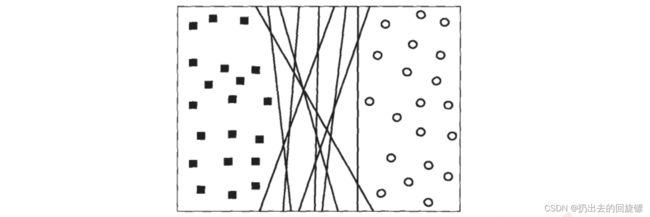
但是不是每一条在未知数据上的表现也会变得优秀。对于任何一条可能的决策边界，让它们向两边平移，直到碰到这条决策边界最近的方块和圆圈后停下，形成两个新的超平面，然后将原始的决策边界移动到这两个超平面中间。新的超平面之间的距离叫做决策边界的边际d
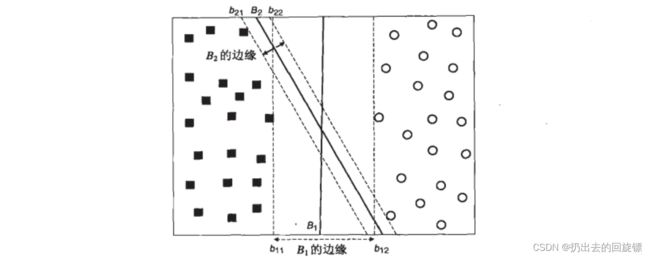
支持向量机，就是通过找出边际最大的决策边界，来对数据进行分类的分类器。可以通过结构风险最小化定律证明（SRM）拥有更大边际的决策边界在分类中的泛化误差更小，边际很小的情况下容易出现’过拟合’现象
sklearn中的支持向量机
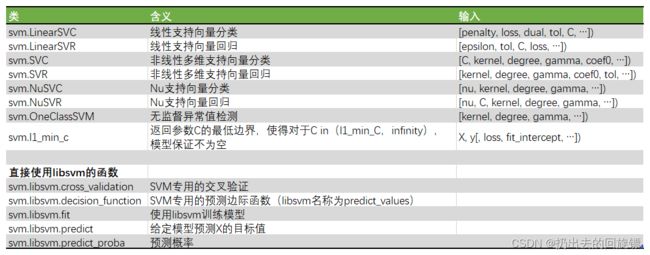
- 除了特别表明是线性的两个类LinearSVC和LinearSVR之外，其他的所有类都是同时支持线性和非线性的
- NuSVC和NuSVC可以手动调节支持向量的数目，其他参数都与最常用的SVC和SVR一致
- 注意OneClassSVM是无监督的类
2.线性SVM用于分类的原理
SVM损失函数解释
对于数据中的N个训练样本，每个训练样本i可以被表示为 ( x i , y i ) ( i = 1 , 2 , 3 , . . . . N ) (x_i,y_i)(i=1,2,3,....N) (xi,yi)(i=1,2,3,....N)其中xi是 ( x 1 i , x 2 i , x 3 i , . . . . x n i ) T (x_{1i},x_{2i},x_{3i},....x_{ni})^T (x1i,x2i,x3i,....xni)T这样的特征向量，每个样本总共含有n个特征。二分类标签的yi取值为{-1，1}。
特别的，当n为二时，有 i = ( x 1 i , x 2 i , y i ) T i=(x_{1i},x_{2i},y_i)^T i=(x1i,x2i,yi)T,由特征向量和标签组成。此时可以在二维平面上可视化这些样本
不妨让紫色标签为1，红色标签为-1。此时要在这个数据集上找到一个决策边界，也就是一条直线。即：
x 1 = a x 2 + b x_1=ax_2+b x1=ax2+b
变换形式：
0 = a x 2 − x 1 + b 0 = [ a , − 1 ] ∗ [ x 2 x 1 ] + b 0 = w T x + b 0=ax_2-x_1+b \\0=[a,-1]*\left [ \begin{matrix}x_2\\x_1\end{matrix} \right ]+b\\0=w^Tx+b 0=ax2−x1+b0=[a,−1]∗[x2x1]+b0=wTx+b
其中[a,-1]就是参数向量w，x就是特征向量，b是截距。这个表达式可以代表平面上的任何一条直线，当w和b固定时，给定一个唯一的x取值就可以确定一个点。由于目标是求解让边际最大的决策边界，所以就要求解参数向量w和截距b
显然，w方向与决策边界垂直
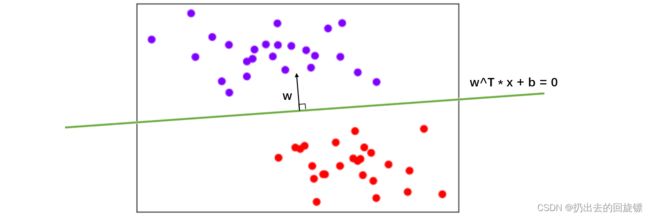
说明：
- 注意p、r的符号是提前人为规定的。这与决策边界平移以及样本点代入的正负都是无关的，只是为了推导和计算的简便我们规定而已，通常规定如下
标签是{-1,1}
决策边界以上的点，标签都为正，并且通过调整w和b的符号，让这个点在 w ⋅ b + b w\cdot b+b w⋅b+b 上得出的结果为正。
决策边界以下的点，标签都为负，并且通过调整w和b的符号，让这个点在 w ⋅ b + b w\cdot b+b w⋅b+b上得出的结果为负。
这种规定，不会影响对参数向量w 和截距b 的求解。
对于决策边界两边的超平面可以表示如下：
w ⋅ x + b = k , w ⋅ x + b = − k w\cdot x+b=k,w\cdot x+b=-k w⋅x+b=k,w⋅x+b=−k
两边同时除以k可以得到：
w ⋅ x + b = 1 , w ⋅ x + b = − 1 w\cdot x+b=1,w\cdot x+b=-1 w⋅x+b=1,w⋅x+b=−1
此时可以让这两条线分别过距离决策边界最近的点，这些点就称为“支持向量”，此时另紫色点为 x p x_p xp，红色的点位 x r x_r xr，可以得到：
w ⋅ x p + b = 1 , w ⋅ x r + b = − 1 w\cdot x_p+b=1,w\cdot x_r+b=-1 w⋅xp+b=1,w⋅xr+b=−1
两式相减为：
w ⋅ ( x p − x r ) = 2 w\cdot (x_p- x_r)=2 w⋅(xp−xr)=2
( x p − x r ) (x_p- x_r) (xp−xr)可以理解为两点之间的连线，此时可以有
w ⋅ ( x p − x r ) ∣ ∣ w ∣ ∣ = 2 ∣ ∣ w ∣ ∣ d = 2 ∣ ∣ w ∣ ∣ \frac{w \cdot(x_p- x_r)}{||w||}=\frac{2}{||w||}\\d=\frac{2}{||w||} ∣∣w∣∣w⋅(xp−xr)=∣∣w∣∣2d=∣∣w∣∣2
所以要最大化d，就是最小化w。可以转换成下面这个函数的最小值：
f ( w ) = ∣ ∣ w ∣ ∣ 2 2 f(w)=\frac{||w||^2}{2} f(w)=2∣∣w∣∣2
模长加平方是因为本来距离带个跟号，此时就得到了SVM函数的最初形态：
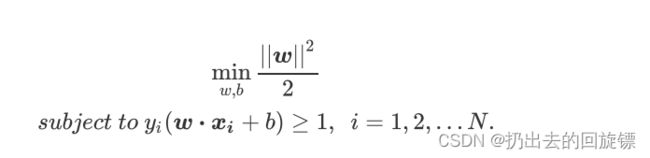
函数间隔与几何间隔
几何间隔的本质是点xi到超平面 ( w , b ) (w,b) (w,b)即决策边界的带符号的距离
几何间隔表示如下：
γ i = y i ( w ∣ ∣ w ∣ ∣ x i + b ∣ ∣ w ∣ ∣ ) \gamma_i=y_i(\frac{w}{||w||}x_i+\frac{b}{||w||}) γi=yi(∣∣w∣∣wxi+∣∣w∣∣b)
说明：
- ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣的模长就是 a 2 + b 2 \sqrt{a^2+b^2} a2+b2,将边界点代入通过点到之间距离公式就能得到距离
函数间隔可以表示为分类预测的正确性以及确信度
对于给定数据集T和超平面（w，b），定义超平面(w,b)关于样本点 ( x i , y i ) (x_i,y_i) (xi,yi)的函数间隔为： γ i = y i ( w x i + b ) \gamma_i=y_i({w}x_i+{b}) γi=yi(wxi+b)
将损失函数转换为拉格拉日乘数形态
最初形态的损失函数分为两部分：需要最小化的函数以及参数求解之后必须满足的约束条件，所以可以使用拉格朗日乘数法进行合并求解，表现形式如下：
L ( w , b , a ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 N α i ( y i ( w ⋅ x i + b ) − 1 ) ( α i ≥ 0 ) L(w,b,a)=\frac{1}{2}||w||^2-\sum_{i=1}{N}\alpha_i(y_i(w\cdot x_i+b)-1)(\alpha_i\geq0) L(w,b,a)=21∣∣w∣∣2−i=1∑Nαi(yi(w⋅xi+b)−1)(αi≥0)
说明：
- 损失函数是二元的，并且约束条件在参数w和b下是线性的，求解这样的损失函数被称为“凸优化问题”。拉格朗日乘数法就是用来解决凸优化问题的方法
- 目标是要通过先最大化，再最小化它来求解向量w和截距b的值，即 m i n w , b m a x α i ≥ 0 L ( w , b , α ) ( α i ≥ 0 ) \mathop{min}\limits_{w,b}\mathop{max}\limits_{\alpha_i \geq0}L(w,b,\alpha)(\alpha_i\geq0) w,bminαi≥0maxL(w,b,α)(αi≥0)
当 y i ( w ⋅ x i + b ) > 1 y_i(w\cdot x_i+b)>1 yi(w⋅xi+b)>1,函数的第二部分为正， 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}||w||^2 21∣∣w∣∣2减正数，若要最大化 L ( w , b , a ) L(w,b,a) L(w,b,a)，就必须 α \alpha α取0
当 y i ( w ⋅ x i + b ) < 1 y_i(w\cdot x_i+b)<1 yi(w⋅xi+b)<1,函数的第二部分为正， 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}||w||^2 21∣∣w∣∣2减负数数，若要最大化 L ( w , b , a ) L(w,b,a) L(w,b,a)，就必须 α \alpha α取正无穷
将拉格朗日函数转换为拉格朗日对偶函数
如果我们尝试用正常的求偏导来求拉格朗日的极值，过程如下：
可以看到求解结果中都含有未知数 a i a_i ai，因此无法求解出来。而有一种拉格朗日对偶函数的形式，只带有 a i a_i ai>此时可以利用它求解出拉格朗日乘数 a i a_i ai，然后代入推导即可
对偶函数求解过程如下：
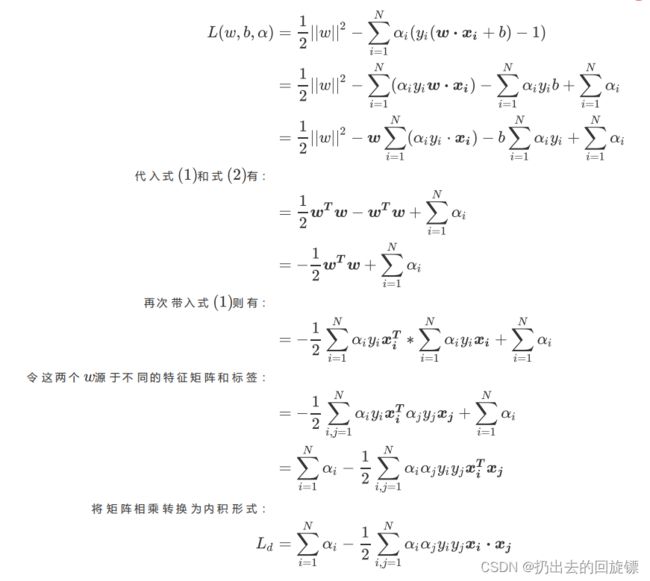
其中 L d L_d Ld就是我们的对偶函数。对于所有存在对偶函数的拉格朗日函数有对偶差异如下所示：
Δ = min x L ( x , α ) − max α g ( α ) \Delta= \min\limits_{x}L(x,\alpha)-\max\limits_{\alpha}g(\alpha) Δ=xminL(x,α)−αmaxg(α)
则对于 L ( w , b , α ) L(w,b,\alpha) L(w,b,α)和 L d L_d Ld,有：
Δ = min w , b max a ≥ 0 L ( w , b , α ) − max a i ≥ 0 L d \Delta= \min\limits_{w,b}\max\limits_{a\geq0}L(w,b,\alpha)-\max\limits_{a_i\geq0}L_d Δ=w,bmina≥0maxL(w,b,α)−ai≥0maxLd
推导 L d L_d Ld对偶函数的过程就是求解 L ( w , b , α ) L(w,b,\alpha) L(w,b,α)的最小值，所以有：
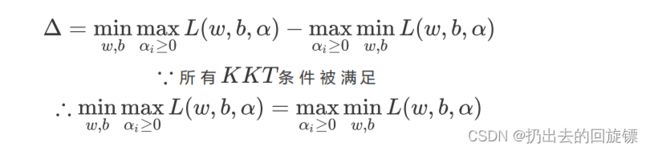
最终的目标函数变化为：
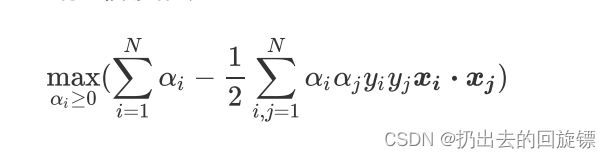
说明：
- 对于任何一个拉格朗日函数 L ( x , α ) = f ( x ) + ∑ i = 1 q α i h i ( x ) L(x,\alpha)=f(x)+\sum_{i=1}{q}\alpha_ih_i(x) L(x,α)=f(x)+∑i=1qαihi(x)都存在有一个与它对应的对偶函数 g ( α ) g(\alpha) g(α),只带有拉格朗日乘数 α \alpha α作为唯一的参数
- 对偶差异，即拉格朗日的最优解与其对偶函数的最优解之间的差值。当满足KTT条件时，对偶差异为0，说明拉格朗日函数与期对偶函数之间存在强对偶关系，此时可以通过求解对偶函数的最优解来替代求解原始函数的最优解
如果 L ( x , α ) L(x,\alpha) L(x,α)的最佳解存在并且可以表示为 min x L ( x , α ) \min\limits_{x}L(x,\alpha) xminL(x,α),并且对偶函数的最优解也存在并表示为 max α g ( α ) \max\limits_{\alpha}g(\alpha) αmaxg(α)，对偶差异表示为 Δ = min x L ( x , α ) − max α g ( α ) \Delta= \min\limits_{x}L(x,\alpha)-\max\limits_{\alpha}g(\alpha) Δ=xminL(x,α)−αmaxg(α)
KTT条件如下：
1：所有参数的一阶导数为0
2：约束函数中函数本身小于等于0
3：拉格朗日乘数大于等于0
4：约束条件和拉格朗日乘数之间有一个为0
对于这里的损失函数 L ( w , b , α ) L(w,b,\alpha) L(w,b,α)而言，KTT条件的操作如下：
1：首先让拉格朗日函数上对参数w和b求导为0：
2：通过先求解最大值再求解最小值的方式使得函数天然满足：
3：只选择支持向量代入可以满足
后续步骤
通过SMO或者二次规划来求解 α \alpha α（暂时不解释),之后就能将w和b求解出来，最后获得决策边界的表达式如下：
f ( x t e s t = s i g n ( w ⋅ x t e s t + b ) = s i g n ( ∑ i = 1 N α i y i x i ⋅ x t e s t + b ) f(x_{test}=sign(w\cdot x_{test}+b)=sign(\sum_{i=1}{N}\alpha_iy_ix_i\cdot x_test+b) f(xtest=sign(w⋅xtest+b)=sign(i=1∑Nαiyixi⋅xtest+b)
其中 x t e s t x_{test} xtest是任意测试样本，sign（h）在h>0时返回1，h>0时返回-1
3.线性SVM决策过程的可视化
可视化决策边界、支持向量、以及两个超平面
步骤一：导入库并实例可视化数据集
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
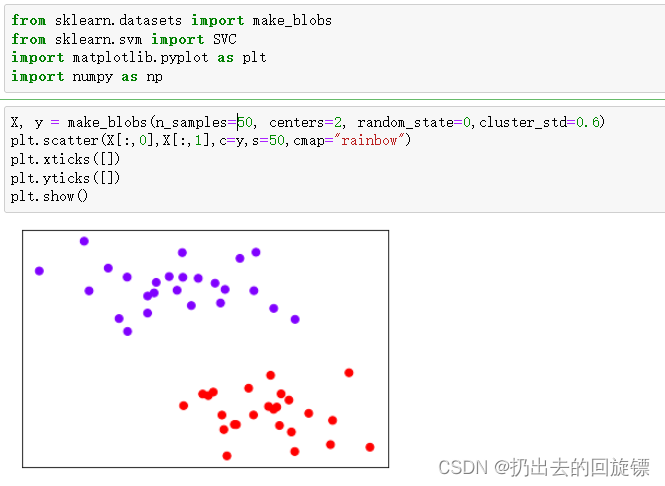
X, y = make_blobs(n_samples=50, centers=2, random_state=0,cluster_std=0.6)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.xticks([])
plt.yticks([])
plt.show()
步骤二:绘制网格流程
#获取平面对象
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca()
#网格化
xlim = ax.get_xlim()
ylim = ax.get_ylim()
axisx = np.linspace(xlim[0],xlim[1],30)
axisy = np.linspace(ylim[0],ylim[1],30)
axisy,axisx = np.meshgrid(axisy,axisx)
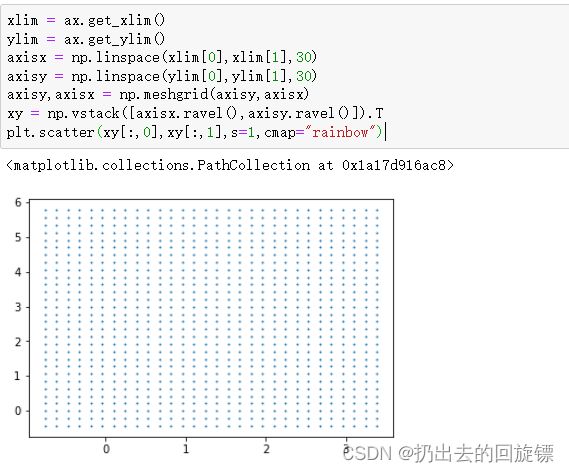
xy = np.vstack([axisx.ravel(),axisy.ravel()]).T
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
meshgrid将特征向量广播，获取y.shape*x.shape这么多的横坐标和纵坐标
vstack将多个结构一致的一维数组堆叠形成多维数值
步骤三：绘制决策边界
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca()
clf = SVC(kernel = "linear").fit(X,y)
z = clf.decision_function(xy).reshape(axisx.shape)
ax.contour(axisx,axisy,z
,colors="k"
,levels=[-1,0,1]
,alpha=0.5
,linestyles=["--","-","--"])
contour函数：绘制等高线
| 参数 | 含义 |
|---|---|
| X,Y | 二维平面上所有点的横纵坐标值，一般要求形状与Z相同。如果XY都是一维，则Z的结构必须为（len(y),len(x))。默认X=range(Z.shape[1],Y=range(Z.shpae[0]） |
| Z | 平面上所有点所对应高度 |
| levels | 确定等高线的数量和位置，列表或数组必须按照递增顺序排序 |
步骤四：绘制某一点的等高线
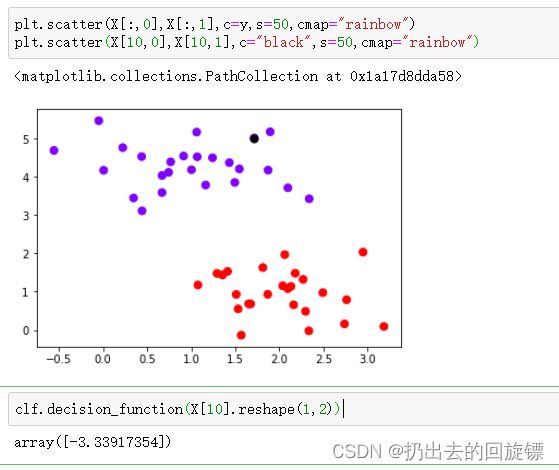
#选择一个点并计算它到决策边界的距离
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.scatter(X[10,0],X[10,1],c="black",s=50,cmap="rainbow")
clf.decision_function(X[10].reshape(1,2))
绘制等于这个距离的线
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax=plt.gca()
ax.contour(axisx,axisy,z
,colors="k"
,levels=[-3.33917354]
,alpha=0.5
,linestyles=["--"])
步骤五：包装绘图函数
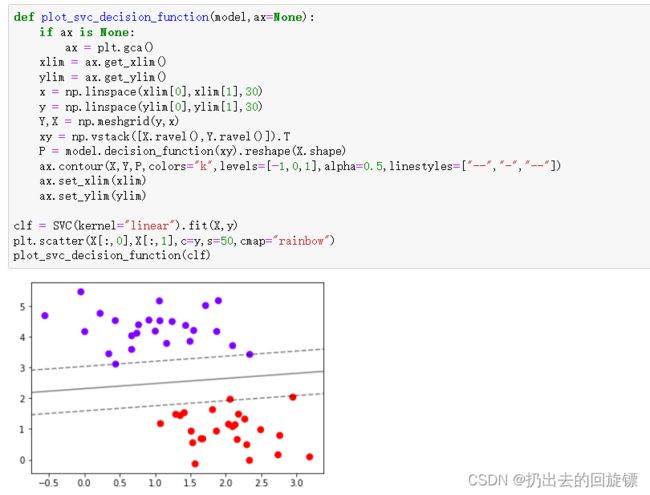
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(),Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X,Y,P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
clf = SVC(kernel="linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
步骤六：探索模型
#返回根据决策边界返回的分类结果
clf.predict(X)
#返回给定测试集的平均准确度
clf.score(X,y)
#返回支持向量
clf.support_vectors_
#返回每个类中支持向量的个数
clf.n_support_
如果数据是非线性的呢？
步骤一：生成非线性数据集
from sklearn.datasets import make_circles
X,y = make_circles(100,factor=0.1,noise=.1)
X.shape
y.shape
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.show()
步骤二：尝试用之前的函数来绘制决策边界
clf = SVC(kernel="linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
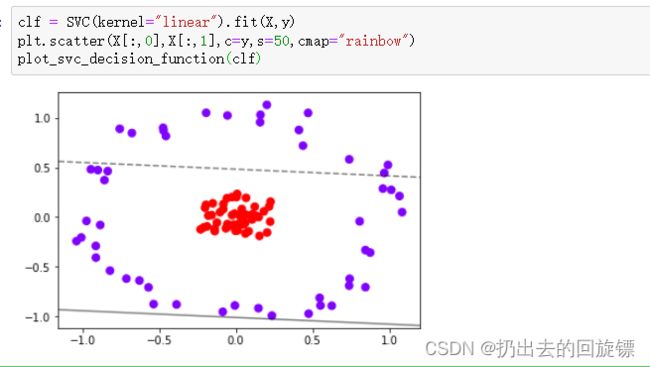
很明显，效果不好。可以将数升维来处理
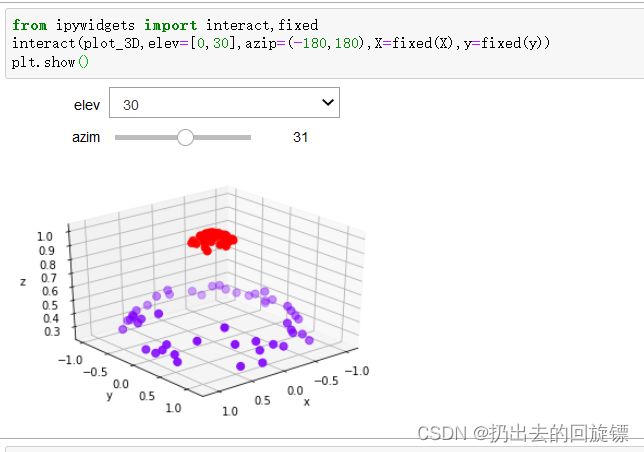
步骤三：升维处理并绘制3d图像
r = np.exp(-(X**2).sum(1))
rlim = np.linspace(min(r),max(r),100)
from mpl_toolkits import mplot3d
def plot_3D(elev=30,azim=30,X=X,y=y):
ax=plt.subplot(projection="3d")
ax.scatter3D(X[:,0],X[:,1],r,c=y,s=50,cmap='rainbow')
ax.view_init(elev=elev,azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
plt.show()
plot_3D()
这种变换称为核变换。从而引入新的概率：核函数
其他：
jupyter notebook专属的可控3D图
