【机器学习（四）】分类问题与logistic回归模型

声明：本文是以吴恩达机器学习系列课程为学习对象而作的学习笔记。本文对应P32-P36、P38。

情景引入

在前面几篇文章中，我们提到了判断邮件是否为垃圾邮件的例子，以及良性与恶性肿瘤的例子。
在所有的这些问题中，我们尝试预测的变量y，都是可以有两个取值的变量——0或1。我们用0来表示的这一类还可以叫做”负类“，用1来表示的这一类还可以叫做正类。

现在我们要从只包含0和1两类的分类问题开始。

假设陈述——logistic回归

试想：如果如此一个问题运用前期所提到的回归函数来拟合的话，光想象都离谱。因此，我们需要换一种拟合方式。

我们希望我们的分类器的输出值在0和1之间。因此，我们来提出一个假设，来满足该性质，让这些估算值在0和1之间。

当我们用线性回归的方式时，这是假设的形式：

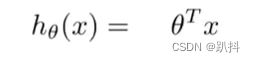
对于logistic回归，我们将上式修改一点点：

我们定义函数g如下：

将上述两式联立得到：

其函数图像如下：

当z趋于正无穷时，g(z)趋近于1；当z趋于负无穷时，g(z)趋于0。
因为g(z)的值在0和1之间，也就得到：h(x)一定在0和1之间。

在拥有了这个假设函数后，我们要做的就是用参数θ拟合我们的数据。
所以拿到一个训练集后，我们需要给参数θ选定一个值，假设会帮我们做出预测。

简单而言，我们现在的目标是判断一个值更加趋于正类还是负类。因此，我们需要一个值域为[0,1]的假设函数来判断，可以将其得到的函数值看作一个概率：当得到的数越趋近于1，则说明更可能为正类；反之类似。以下时吴老师给出的板书解释：

其中右下角第一个等式的解释是：给定参数θ，对于具有x特征的病人，y=0的概率，与同样给定参数θ，同样具有特征x的病人，y=1的概率相加，和为1。因为结果只有0和1两种可能。

决策边界

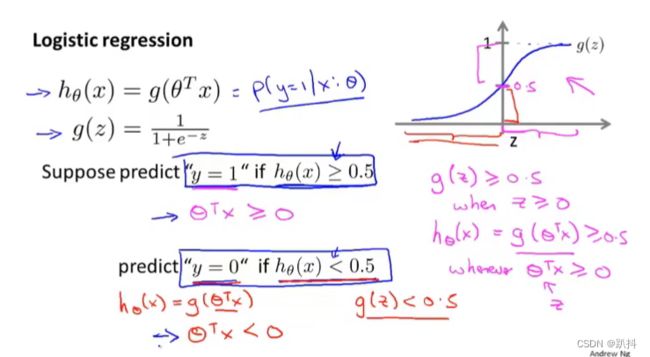
如图，我们设定：函数值大于等于0.5时，预测为1；函数值小于0.5时，预测为0。由图像可知，上句等价于：当θ^T x大于等于0时，预测为1；当θ^T x小于0时，预测为0。

我们先来看一个例子：
现在假设我们有一个训练集，其图像与假设函数如下：

假设我们已经拟合好了参数：θ_0=-3,θ_1=θ_2=1。这说明我的参数向量θ等于[-3,1,1]。

现在我们来找出假设函数何时将预测y等于1，何时又将预测y等于0。利用我们上一张图片的公式，得到如下图所示：

简而言之，其实就是将θ_0=-3,θ_1=θ_2=1代入式子得到上述不等式。同时，该不等式还定义了一条直线：

也就是说，该直线上面的半平面，即右上方的所有部分即为我们假设函数预测y等于1的区域。 同时，直线左下方的部分就是假设函数预测y=0的区域。
而这条线被称为决策边界。决策边界时假设函数的一个属性，决定于参数，其并非是数据集的属性。

代价函数

下图是监督学习问题中的logistic回归模型的拟合问题

我们有一个训练集，里面有m个训练样本，每个样本用n+1维的特征向量表示，符合y属于{0，1}的特征，即所有的标签y不是0就是1。假设函数为h_θ(x)。现在要解决的问题是，对于给定的训练集，我们如何选择参数θ？

我们运用先前做线性回归模型的代价函数，并对其做一些调整：

我们设置一个cost，修改如下：

如果我们可以最小化函数J里面的这个代价函数，它也能工作。但如果我们使用这个代价函数，他会变成参数θ的非凸函数。

你会发现，如果你把梯度下降法用在这样一个函数上，不能保证它会收敛到全局最小值。相对的，我们希望代价函数J(θ)是一个凸函数，或者说是一个单弓型函数，它可以保证收敛到全局最小值：

问题出在：如果使用这个平方代价函数，使用中间那个非常非线性的signoid函数会导致J(θ)函数成为一个非凸函数。

所以我们要做的是另外找一个不同的代价函数，使得其为凸函数，如下所示：

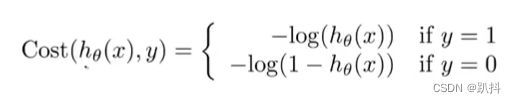
当y=1时，函数图像如下：

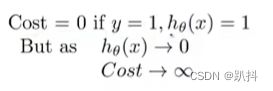
当y=0时，函数图像如下：

现在我们将这个代价函数进行优化，需要用一种方法将y=1和y=0两个式子合并成一个等式。

当y分别等于0和1时，代价函数分别等于上述两个等式。

现在我们要做的是：最小化关于θ的代价函数J(θ)，这样我们才能为训练集拟合出参数θ。因此我们又要用到梯度下降法了。

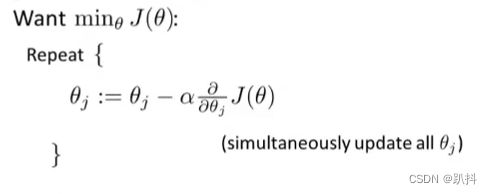
要注意的是：即使更新参数的规则看起来基本相同，由于假设的定义(h_θ(x))发生了变化，logistic回归和线性回归的梯度下降实际上是两个完全不同的东西。

多元分类——一对多

假如说你现在需要一个学习算法，自动地将邮件归类到不同的文件夹里，或者说可以自动地加上标签。所以你有不同的文件夹或者不同的标签来区分各类例如工作、朋友、家庭、兴趣的邮件。我们就有了一个包含四个分类的问题

相较于先前的一个二元分类问题，对于一个多类别分类问题，我们的数据集如下：

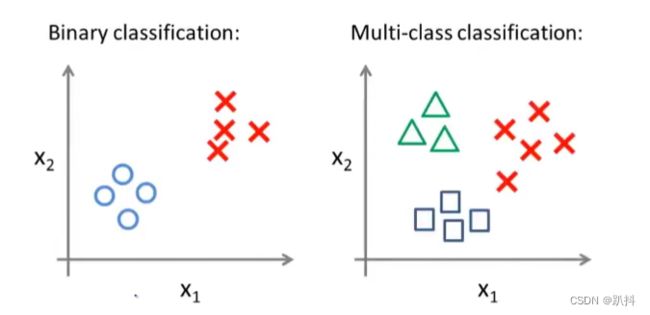
面对如此一个包含三个类别的训练集，我们要做的就是：将这个训练集转化为三个独立的二元分类问题。

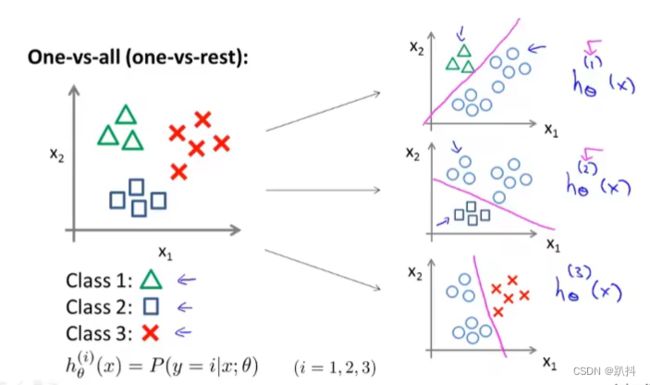
我们拟合出三个分类器，对于i等于1，2，3我们拟合分类器h_θ^(i)(x)，来尝试估计出给定x和θ时，y=i的概率。