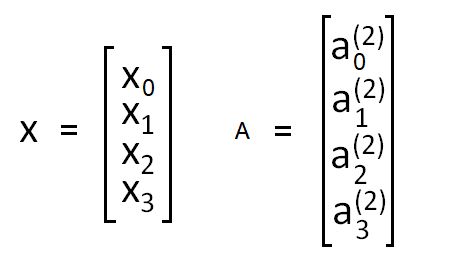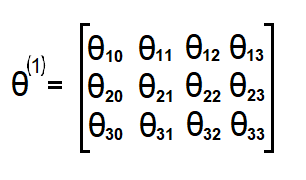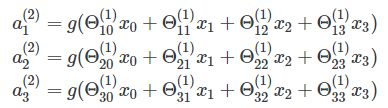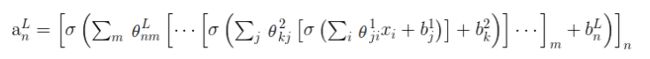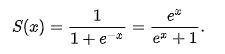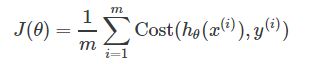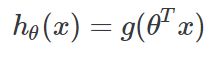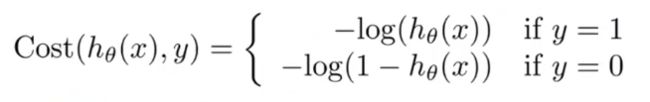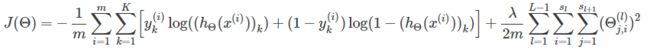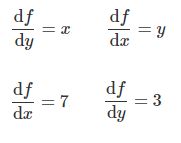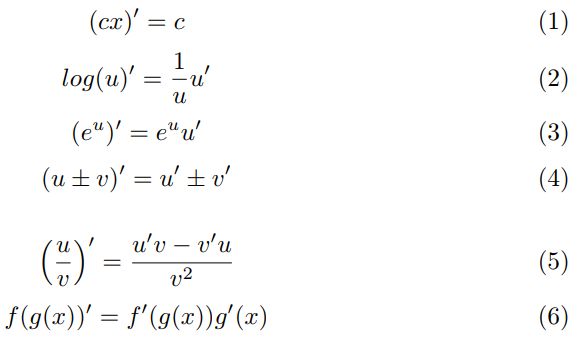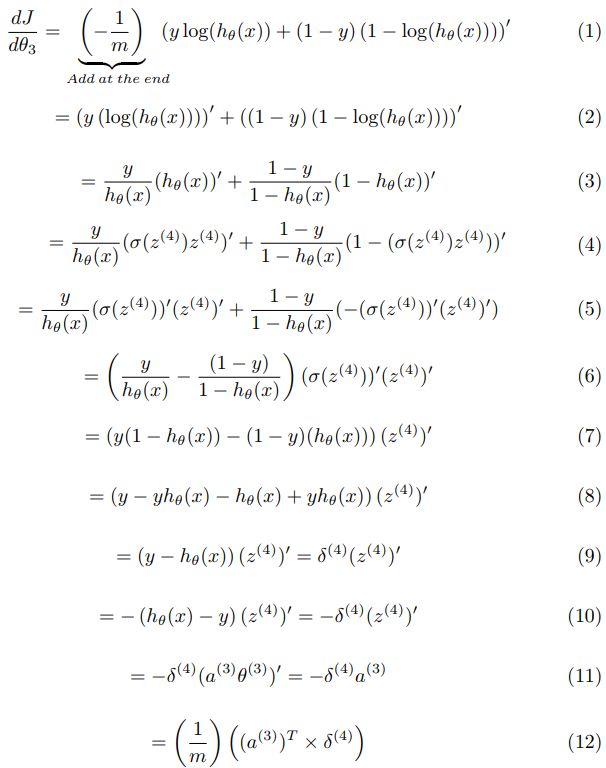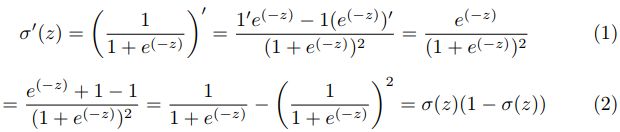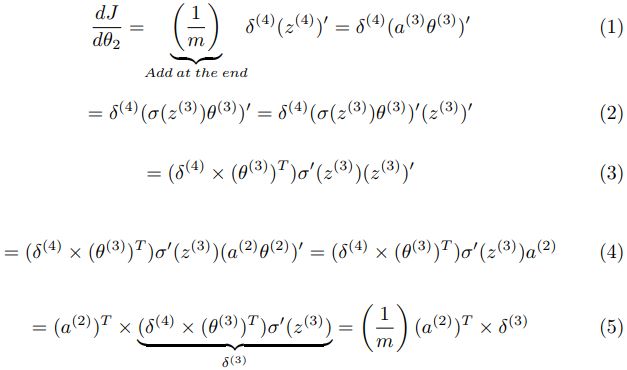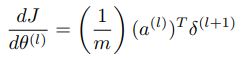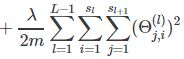神经网络和反向传播算法的详细解释，深度学习基础

本文通过以下8个部分来详细解释神经网络的一些基本概念：

• 模型表示（Model Representation）
• 模型的数学表示（Model Representation Mathematics）
• 激活函数（Activation Functions）
• 偏置节点（Bias Node）
• 损失函数（Cost Function）
• 前向传播计算（Forward Propagation Calculation）
• 反向传播算法（Backpropagation Algorithm）
• 代码实现（Code Implementation）

1. 模型表示（Model Representation）

人工神经网络是受构成动物大脑的生物神经网络启发而产生的计算系统。这类系统通过实例来“学习”并执行任务，通常不需要编写任何特定于任务的规则。

图1：神经网络结构

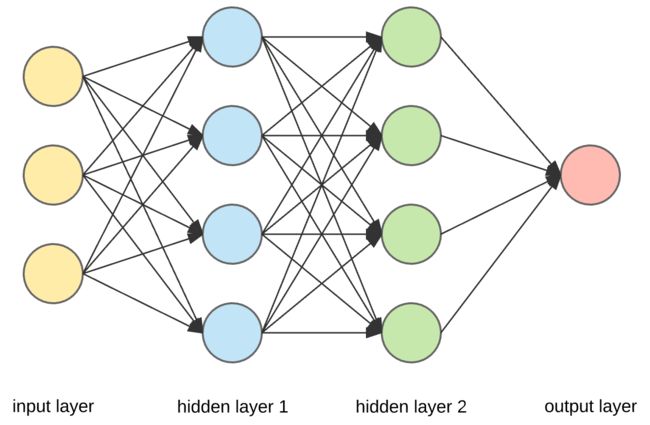
神经网络由三层构成：

• 输入层：神经网络的原始数据；
• 隐藏层：输入层和输出层之间的中间层，所有计算都在这里完成；
• 输出层：对给定的输入产生结果。

上图中有3个黄色的圆圈，表示输入层，通常记作向量$X$。有4个蓝色和4个绿色的圆圈表示隐藏层，这些圆圈代表了“激活（activation）”节点，通常表示为$W$或$\theta$。红色的圆圈是输出层或预测值（可以有多个输出）。

每个节点与下一层的每个节点连接，每个连接（黑色箭头）具有特定的权值（weight）。权值可以看作是该节点对下一层节点的影响。如果我们查看一个节点，它将看起来像这样：

图2：神经网络中的节点

让我们看看顶部的蓝色节点（图1），上一层（黄色）的所有节点都与它连接，所有这些连接都表示权重（影响）。 当将黄色层中的所有节点值乘以它们的权重并汇总后，将为顶部蓝色节点提供一些值。蓝色节点具有预定义的“激活”函数（Activation Function，图2中的unit step function），该函数根据汇总值定义该节点是否被“激活”或如何“激活”。值为1的附加节点称为“偏置”节点。

2. 模型的数学表示（Model Representation Mathematics）

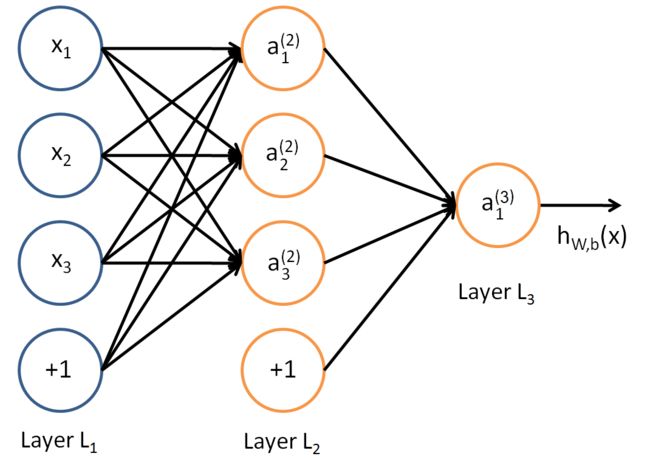
为了理解数学方程，将使用一个更简单的神经网络模型。该模型有4个输入节点（3+1个偏置节点），含有4个节点（3+1个偏置节点）的隐藏层和一个输出节点。

图3：神经网络中的节点

我们要偏置节点分别标记为$x_0$和$a_0$，则可用向量表示为：

图4：X（输入层）和A（隐藏层）向量

权重（箭头）通常记为$\theta$或$W$。在这种情况下，我将记为$\theta$。输入层和隐藏层之间的权重将表示为3x4的矩阵。而隐藏层与输出层之间的权值为1x4的矩阵。

如果网络在第$j$层有$a$个单元，在第$j+1$层有$b$个单元，则${\theta }_j$的维度为$b\times (a+1)$。

图5：层1的权重矩阵（θ）

接下来，我们要计算隐藏层的“激活”节点。为此，我们需要将输入向量X和第一层的权重矩阵${\theta }^1$相乘（$X\ast {\theta }^1$），然后应用激活函数g。我们得到的是:

图6：计算激活节点

然后通过将隐藏层向量与第二层的权重矩阵$\theta$相乘$A\ast \theta$，我们得到假设函数的输出：

图7：计算输出节点的值

这个例子中只包含一个隐藏层和4个节点。如果我们尝试对具有多个隐藏层且每个层中有多个节点的神经网络时，我们将得到以下公式：

图8：计算节点值的一般函数

表示含有n个节点的L个层，且第L-1层含有m个节点。

3. 激活函数（Activation Functions）

在神经网络中，激活函数根据加权来决定给定节点是否应该被“激活”。将这个加权总和的值定义为z。在本节中，我将解释“阶跃函数（Step Function）”和“线性函数（Linear Function）”不起作用的原因，并讨论最流行的激活函数之一“Sigmoid函数”。

3.1 阶跃函数（Step Function）

第一种是使用“阶跃函数”（离散的输出值），我们定义阈值和：

$$\begin{array}{rl}& if(z>threshold)—激活节点（值为1）\\ & if(z<threshold)—不激活节点（值为0）\end{array}$$

这个函数的缺点在于节点只能输出0或1，如果我们想要映射多个输出类（节点），就会遇到问题，导致我们无法正确地分类/决定。

3.2 线性函数（Linear Function）

另一种是定义“线性函数”并得到一个输出值范围。

$$y=ax$$

然而，在神经网络中只使用线性函数会导致输出层为线性函数，因此我们无法映射任何非线性数据。证明如下：

$$f(x)=x+3$$

$$g(x)=2x+5$$

然后通过函数复合我们得到：

$$g(f(x))=2(x+3)+5=2x+11$$

这依然是一个线性函数。

3.3 Sigmoid函数

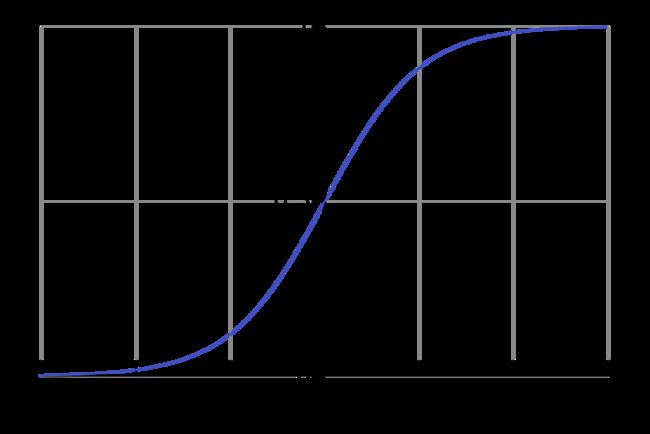
Sigmoid函数是目前应用最广泛的激活函数之一，它的方程如下式所示：

图9：Sigmoid函数

图10：Sigmoid函数

它有多种属性，这使得它很受欢迎：

• 它是非线性的函数；
• 值在(0,1)之间；
• 在x轴上的(-2,2)之间，函数非常陡峭，这导致函数倾向于分类1或0。

由于这个属性，它允许节点取0到1之间的任何值。最后，在有多个输出类别的情况下，这将导致每个输出类别的“激活”概率不同。 然后，我们将选择“激活”（概率）值最高的那个。

4. 偏置节点（Bias Node）

使用偏置节点通常对于创建成功的学习模型至关重要。 简而言之，偏置量允许将激活函数向左或向右移动，并有助于更好地适应数据（更好的预测函数作为输出）。

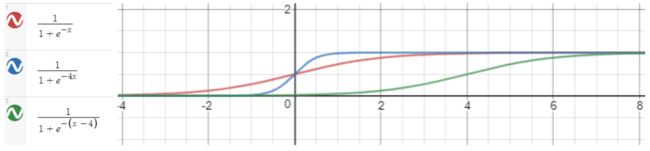
下面绘制了3个Sigmoid函数，你可以在其中注意到变量x与某个值相乘/相加/相减会如何影响该函数。

• 乘以x -使函数更陡峭；
• 加/减x -将函数左移/右移。

图11：不同的Sigmoid函数

5. 损失函数（Cost Function）

首先，定义损失函数的一般公式。 此函数表示误差之和，预测值与实际（标签）值之间的差。

图12：一般的损失函数

由于这是一种分类问题，y只能取离散值{0,1}，它只能取其中的一个值。例如，如果我们分类狗(类1)，猫(类2)和鸟(类3)的图像。如果输入的图像是狗。对于dog类，输出类的值为1，对于其他类，输出类的值为0。

这意味着我们希望我们的假设满足：

图13：假设函数的取值范围

这就是为什么我们把假设定义为：

图14：假设函数

这里g是Sigmoid函数，因为此函数f的取值范围是(0,1)。

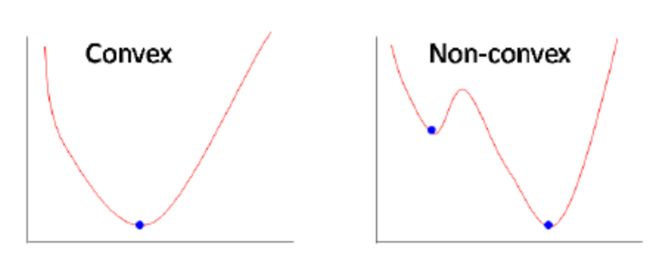
我们的目标是优化损失函数，因此我们需要找到最小的$J(\theta )$。 但是，Sigmoid函数是“非凸”函数（“图像15”），这意味着存在多个局部最小值。 因此，不能保证收敛到（找到）全局最小值。 我们需要的是梯度下降算法中的“凸”函数，以便能够找到全局最小值（使$J(\theta )$最小）。 为了做到这一点，我们使用$log$函数。

图15：凸函数 vs 非凸函数

这就是为什么我们在神经网络中使用以下损失函数：

图16：神经网络的损失函数

如果标签值y=1，则假设为$-log(h(x))$否则为$-log(1-h(x))$

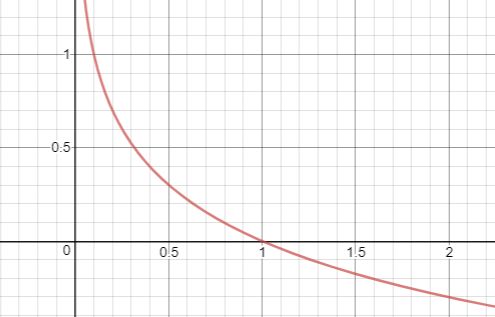
如果我们看一下函数图，就会非常直观。我们先来看y=1的情况，则$-log(h(x))$就像下图所示。我们只对x轴上的(0,1)区间感兴趣，因为假设只能取这个范围内的值("图13 ")。

图17：损失函数-log(h(x))

从图中可以看到，如果y = 1并且h（x）接近值1（x轴），则损失函数的值接近0（h（x）-y为0），因为这是正确的预测。 否则，如果h（x）接近0，则损失函数将变为无穷大。

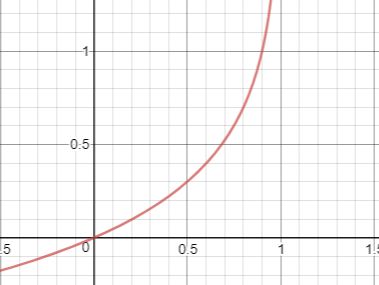
在另一种情况下，y=0，损失函数是-log(1-h(x))：

图18：损失函数-log(1-h)

从图中我们可以看出，如果h(x)趋近于0，那么代价也会趋近于0，因为这也是正确的预测。

由于y(标签值)总是等于0或1，我们可以把损失函数写在一个方程中。

图19：损失函数方程

如果我们把我们的损失函数完全写出来，加上求和，我们会得到：

图20：一个输出节点的损失函数

这是在神经网络的输出层中只有一个节点的情况下。 如果我们将其推广到多个输出节点（多类分类），我们将得到：

图21：一般的损失函数

方程的右侧部分表示损失函数的“正则化”，通过减小$\theta$的大小来防止数据“过度拟合”。

6. 前向传播计算（Forward Propagation Calculation）

前向传播的过程实际上是根据给定的输入获得神经网络的输出值。该算法用于计算损失值（cost value）。 它所做的是与第2节“模型的数学表示”中描述的过程相同的数学过程， 最终得到假设值“图7”。

在得到h(x)值(假设)之后，我们使用损失函数方程(“图21”)来计算给定输入集的损失。

图22：计算前向传播

这里我们可以看到前向传播是如何工作的，以及神经网络是如何产生预测的。

7. 反向传播算法（Backpropagation Algorithm）

我们要做的是使用$\theta$（权重）的最优值集合来最小化损失函数$J(\theta )$。 反向传播是我们用来计算$J(\theta )$的导数的一种方法。

然后，该导数值在梯度下降算法（“图像23”）中用于计算神经网络的$\theta$值，从而使损失函数$J(\theta )$最小。

图23：梯度下降的一般形式

反向传播算法有5步：

1. 设$a(1)=X$，用于训练；
2. 执行前向传播并计算其他层的$a(l)(l=2\dots L)$；
3. 使用$y$并计算最后一层的增量值$\delta L=h(x)-y$；
4. 向后计算每一层的$\delta (l)$值（在“反向传播背后的数学”一节中介绍）；
5. 计算每一层的导数值$\Delta (l)=(a(l){)}^T\cdot \delta (l+1)$，它表示损失函数$J(\theta )$对于层$l$的权重系数$\theta (l)$的导数。

反向传播是关于确定改变权值如何影响神经网络的总体损失。

它所做的是在神经网络中反向传播“误差”。 在回溯的过程中，它查找每个权重对整体“误差”的贡献程度。 对整体“误差”贡献更大的权重将具有较大的导数值，这意味着它们在计算“梯度”下降时的变化将更大。

现在我们已经知道了反向传播算法在做什么，我们可以更深入地研究它背后的概念和数学原理。

7.1 为什么要求导数？

函数$J(\theta )$在每个变量（这里为权重$\theta$）上的导数，表示的是该函数相对于该变量的敏感度，或者更改变量如何影响函数值。

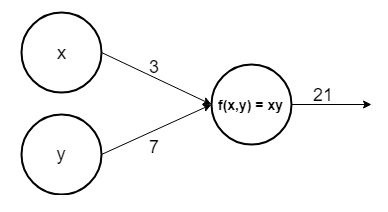
让我们来看一个简单的神经网络例子：

图24：一个简单的神经网络

这里有两个输入节点x和y，输出函数是计算x和y的乘积，现在我们可以计算两个节点的导数：

图25：函数f(x,y)=xy的导数

相对于x的导数表示，如果x增加某个值$\epsilon$，那么它将使函数增加$7\epsilon$，而相对于y的导数表示，如果y值增加某个值$\epsilon$，则它将使函数增加$3\epsilon$。

根据我们的定义，反向传播算法是针对每个$\theta$权重参数计算损失函数的导数。通过这样做，我们确定损失函数$J(\theta )$对这些$\theta$权重参数中的每一个有多敏感。 它还有助于我们确定在计算梯度下降时应改变每个$\theta$权重参数的程度。 因此，最后我们获得了最适合我们数据的模型。

7.2 反向传播背后的数学原理（Math behind Backpropagation）

我们将以下面的神经网络模型为出发点，推导出方程。

图26：神经网络

在这个模型中，我们有3个输出节点(K)和2个隐藏层。如前所述，神经网络的损失函数为：

图27：一般的损失函数

我们需要的是针对每个$\theta$参数计算$J(\theta )$的导数。 由于将使用矢量化实现（矩阵乘法），因此我们将省略中间部分。 同样，我们可以省略正则化（上面等式的右部分），最后将单独进行计算。 由于它是加法，因此可以独立计算导数。

我们首先定义将要使用的导数规则：

图28：导数规则

现在我们定义神经网络模型的基本方程，其中$l$是层的符号，且$L$是最后一层。

图29：初始的神经网络模型方程

在我们的例子中，$L$的值是4，因为我们的模型中有4层。我们先来计算一下对第3层和第4层的权重的导数。

图30：第3层和第4层之间权重参数θ的导数

步骤(6)- Sigmoid导数

为了解释步骤(6)，我们需要计算sigmoid函数的偏导数。

图31：Sigmoid函数的导数

对于最后一层$L$，我们有：

图32：输出层方程

所以：

图33：输出层方程

步骤（11）—摆脱求和（$\sum$）

同样在最后一步（11）中，我们需要将$\delta$与$a$的转置相乘才能摆脱求和（训练示例为1…m）。

• $\delta$-矩阵维度：[number_of_training_examples, output_layer_size]，因此这也意味着我们将摆脱第二个求和（输出节点数为1…K）；
• $a$-矩阵维度：[hidden_layer_size, number_of_training_examples]。

现在，我们继续第二和第三层之间$\theta$参数的求导。 对于此推导，我们可以从步骤（9）（“图片30”）开始。 由于$\theta (2)$在$a(3)$函数内部，我们在计算导数时需要使用“链式法则”（“图像28”上的导数规则的步骤（6））。

图34：第2层和第3层之间权重θ的导数

现在我们得到了第二层和第三层之间的$\theta$参数的导数。 我们要做的是计算输入层和第二层之间的$\theta$参数导数。这样，将重复相同的过程（方程式），因此我们可以得出一般的$\delta$和导数方程。 再次，我们从步骤（3）继续（“图34”）。

图35：输入层和第2层之间权重θ的导数

从上面的方程式中，我们可以导出$\delta$参数的方程式和$\theta$参数的导数。

图36：δ的递归方程

图37：l层方程中相对于θ的J(损失)的导数

最后，我们得到三个矩阵，其维数与θ权重矩阵相同，并为每个θ参数计算出导数。

7.3 添加正则项

如前所述，需要进行正则化，以防止模型过度拟合数据。 我们已经为损失函数定义了正则项，即“图21”中所定义方程的右侧部分。

图38：损失函数的正则项

为了增加梯度的正则化(偏导数)，我们需要计算上面正则项的偏导数。

图39：梯度的正则化方程（偏导数）

这意味着将来自每一层的所有$\theta$值之和与相对于$\theta$的偏导数相加。

8. 代码实现

我们现在可以在代码中实现所有方程,我们会计算损失和导数（使用反向传播），所以我们可以使用它们在梯度下降算法中来为我们的模型优化参数。

function [J grad] = nnCostFunction(nn_params, ...
                                   input_layer_size, ...
                                   hidden_layer_size, ...
                                   num_labels, ...
                                   X, y, lambda)
%NNCOSTFUNCTION Implements the neural network cost function for a two layer
%neural network which performs classification
%   [J grad] = NNCOSTFUNCTON(nn_params, hidden_layer_size, num_labels, ...
%   X, y, lambda) computes the cost and gradient of the neural network. The
%   parameters for the neural network are "unrolled" into the vector
%   nn_params and need to be converted back into the weight matrices.
%
%   The returned parameter grad should be a "unrolled" vector of the
%   partial derivatives of the neural network.
%

% Reshape nn_params back into the parameters Theta1 and Theta2, the weight matrices
% for our 2 layer neural network
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
                 hidden_layer_size, (input_layer_size + 1));

Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
                 num_labels, (hidden_layer_size + 1));

% Setup some useful variables
m = size(X, 1);

% You need to return the following variables correctly
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));

% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the code by working through the
%               following parts.
%
% Part 1: Feedforward the neural network and return the cost in the
%         variable J. After implementing Part 1, you can verify that your
%         cost function computation is correct by verifying the cost
%         computed in ex4.m
%
% Part 2: Implement the backpropagation algorithm to compute the gradients
%         Theta1_grad and Theta2_grad. You should return the partial derivatives of
%         the cost function with respect to Theta1 and Theta2 in Theta1_grad and
%         Theta2_grad, respectively. After implementing Part 2, you can check
%         that your implementation is correct by running checkNNGradients
%
%         Note: The vector y passed into the function is a vector of labels
%               containing values from 1..K. You need to map this vector into a
%               binary vector of 1's and 0's to be used with the neural network
%               cost function.
%
%         Hint: We recommend implementing backpropagation using a for-loop
%               over the training examples if you are implementing it for the
%               first time.
%
% Part 3: Implement regularization with the cost function and gradients.
%
%         Hint: You can implement this around the code for
%               backpropagation. That is, you can compute the gradients for
%               the regularization separately and then add them to Theta1_grad
%               and Theta2_grad from Part 2.
%

% recode y to Y
I = eye(num_labels);
Y = zeros(m, num_labels);
for i=1:m
  Y(i, :)= I(y(i), :);
end

% feedforward
a1 = [ones(m, 1) X];
z2 = a1*Theta1';
a2 = [ones(size(z2, 1), 1) sigmoid(z2)];
z3 = a2*Theta2';
a3 = sigmoid(z3);
h = a3;

% calculte penalty
p = sum(sum(Theta1(:, 2:end).^2, 2))+sum(sum(Theta2(:, 2:end).^2, 2));

% calculate J
J = sum(sum((-Y).*log(h) - (1-Y).*log(1-h), 2))/m + lambda*p/(2*m);

% calculate sigmas
sigma3 = a3.-Y;
sigma2 = (sigma3*Theta2).*sigmoidGradient([ones(size(z2, 1), 1) z2]);
sigma2 = sigma2(:, 2:end);

% accumulate gradients
delta1 = (a1'*sigma2);
delta2 = (a2'*sigma3);

% calculate regularized gradient
r1 = (lambda/m)*[zeros(size(Theta1, 1), 1) Theta1(:, 2:end)];
r2 = (lambda/m)*[zeros(size(Theta2, 1), 1) Theta2(:, 2:end)];
Theta1_grad = delta1'./m + r1;
Theta2_grad = delta2'./m + r2;

% -------------------------------------------------------------

% =========================================================================

% Unroll gradients
grad = [Theta1_grad(:) ; Theta2_grad(:)];


end