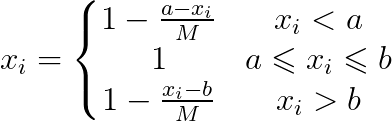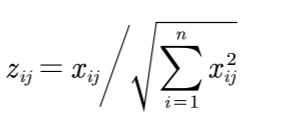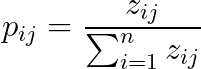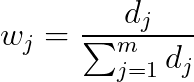基于熵权法的topsis分析（包含matlab源码以及实例）

            

目录

一、算法简述

         1.topsis分析法

         2.熵权法

         3.两种算法的结合

二、算法步骤

         1.判断指标类型

         2.数据正向化

         3.正向化矩阵标准化

         4.计算概率矩阵P

         5.计算各个指标的信息熵

         6.计算信息效用值

         7.计算熵权

         8.计算最优距离和最劣距离

         9.计算未归一化得分以及归一化得分

三、MATLAB代码实现

        1.主函数topsis.m

        2.正向化函数 Positivization.m

        3.熵权法函数 Entropy_Method.m

        4.ln函数 mylog.m

          写在前面

                 本篇不介绍熵权法以及topsis分析法的详细原理 若想了解请移步其他博客！！！

                恰恰相反，本篇为懒人福利，适用于数学建模等需要快速解决问题的赛事。

一、算法简述

       1.topsis分析法

            topsis算法是一种常见的综合评价办法，适用于有多个指标时的方案选择问题，如下图所示

            ps：以下数据为自行创造 仅用于讲解

方案\指标	可采矿量	基建投资	土地PH值	人员
方案1	5212	5000	5.7	45
方案2	3615	2600	4.0	32
方案3	5011	5412	5.0	43
方案4	4038	3200	4.3	38
方案5	4462	3600	4.8	40

            通过topsis分析法我们可以通过优劣分析，为五个方案分别赋予一个评分，显然评分越高，综合考量下来优势越大。

        2.熵权法

                我们已经知道topsis分析法可以给每个方案一个评分，但这个评分是在各个指标所占权重相同的前提下来算的，但我们遇到的问题大部分肯定有的指标重要，有的不那么重要，我们又不能去主观给他赋权重，这个问题应该怎么解决？没错，熵权法可以！

                熵权法是一种客观赋权方法，通过计算指标的信息熵，根据相对变化程度对整体的影响来决定指标权重。（不懂不要紧 会用就行）

        3.两种算法的结合

                了解了两种算法的基本原理，我们很容易想到，可以通过熵权法算出各指标的权重，进而通过topsis分析法进行评分，就能得到可信度较高的结果

二、算法步骤

        1.判断指标类型

                topsis模型一般是在所有指标均为极大型指标（数据越大越好）的基础上进行运算的，因此要判断各个指标都是什么类型，方便后面进行数据正向化。

                一般的常见类型有

                极大型（数据越大越好） 比如上方表格中的可采矿量

                极小型（数据越小越好）  比如上方表格中的基建投资

                中间型（数据稳定在某个固定的值最好） 比如上方表格里的ph最好保持在4.3

                区间型（数据在某个区间内最好）比如上方表格中的人员最好在[30,40]之间

         2.数据正向化

                极小型数据（PS：当数据不全为正数时 只能使用第二个公式）

                        

                  上面表格的基建投资为极小型数据 我们采用第二个公式来正向化

方案\基建投资	正向化前	正向化后
方案1	5000	412
方案2	2600	2812
方案3	5412	0
方案4	3200	2212
方案5	3600	1812

                中间型数据

                首先应该输入一个中间最优值再进行正向化

                        

                上面表格的土地PH值为中间型数据 我们的是4.3 

方案\土地PH	正向化前	正向化后
方案1	5.7	0
方案2	4.0	0.7857
方案3	5.0	0.5
方案4	4.3	1
方案5	4.8	0.6429

                区间型数据

                首先应该输入区间下限a和区间上限b再进行正向化

                          

                

                 上面表格的人员指标为区间型数据 我们的下限a是30 上限b是40  M是5

方案\人员	正向化前	正向化后
方案1	45	0
方案2	32	1
方案3	43	0.4
方案4	38	1
方案5	40	1

                正向化结束的矩阵称为正向化矩阵。如下表

方案\指标	可采矿量	基建投资	土地PH	人员
方案1	5212	412	0	0
方案2	3615	2812	0.7857	1
方案3	5011	0	0.5	0.4
方案4	4038	2212	1	1
方案5	4462	1812	0.6429	1

         3.正向化矩阵标准化

                正向矩阵标准化是为了消除不同量纲的影响。

                        

方案\指标	可采矿量	基建投资	土地PH	人员
方案1	0.5172	0.1022	0	0
方案2	0.3587	0.6975	0.5203	0.5625
方案3	0.4972	0	0.3311	0.2250
方案4	0.4007	0.5487	0.6622	0.5625
方案5	0.4428	0.4495	0.4257	0.5625

                这里得到的标准化矩阵要求所有数据必须全部大于等于0，如果有负数，需要按照以下方式重新进行标准化。

                

            PS:4-7步是熵权法确定指标权重的步骤 如果想实现各指标权重相同  默认是1/m

         4.计算概率矩阵P

                                 

方案\指标	可采矿量	基建投资	土地PH	人员
方案1	0.2333	0.0568	0	0
方案2	0.1618	0.3880	0.2683	0.2941
方案3	0.2243	0	0.1707	0.1176
方案4	0.1808	0.3052	0.3415	0.2941
方案5	0.1997	0.2500	0.2195	0.2941

         5.计算各个指标的信息熵

                        

                PS：由于概率矩阵中可能存在数值为0，但ln(0)为负无穷 我们这里将ln(0)设为0

指标	可采矿量	基建投资	土地PH	人员
信息熵	0.9945	0.7699	0.8416	0.8275

         6.计算信息效用值

                        

指标	可采矿量	基建投资	土地PH	人员
信息效用值	0.0055	0.2301	0.1584	0.1726

         7.计算熵权

                        

指标	可采矿量	基建投资	土地PH	人员
熵权	0.0098	0.4061	0.2795	0.3047

        8.计算最优距离和最劣距离

                定义最大值

指标	可采矿量	基建投资	土地PH	人员
	0.5172	0.6975	0.6622	0.5625

                定义最小值

   

指标	可采矿量	基建投资	土地PH	人员
	0.3587	0	0	0

                定义第i个（i=1,2, ... ,n）评价对象与最大值的距离

                        

                 定义第i个（i=1,2, ... ,n）评价对象与最小值的距离

                        

方案\距离
方案1	0.6024	0.0670
方案2	0.0766	0.6080
方案3	0.5127	0.2151
方案4	0.0955	0.5841
方案5	0.2017	0.4787

         9.计算未归一化得分以及归一化得分

                未归一化得分

                        

                归一化得分（分数相加等于1）

                        

方案\距离
方案1	0.1001	0.0352
方案2	0.8880	0.3120
方案3	0.2955	0.1038
方案4	0.8594	0.3019
方案5	0.7036	0.2472

                        由最终的可知，五个方案的的排名为5，1，4，2，3

三、MATLAB代码实现

        代码部分共有四个.m文件 一个主文件 三个函数

1.主函数topsis.m

[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象 共有' num2str(m) '个评价指标'])
judge=input(['这' num2str(m) '个指标是否需要正向化处理，需要请输入1 不需要请输入0：  ']);
if judge==1
    Position=input('请输入需要正向化处理的列 比如2，3，6列需要处理 则输入[2,3,6]：  ');
    disp('请输入这些列分别是什么指标类型（1：极小型 2：中间型 3：区间型）')
    Type=input('比如 2 3 6列分别是极小型 区间型 中间型 则输入[1,3,2]：  ');
    for i=1:size(Position,2)
        X(:,Position(i))=Positivization(X(:,Position(i)),Type(i),Position(i));
    end
    disp('正向化后的矩阵为 X=');
    disp(X);
end
%标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)



disp("请输入是否需要增加权重向量，需要输入1，不需要输入0")
Judge = input('请输入是否需要增加权重： ');
if Judge == 1
    if sum(sum(Z<0))>0
        disp('标准化矩阵中存在负数 正在重新标准化')
        for j=1:m
            minn=min(Z(:,j));
            maxx=max(Z(:,j));
            for i=1:n
                Z(i,j)=(Z(i,j)-minn)/(maxx-minn)
            end
        end
        disp('标准化完成 矩阵Z=  ');
        disp(Z);
    end
    W = Entropy_Method(Z);
    disp('熵权法确定的权重为：');
    disp(W);        
else
    W = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同，即都为1/m
end



D_P = sum([W .* (Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;%最优距离
D_N = sum([W .* (Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5;%最劣距离
S = D_N ./ (D_P+D_N);%相对接近度（可用来当得分）   
disp('最后的得分为：')
stand_S = S / sum(S)%得分归一化 最后各方案得分相加为1
[sorted_S,index] = sort(stand_S ,'descend');
disp('按得分从高到底排列方案 分别为:  ');
disp(index);%方案排名

2.正向化函数 Positivization.m

%正向化 Positivization 三个输入变量分别为目前处理的列向量 该列的指标类型 目前处理的是第几列
%输出变量为正向化后的列向量
function [posit_x]=Positivization(x,type,i)
    if type==1 %极小型
        posit_x=max(x)-x;
        %posit_x=1./x 如果该列数据全部大于0 也可以这样正向化
    elseif type==2%中间型
        best=input('请输入最佳的值:  ');
        M=max(abs(x-best));
        posit_x=1-abs(x-best)/M;
    elseif type==3%区间型
        a=input('请输入区间下限:  ');
        b=input('请输入区间上限:  ');
        MM=max(a-min(x),max(x)-b);
        posit_x = zeros(size(x,1),1);
        for i=1:size(x,1)
            if x(i)b
                posit_x(i)=1-(x(i)-b)/MM;
            else
                posit_x(i)=1;
            end
        end
    else 
        disp('请正确输入指标类型')
    end
end

3.熵权法函数 Entropy_Method.m

%计算权重
function [W] = Entropy_Method(Z)
    [n,m]=size(Z);
    d=zeros(1,m);
    for i=1:m
        x = Z(:,i);
        p = x./sum(x);%概率矩阵
        e = -sum(p .* mylog(p)) / mylog(n);%信息熵
        d(i)=1-e;%信息效用值
    end
    W=d./sum(d);%熵权
end

 4.ln函数 mylog.m

function [lnp] =  mylog(p)
n = length(p);   % 向量的长度
lnp = zeros(n,1);   % 初始化最后的结果
    for i = 1:n   % 开始循环
        if p(i) == 0   % 如果第i个元素为0
            lnp(i) = 0;  % 那么返回的第i个结果也为0
        else
            lnp(i) = log(p(i));  
        end
    end
end

注：本篇文章为自己系统了解后写下，不保证不会出现问题。大家如果对文章存在困惑或者质疑 ，欢迎在评论区留言。

参考链接

熵值法与TOPSIS法以及两者结合 作者：卖山楂啦prss

数学建模之熵权法——基于Topsis模型 作者：我本无忧

基于熵权法的Topsis模型（清风数学建模课后笔记） 作者：weixin_57449924