多元线性回归模型的各种诊断
多元线性回归模型的各种诊断
-
- 例一 强影响点诊断
- 例二 异方差性诊断
- 例三 自相关性诊断
- 例四 多重共线性诊断
提示:
①这里没有原理,只有R的代码、运行结果以及对部分结果的解读!!!
②有重复的部分,节约时间的话可以重点看标黄的地方.
例一 强影响点诊断
学生化残差:

绘制残差图:


从残差图中可以看出,大部分数据位于两倍标准差内. 残差有递减的趋势,因而随机误差项的齐性假设可能不太合理.
绘制回归诊断图:
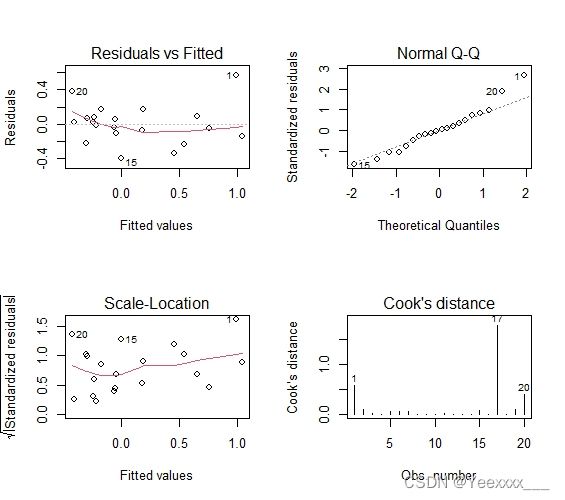
Residuals vs Fitted:残差与估计值之间的关系,数据点应该大致落在两倍标准差也就是2、-2之间,且这些点不应该呈现任何有规律的趋势.
Normal QQ:若满足正态假设,那么图上的点应该落在呈45度角的直线上;若不是如此,那么就违反了正态性的假设.
Scale-Location:GM假设中的同方差可以通过这张图诊断,方差应该呈现基本确定或持平的样子.
Cook’s distance:Cook距离,用于强影响点的诊断.
影响分析:
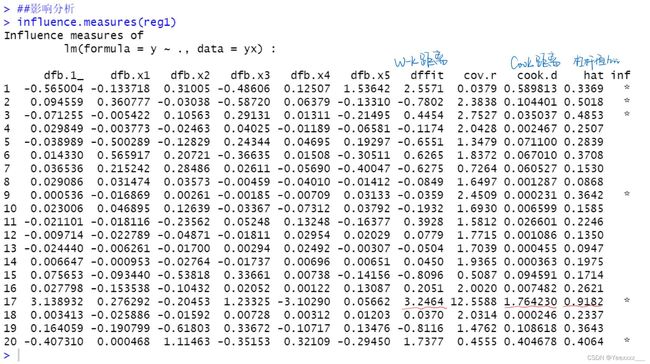
17号点的各种影响度量都很大,所以认为17号数据点是强影响点. 使用car包的influencePlot()函数,找出影响回归的异常点和强影响点.
图中圆很大的点可能是对模型参数的估计造成的较强影响的强影响点.
code:
yx=read.table("eg5.6_ch5.txt",header=T)
yx
reg1=lm(y~.,data=yx)
summary(reg1)
sse = 0.2618**2*14
r2 =0.8104
sst = sse/(1-r2)
Ft = 11.97
ssr = sst - sse;ssr
(ssr/5)/(sse/14)
##学生化残差
rstandard(reg1) # 学生化内残差
0.562611/(0.2618*sqrt(1-0.3369))
rstudent(reg1) # 学生化外残差
##残差图
ri=rstandard(reg1)
yhat=predict(reg1);yhat # y的估计
plot(ri~yhat)
abline(h=0,col="red",lty="dashed")
abline(h=2,col="blue",lty="dashed")
##残差诊断图4张
op<-par(mfrow=c(2,2)) # 2*2子图
plot(reg1,1:4)
par(op)
##影响分析
influence.measures(reg1)
library(car)
influencePlot(reg1,main="Influence Plot",sub="Circle size is proportional to Cook's distance")
例二 异方差性诊断
绘制残差图:

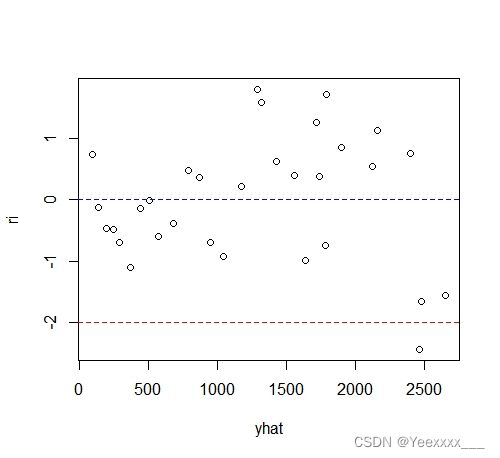
从图中可以看出,从左到右各个点逐渐散开,说明误差项具有异方差性.
等级相关系数法检验异方差性:

H 0 : r s = 0 H_0:r_s=0 H0:rs=0 (同方差), H 1 : r s ≠ 0 H_1:r_s\neq0 H1:rs=0 (异方差). 所以在0.05的显著性水平下,p值 0.001301 < 0.05 0.001301 < 0.05 0.001301<0.05,拒绝原假设,说明随机误差项存在异方差性.
p值和显著性水平 α \alpha α比较,和等级相关系数法一样.
GQ检验:

White检验:

通过加权最小二乘修正异方差:
(anova方差分析)

修正异方差性后模型的结果更加精确.
code:
saving=read.table("eg5.8_ch5.txt",header=T)
reg2=lm(y~x,data=saving)
summary(reg2)
plot(y~x,data=saving,col="red")
abline(reg2,col="blue")
##残差图
ri=rstandard(reg2)
yhat=predict(reg2)
plot(ri~yhat)
abline(h=0,col="blue",lty="dashed")
abline(h=-2,col="red",lty="dashed")
##spearman test
abe=abs(reg2$residual)
cor.test(~abe+x,data=saving,method="spearman")
##BP test
#检验结果
library(lmtest)
library(zoo)
bptest(reg2,studentize=FALSE)
bptest(reg2) #学生化具有修正异方差的作用
#辅助回归结果
e=residuals(reg2)
e2=(reg2$residuals)^2;
lmre=lm(e2~saving$x)
summary(lmre)
LM=31*0.2723; LM
##GQ test(lmtest包)
gqtest(reg2)
##white test(whitestrap包)
#检验结果
# install.packages('whitestrap')
library(whitestrap)
white_test(reg2)
#辅助回归结果
x=saving$x
lmre2=lm(e2~x+I(x^2))
summary(lmre2)
white=31*0.2974; white
##加权最小二乘
regw=lm(y~x,data=saving,weight=x^(-1/2))
anova(regw)
summary(regw)
例三 自相关性诊断
(和例二是同一份数据)
DW检验: 记得看适用条件!!!

DW=1.2529,R不会直接给对应的上下限,所以需要自己查DW分布表中的上下限,与DW比较. 或者看p值,p-value=0.008674与显著性水平 α \alpha α比较,若 p < α p<\alpha p<α拒绝原假设,认为存在一阶自相关性.
自相关系数的估计值为0.37355,说明误差项存在中度自相关.
拉格朗日乘数检验:order是需要检验的阶数

显著性水平 α = 0.05 \alpha =0.05 α=0.05
o r d e r = 1 order=1 order=1时, p − v a l u e = 0.0546 p-value=0.0546 p−value=0.0546,因为 p > α p > \alpha p>α,不能拒绝原假设,认为这个模型不存在显著的一阶自相关.
o r d e r = 5 order=5 order=5时, p − v a l u e = 0.03772 p-value=0.03772 p−value=0.03772,因为 p < α p < \alpha p<α,拒绝原假设,认为这个模型存在显著的五阶自相关.
通过科克伦-奥克特迭代法消除自相关性:只适用于二阶及以上的高阶自相关

code:
saving=read.table("eg5.8_ch5.txt",header=T)
reg2=lm(y~x,data=saving)
##DW检验(lmtest包)
dwtest(reg2)
rho=1-0.5* 1.2529; rho # DW = 2(1-rho自相关系数)
##拉格朗日乘数检验
bgtest(reg2,order=1)
bgtest(reg2,order=5)
##广义差分
n=nrow(saving)
st=saving[-1,]
stlag1=saving[1:(n-1),]
sn=st-rho*stlag1 # DW
cbind(st,stlag1,sn) # 二三列滞后一期 最后两列广义差分
reg3=lm(y~x,data=sn)
summary(reg3)
##科克伦-奥克特法
# install.packages("orcutt")
library(orcutt)
cochrane.orcutt(reg2)
例四 多重共线性诊断
从相关系数矩阵中可以看出解释变量中至少存在两组显著的负线性相关.
回归诊断:
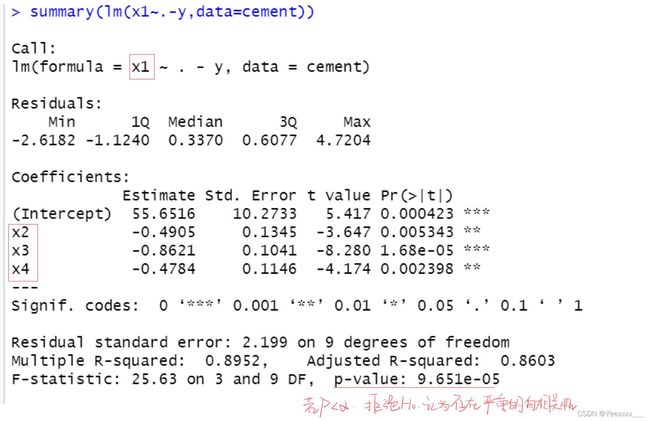
这里只做了 x 1 x_1 x1与其余解释变量的辅助回归方程,其他可以自己试.
方差膨胀因子诊断:

判断方法一:一般方差膨胀因子大于10,认为存在严重的多重共线性. 所以上述结果说明存在两组严重的多重共线性.
判断方法二:四个vif的平均值大于1,说明存在严重的多重共线性.
特征根与条件数诊断法:

至少存在一个特征根近似为0时,则解释变量之间必存在多重共线性.
条件数大于100时认为存在严重的多重共线性.
code:
cement=read.table("eg5.10_ch5.txt",header=T)
reg4=lm(y~.,data=cement)
summary(reg4)
cor(cement)
summary(lm(x1~.-y,data=cement))
##VIF
# install.packages('DAAG')
library(DAAG)
vif(reg4,digit=3)
##特征根和条件数
xx=as.matrix(cbind(1,cement[,1:4]))
pho=cor(t(xx)%*%(xx)); pho
eigen(pho)
kappa(pho,exact=TRUE)









