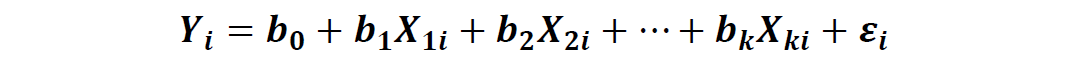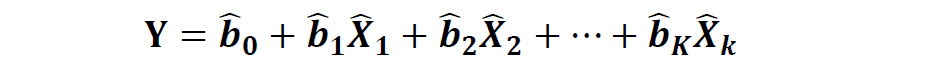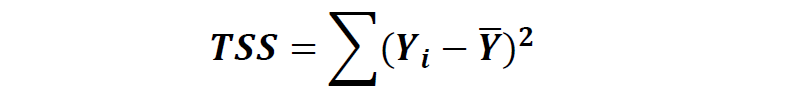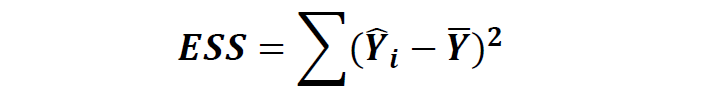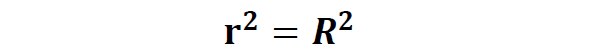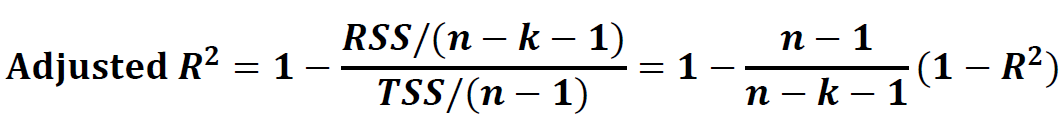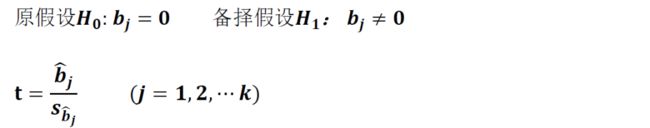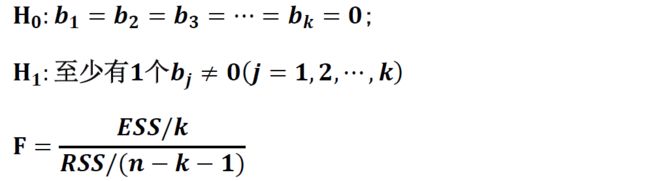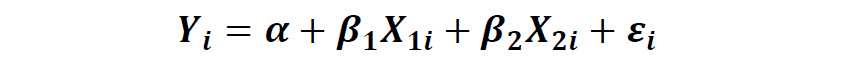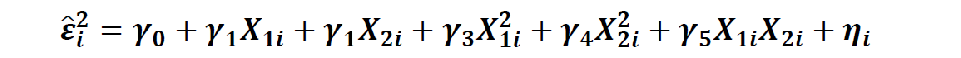多元线性回归matlab代码例题_多元线性回归与模型诊断
一、多元线性回归
1.多元线性回归的基本表达式
在多元线性回归中会有多个解释变量：
预测解释变量的估计方程如下：
注：额外的假设条件
①解释变量之间不能存在太强的线性相关关系(一般ρ<0.7)
②其他条件与一元线性回归类似。
2.回归方程的模型拟合度
在进行回归模型之前，我们可以计算总的波动误差如下：
在运用回归模型后，总误差可以分解为以下两种：
1)不能解释变量误差(误差项的平方)
2)被回归方程可以解释的误差
根据以上解释我们可以整理出以下方差分析表：
df自由度 |
SS |
MSS(方差) |
|
Explained可以解释的误差 |
k |
ESS |
ESS/k |
Residual 误差项 |
n-k-1 |
RSS |
RSS/(n-k-1) |
Total 总误差 |
n-1 |
TSS |
3)拟合判定系数R方
注：一元线性回归的R方比较特殊，为相关系数的平方：
通常情况下R方越大，说明模型拟合的解释力度越好，但有时通过不断增加解释变量可以相应提高R方，这时候拟合效果并不一定是最好，所以提出以下修正R方来进行判断：
3.回归方程的推论
①置信区间(同一元线性回归类似)
②假设检验(同一元线性回归类似)
③联合假设检验
通常F检验被用于检测多元线性回归的解释变量斜率是否同时等于0：
判断准则：如果F(T检验计算值)>F(关键值)，则拒绝原假设H0.
Python案例分析：
#导入cv模块import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltimport pandas as pddata=pd.read_excel('D:/欧晨的金学智库/线性回归案例.xlsx',header=0,index_col=0)data.head()
#多元线性回归import statsmodels.api as sm model3 = sm.OLS(data['weight'],sm.add_constant(data[['age','height']]))result = model3.fit()result.summary() print(result.summary())
分析:经过调整的R方=0.639，拟合系数一般，并不是特别好。
F统计量=26.67(检验解释变量系数是否全为0？)，P-value=4.05*10-7，非常小，拒绝原假设；
常数项估计-140.762，P值很小，说明截距项显著，不为0；
age项估计-0.0485，P值较大>0.05，说明age项不显著，可以尝试剔除该解释变量；
height项1.1973，P值很小，说明height项显著，不为0。
二、模型诊断
1.自变量选择偏差的权衡
(1)丢失重要变量
剩余变量吸收了丢失的重要变量的信息，即用剩余变量进行了过度拟合；
过于高估残差项(包含真实残差项的信息、忽略重要变量的信息)
(2)加入无关变量
变量系数的估计偏差(大样本，无关变量会收敛于0)
增加了模型参数估计的不确定性
增加了R方的值，但是使得调整的R方减小
(3)两种合理估计线性回归系数的方法
①一般情况模型变量的选择方法
a.将所有变量加入进行回归；
b.移除拟合效果最差的一个变量(尤其是不显著的变量)；
c.移除后继续采用线性回归模型进行拟合，再次移除不显著的变量；
d.重复以上步骤，直至所有变量的拟合结果都显著；
注：通常选择显著性α在1%~0.1%(相应t值至少为2.57或3.29)Python案例分析：在上述案例中，我们得到age项不显著，可以剔除该解释变量，只用height进行线性回归：
#载入OLS回归库import statsmodels.api as sm model1 = sm.OLS(data['weight'], sm.add_constant(data['height']))result = model1.fit()result.summary() print(result.summary())
分析：经过调整的R方=0.652>0.639，说明剔除age变量后，拟合效果更好。剩余的截距项和身高的P值均很小，说明显著不为0，所以应当保留。
②K折交叉检验
a.确定模型数量(有n个解释变量——每个变量选择有或无，通常有2^n个模型)
b.将数据分成相等数量的k个集合，其中k-1个集合作为训练集拟合回归方程，剩下的1个集合作为验证集；重复进行交叉拟合验证(总计有k次)。
c.每个模型都采用b的方式进行验证。
d.计算每个模型的总的残差项(验证k次)的和，选择残差项和或其均值最小的一组模型最为最优模型。
Python案例分析：依旧使用以上案例，有2个解释变量，所以应当有2^2=4个模型，我们排除解释变量均为0的情况，来做3个模型的K折交叉检验：
y=data.weightX1=data[['age','height']]from sklearn.linear_model import LinearRegression #载入机器学习中线性回归包lm = LinearRegression()from sklearn.model_selection import cross_val_score #载入机器学习中交叉检验包scores1 = cross_val_score(lm, X1, y, cv=10) #cv=10，数据分成10等均匀份print (scores1)
分析：上面的scores都是负数，为什么均方误差会出现负数的情况呢？因为这里的mean_squared_error是一种损失函数，优化的目标的使其最小化，而分类准确率是一种奖励函数，优化的目标是使其最大化，因而选择只用height做变量。
print('用age,height做自变量：',np.sqrt(-scores1.mean()))np.sqrt(-scores1.mean())X2=data[['age']]scores2 = cross_val_score(lm, X2, y, cv=10)print('只用age做自变量：',np.sqrt(-scores2.mean()))X3=data[['height']]scores3 = cross_val_score(lm, X3, y, cv=10)print('只用height做自变量：',np.sqrt(-scores3.mean()))lm.fit(X3,y)
print('intercept_:%.3f' % lm.intercept_)print('coef_:%.3f' % lm.coef_)
2.残差的异方差性
如果残差项的方差恒定不变(即为常数)，则通常认定为同方差性，反之如果方差一直在变动并未恒定则认定为有异方差性。
注：如果存在异方差性进行线性回归，则回归系数的假设检验以及置信区间的估计通常是有偏差的。
采用怀特检验法来验证异方差性：
例如检验有2个自变量的线性回归方程：
注：残差项的方程的检验统计量的解释力度记为nR2(即第②步中计算)，其检验分布为卡方分布(自由度为——k(k+3)/2)
Python案例分析：依旧以weight~age+height为例
import statsmodels.api as sm model3 = sm.OLS(data['weight'],sm.add_constant(data[['age','height']]))result3 = model3.fit()sm.stats.diagnostic.het_white(result3.resid, exog = result3.model.exog)
分析：
第一个为：LM统计量值
第二个为：响应的p值，0.53远大于显著性水平0.05，因此接受原假设，即残差方差是一个常数
第三个为：F统计量值，用来检验残差平方项与自变量之间是否独立，如果独立则表明残差方差齐性
第四个为：F统计量对应的p值，也是远大于0.05的，因此进一步验证了残差方差的齐性。
3.多重共线性
①完美多重共线性自变量之间存在相关系数=1的情况，即一个自变量可以被另一个自变量完全解释，完全替代。
② 一般的多重共线性- 一个自变量或多个自变量之间可以大部分相互解释，存在较高的相关性
当数据存在多重共线性时，通常发现系数之间有较强的显著关系，删除t统计量较小的(如t<1.96)
4.绘制残差图与异常值
残差图即自变量与残差之间的散点图，异常值即偏离正常中心值较大的奇异点。
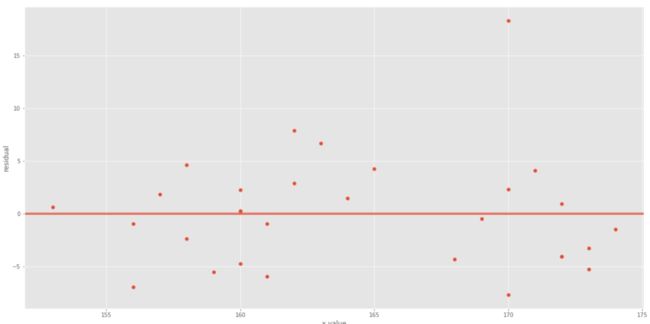
我们以上节一元线性回归的案例的身高与体重的回归结果残差图为例：
很明显上图中对应x在170的时候存在异常值。
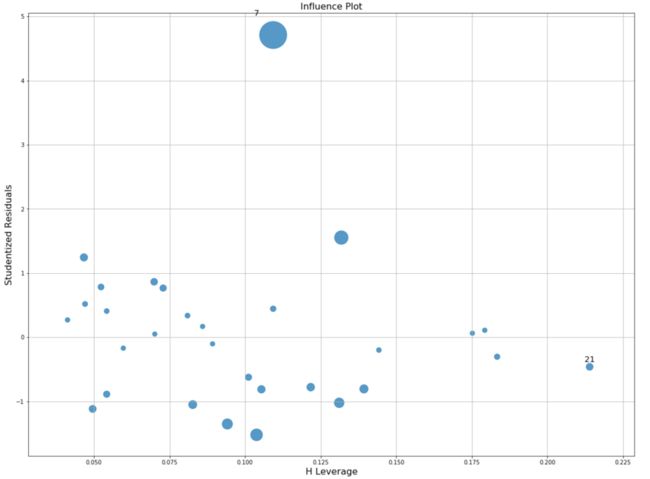
异常值的判断：库克距离(Cook’sdistance)
Python案例分析：
#异常值的检验#使用Cook距离描绘这个模型的影响图：import statsmodels.api as sm model3 = sm.OLS(data['weight'],sm.add_constant(data[['age','height']]))result3 = model3.fit()fig, ax = plt.subplots(figsize=(19.2, 14.4))fig = sm.graphics.influence_plot(result3, ax=ax, criterion="cooks")plt.grid()
分析：由上图可以得到，第7个数据是偏离较远的，气泡很大。
真实数据如下：
