2012 Multi-University Training Contest 2

看完了第一道题，感觉贪心可做，然后跟cz说了一下，他去写，然后我去看另外一道题，就这样悲剧开始了，被坑了一下午，看了一道自认为不算太难的题，然后自己写写，试了点数据感觉不怎么对，然后删了重新想，一直就在纠结，中间交流了一下其他题，在我试图暴力第二道题失败后继续思考那道题，就这样思考到了最后1个小时果断放弃去交流其他题了。最后貌似那道题只有11个队过了。。赛后看了下题解：较难的动态规划题、、、Orz。。

1001 Hero 

代码：

 

View Code 

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5  using  namespace std;
 6  struct hero
 7 {
 8      double v;
 9      int hp;
10      int dp;    
11 }p[ 21];
12  int comp( const  void *a, const  void *b)
13 {
14      return (*( struct hero *)a).v<(*( struct hero *)b).v? 1:- 1;
15 }
16  int main()
17 {
18      int n,i,j,sum;
19      while(~scanf( " %d ",&n))
20     {
21         sum= 0;
22          for(i= 0;i<n;i++)
23         {
24             scanf( " %d%d ",&p[i].dp,&p[i].hp);
25             p[i].v=p[i].dp* 1.0/p[i].hp;
26         }
27         qsort(p,n, sizeof(p[ 0]),comp);
28          for(i= 0;i<n;i++)
29              for(j=i;j<n;j++)
30                 sum+=(p[j].dp*p[i].hp);
31         printf( " %d\n ",sum);
32     }
33      return  0;
34 }
35

1002 Meeting point-1 

比赛的时候我的想法，按横坐标排序，找到中位数，前后枚举300个点，然后算出最小的，虽然这种方法没有理论依据，但却是非常简单的做法。

代码：

View Code 

 1 #include <iostream>
 2 #include <cstring>
 3 #include <cstdlib>
 4 #include <cstdio>
 5  #define N 100010
 6  using  namespace std;
 7  struct point
 8 {
 9      long  long x;
10      long  long y;
11 }a[N];
12  long  long Abs( long  long x)
13 {
14      return x>= 0?x:-x;
15 }
16  int comp( const  void *a, const  void *b)
17 {
18      struct point *c=( struct point *)a;
19      struct point *d=( struct point *)b;
20      if(c->x!=d->x)
21          return c->x-d->x;
22      else
23          return d->y-c->y;
24 }
25  long  long work( int k, int n)
26 {
27      int i;
28      long  long sum= 0;
29      for(i= 0;i<n;i++)
30     {
31         sum+=Abs(a[k].x-a[i].x);
32         sum+=Abs(a[k].y-a[i].y);
33     }
34      return sum;
35 }
36  int main()
37 {
38      int t,n,u,d,i;
39      long  long min,s;
40     scanf( " %d ",&t);
41      while(t--)
42     {
43         scanf( " %d ",&n);
44          for(i= 0;i<n;i++)
45         {
46             scanf( " %I64d%I64d ",&a[i].x,&a[i].y);
47         }
48         qsort(a,n, sizeof(a[ 0]),comp);
49         d=n/ 2- 300;
50         u=n/ 2+ 300;
51          if(d< 0)
52             d= 0;
53          if(u>n- 1)
54             u=n- 1;
55         min= 1;
56         min<<= 60;
57          for(i=d;i<=u;i++)
58         {
59             s=work(i,n);
60              if(min>s)
61                 min=s;
62         }
63         printf( " %I64d\n ",min);
64     }
65      return  0;
66

 

 

1003  Meeting point-2 

跟上一个一样，找中位数，枚举，枚举250个点就够了。弱菜只会这么水而且无技术含量的SB方法。。

代码： 

View Code 

 1 #include <iostream>
 2 #include <cstring>
 3 #include <cstdlib>
 4 #include <cstdio>
 5  #define N 100010
 6  using  namespace std;
 7  struct point
 8 {
 9      long  long x;
10      long  long y;
11 }a[N];
12  int Abs( int x)
13 {
14      return x>= 0?x:-x;
15 }
16  int comp( const  void *a, const  void *b)
17 {
18      struct point *c=( struct point *)a;
19      struct point *d=( struct point *)b;
20      if(c->x!=d->x)
21          return c->x-d->x;
22      else
23          return d->y-c->y;
24 }
25  long  long work( int k, int n)
26 {
27      int i;
28      long  long sum= 0;
29      for(i= 0;i<n;i++)
30     {
31         sum+=Abs(a[k].x-a[i].x)>Abs(a[k].y-a[i].y)?Abs(a[k].x-a[i].x):Abs(a[k].y-a[i].y);
32     }
33      return sum;
34 }
35  int main()
36 {
37      int t,n,u,d,i;
38      long  long min,s;
39     scanf( " %d ",&t);
40      while(t--)
41     {
42         scanf( " %d ",&n);
43          for(i= 0;i<n;i++)
44         {
45             scanf( " %I64d%I64d ",&a[i].x,&a[i].y);
46         }
47         qsort(a,n, sizeof(a[ 0]),comp);
48         d=n/ 2- 250;
49         u=n/ 2+ 250;
50          if(d< 0)
51             d= 0;
52          if(u>n- 1)
53             u=n- 1;
54         min= 1;
55         min<<= 60;
56          for(i=d;i<=u;i++)
57         {
58             s=work(i,n);
59              if(min>s)
60                 min=s;
61         }
62         printf( " %I64d\n ",min);
63     }
64      return  0;
65 }
66

 

 

1004 Matrix

思路：先按照权值从大到小排序，再利用并查集判断是不是和不能到达的点联通，类似kruskal最小生成树的算法。

代码：

View Code 

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5  using  namespace std;
 6  const  int N= 100001;
 7  int map[N],vis[N];
 8  int n,k;
 9  struct Map
10 {
11      int u;
12      int v;
13      int value;
14 }edge[N];
15  int comp( const  void *a, const  void *b)
16 {
17       return (*( struct Map *)a).value<(*( struct Map *)b).value? 1:- 1;
18 }
19  int find( int x)
20 {
21      int r=x;
22      while(map[r]!=r)
23         r=map[r];
24      return r;
25 }
26  void merge()
27 {
28     __int64 sum= 0;
29      int i;
30      for(i= 0;i<n- 1;i++)
31     {        
32          int fx=find(edge[i].u);
33          int fy=find(edge[i].v);
34          if(vis[fy]== 0)
35             map[fy]=fx;
36          else  if(vis[fx]== 0)
37             map[fx]=fy;
38          else
39             sum+=edge[i].value;
40     }
41     printf( " %I64d\n ",sum);
42 }
43  int main()
44 {
45      int t,i,a;
46     scanf( " %d ",&t);
47      while(t--)
48     {
49         scanf( " %d%d ",&n,&k);
50          for(i= 0;i<N;i++)
51             map[i]=i;
52         memset(vis, 0, sizeof(vis));
53          for(i= 0;i<n- 1;i++)
54         {
55             scanf( " %d%d%d ",&edge[i].u,&edge[i].v,&edge[i].value);
56         }
57          for(i= 0;i<k;i++)
58         {
59             scanf( " %d ",&a);
60             vis[a]= 1;
61         }
62         qsort(edge,n- 1, sizeof(edge[ 0]),comp);
63         merge();
64     }
65      return  0;
66 }
67

 

 

 

 

 

 

 

 

 

 

附：

官方题解：

 

1001 Hero

 

中等偏易题，状态压缩dp，用dp[mask]表示杀死mask集合的敌人时，这些敌人造成的最小hp消耗。有转移方程dp[mask] = min{dp[mask - {i}] + hp_sum[mask] * dps[i], for all i in mask}

 

1002    Meeting point-1:

 

平面上两点间的 Manhattan 距离为 |x1-x2| + |y1-y2|

X 方向的距离与 Y 方向上的距离可以分开来处理。假设我们以 (xi,yi) 作为开会的地点，那么其余的点到该开会地点所需的时间为 X 方向上到 xi 所需要的时间加上 Y 方向上到 yi 所需要的时间。

对数据预处理后可以快速地求出x坐标小于xi的点的个数rankx, 并且这些 x 坐标值之和 sumx，那么这些点 X 方向上对结果的贡献为 rankx * xi - sumx；同理可以处理出 x 坐标大于 xi 的点在 X 方向上对结果的贡献值。同理可求得其余点在 Y 方向上到达 yi 所需要的总时间。

 

1003   Meeting point-2:

 

平面上两点间的 Chebyshev距离为 max(|x1-x2|, |y1-y2|)

                        

 

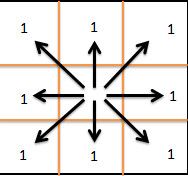
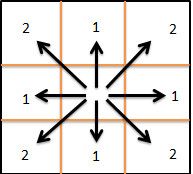
          Chebyshev                                               Manhattan

对于原坐标系中两点间的 Chebyshev 距离，是将坐标轴顺时针旋转45度并将所有点的坐标值放大sqrt(2)倍所得到的新坐标系中的Manhattan距离的二分之一。

大家可以画图想一下……

假设有两点(x1,y1), (x2,y2)，不妨设 x1>x2（否则交换这两点即可）。

则Chebyshev距离 D1 = max(|x1-x2|, |y1-y2|)

这两点个对应到新坐标系中的坐标为 (x1-y1, x1+y1), (x2-y2, x2+y2)

则Manhattan 距离D2 = |x1-y1-x2+y2| + |x1+y1-x2-y2|

分四种情况讨论：

1.1　y1>y2 && x1-x2>y1-y2

D1 = max(x1-x2, y1-y2) = x1 - x2

D2 = x1-y1-x2+y2 + x1+y1-x2-y2 = 2(x1-x2)

1.2   y1>y2 && x1-x2<=y1-y2

D1 = max(x1-x2,y1-y2) = y1-y2

D2 = -(x1-y1-x2+y2) + x1+y1-x2-y2 = 2(y1-y2)

2.1   y1<=y2 && x1-x2>y2-y1

D1 = max(x1-x2, y2-y1) = x1-x2

D2 = x1-y1-x2+y2 + x1+y1-x2-y2 = 2(x1-x2)

2.2   y1<=y2 && x1-x2<=y2-y1

D1 = max(x1-x2, y2-y1) = y2-y1

D2 = x1-y1-x2+y2 - (x1+y1-x2-y2) = 2(y2-y1)

所以先将Chebyshev距离形式转化成Manhattan距离的形式再求解，求解过程参考 Meeting point-2

 

1004  Matrix:(cin,cout标程要运行2s，scanf，printf 1s)

 

对于有n个结点的树，容易证明删除任意的k (k<=n-1)条边都能将原树切成k+1个部分。按照题意至少需要将原树划分成d个部分（此时每部分中都包含一个危险的点），删除的边数为d-1。

贪心算法：类似kruskal最小生成树的过程，不过此处将边按权值从大到小排列，每次将边加进来时要判断是否会使两个危险的点连通，是的话这条边就是需要被删除的，否则将它加到树上。

树形dp：以任意一个点作为根生成树，对于每个结点保存两个值

dp[u][0]: 与u连通的子孙结点中没有危险结点时需要删除的最小边权值，若u为危险结点，则该值为无穷大。

dp[u][1]：与u连通的子孙结点中没有危险结点时需要删除的最小边权值。

递推方程：

一、u为叶子结点

(1) u 是危险点

dp[u][0] = inf, dp[u][1] = 0;

(2) u不是危险点

dp[u][0] = 0, dp[u][1] = 0;

二、U不是叶子结点

(1)      u是危险点

Dp[u][0] = inf,

(2)      u不是危险点

 

1005     Save the Dwarf

 

较难的动态规划题。一个重要的观察是，如果某些矮人可以逃脱，那么我们总可以把他们的逃脱顺序按照Ai+Bi递增排序（即Ai+Bi最小的先逃脱），得到的结果不会更坏。于是可以先按Ai+Bi排序处理即可。用dp[i][j]表示最后i个人能逃出j个时，需要之前井中剩下的人的最小A高度之和。有如下转移方程dp[i][j] = min(dp[i-1][j] - s[i-1].a, max(dp[i-1][j-1], H - sumA[i-1] - s[i-1].b ))。最后找到最大的j满足dp[n][j]<=0即为所求。

 p.s. 似乎也可以用贪心来做，但是证明比较复杂。

 

1006    Climb the Hill

 

中等博弈题。此题的简化版本是不考虑King的存在，双方一直走到不能走的一方为负。此时的解法是根据人数的奇偶性：把人从上顶向下的位置记为a1,a2,...an, 如果为偶数个人，则把a(2i-1)和a(2i)之间的距离当做一个Nim堆，变成一共n/2堆的Nim游戏；如果为奇数个人，则把山顶到a1的距离当做一个Nim堆，a(i*2)到a(i*2+1)的距离当做Nim堆，一共(n+1)/2堆。

考虑King的情况和上述版本几乎一致，只要把King当作普通人一样处理即可。除了两种特殊情况：1. 当King是第一个人时，Alice直接胜 2. 当King是第二个人且一共有奇数个人时，第一堆的大小需要减1。

 

1007  Mission Impossible:

 

题目模型可以抽象为：有三个点光源，一个放在z = 0 平面的凸多面体，求三个点光源照射凸多面体在z = 0平面上的影子的公共部分。

对于每个点光源，它在z = 0平面上产生的影子都是一个凸多边形，三个凸多边形的交集即为所求。

凸多边形求法：每个点光源和凸多面体的每个点进行连线，和z = 0平面求交点，对于交点求凸包，即为所求凸多边形。

三个凸多边形求交集：半平面交

 

1008    Nim

 

中等难度状态压缩dp题。要注意的是直觉得出的一些贪心算法往往是有反例的。基本思路是从高到低计算（从低到高也可以），用状态dp[k][mask]表示高k位如果要满足要求，并且集合mask中的数需要从低位进位时，最少需要加多少石子。

 

1009   Power transmission

 

题目大意可大致表述为从节点s向节点t传送电力，电力在传送过程中会有所消耗，不同节点之间，电力传送消耗的值有所不同。要求选择一条

使得电力消耗最小的线路。如果不能把电力从s点传送到t点，或者电力损失殆尽，则输出IMPOSSIBLE！

如果从s出发，没有到达t的路径，则输出IMPOSSIBLE！

如果存在这样一条路径p = (s,p1,p2,p3,...,pn,t),那么最后到达t的电力为M*(1-b1%)*(1-b2%)*...*(1-bn%)*(1-bn+1%)。即我们需要找到这样一条路径，使得(1-b1%)*(1-b2%)*...*(1-bn%)*(1-bn+1%)最大。

解题思路1：

我们可以把乘积的形式通过取对数化作连续相加的形式

即log(1-b1%) +…+log(1-bn+1%),由于 log(1-bi%)都是小于0的，我们要求这个式子的最大值就是求每个子式取绝对值的最小值。所以通过取对数在取绝对值的操作，我们可以得到两节点之间新的边权。同时题目也转化为求单源最短路问题。最后注意把结果进行转化。

解题思路2：

直接贪心。类似于Dijkstra算法。我们要求损耗最小，也就是剩余最大。对于每个节点，我们记录起当前可以达到的剩余最大电力。和Dijkstra算法相似，我们这里每次找寻的是尚未标记的拥有最大值的结点，并把这个最大值作为当前结点的最终结果，标记此结点并通过当前结点拓展与之相连的结点。因为从一个结点传输电力到另一个几点，电力的总量是不会增加的。所以，在以后的贪心过程中，不会更新之前已经标记的结点，因为不可能有更大的值。

这样只要求得最后到达t的最大剩余电力就能得出答案。

 

1010   Maximum Subsequences

 

难题。用分治法来做，关键在于O(n)时间完成合并操作。我们把要求的结果开方，答案不变，即求max{abs(a[i]+...+a[j]) / (j-i+1)}. 设函数f(x,y) = |y| / sqrt(x)，则x即为子序列长度，y即为子序列和，下面我们可以把(x,y)看作平面内的点。

欲处理a[i..j]之内的最优区间，递归处理a[i..mid]和a[(mid+1)...j]，然后设

b1 = (1, a_mid), b2 = (2, a_mid + a_(mid-1)), b3 = (3, a_mid + a_(mid-1) + a_(mid-2))...

c1 = (1, a_(mid+1)), c2 = (2, a_(mid+1)+a_(mid+2)) ...

我们把bi, ci都看作二维平面内的点，分别计算出bi, ci的上凸包和下凸包，再把两个上凸包合并，两个下凸包合并，最优解一定在合并得到的凸包上。这个过程是可以O(n)完成的。

两个上凸包p,q合并成t是指如下过程：

t1 = p1 + q1

如果ti = pj + qk, 那么t(i+1) = p(j+1) + qk 或 t(i+1) = pj + q(k+1)，根据凸性决定保留哪一个

下凸包的合并也是类似过程。