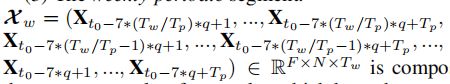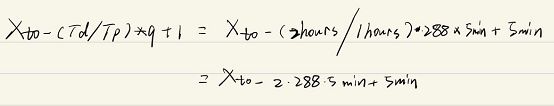(ASTGCN)Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting

ASTGCN：注意力机制的时空图卷积神经网络，来预测高速公路上的车流

由于在学习这方面的知识，就把自己的学习笔记写下来，方便以后自己复习

文章定义的概念如下：G = (V, E, A)，V是有限节点的集合，E是边集合，A是N*N的邻接矩阵

文章中有一句话是

Suppose the f -th time series recorded on each node in the

traffific network G is the traffific flflow sequence,

我的理解刚开始是，说每个节点都包含了f个时间序列的数据，看到后面的公式，其实不是，每个节点在当前时刻其实只有不同的属性值，是个实数:R，F代表的是特征的个数，有几个特征：比如：speed，occur.........

是在时间t的第i个节点的所有特征信息。

是在时间t的第i个节点的第c个特征，是个标量，实数

 是t时刻所有N个节点的所有节点的特征信息

是过去tau个时刻所有节点的所有特征信息

 文章要解决的问题是输入得到

下个时间窗Tp的预测车流，

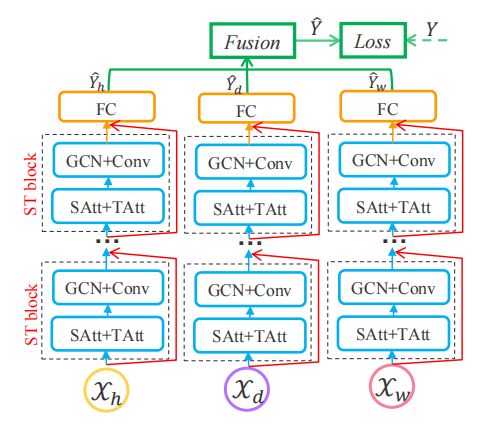
文章提出的模型结构如下:

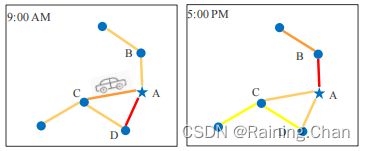
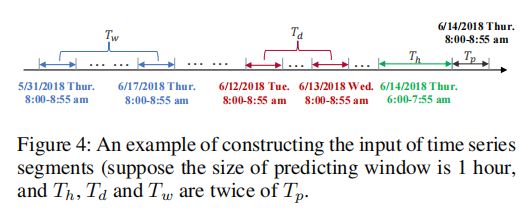
简单来说就是分了三种不同的时间间隔，分别是：用最近的两小时预测今天的下一小时(recent)，用昨天，前天，大前天的这一时刻的两小时预测今天这一小时(daily-peridodic)，用上周，上上周，上上上周的这一天的这一时刻的两小时预测今天这一小时(weekly-periodic)。

文中的定义如下:

这是recent的

这是daily的

这是weekly的

定义中发现有个q是什么意思呢？

假设每天采样q次。

以文章举的例子来说:

 Th=Tw=Td=2Tp=2 hours，而且文中哪个地方好像说了，它用的这个数据集是每五分钟融合一次数据，这里不难看出q=24 hours / 5mins =288，那么每天就采样288次。

比方说这个式子:带入计算：

 这里的单位就是一个采样间隔:5min

然后就是空间和时间的注意力模块:

这里我按照他给出的定义算了一遍:S的形状是N*N的，并且这里有个定义是说这个是输入数据的通道数，当这里的r=1(代表第一层)，就是第一层(第一个模块的输入时)=F，也就是说第一层输入的特征数就是所有的特征，当r=2时，可能输入的特征数会发生改变?(这里我还没看明白)，然后

是可学习的参数。(具体这个学习更新是根据标签y与y-hat的损失来更新吗？)

22.6.20

今天试着把代码跑一遍，原来github上面的是mxnet版本的，后面又找到了一个别人修改好的pytorch版本，看来这篇论文被很多人复现过。

但是今天用pycharm跑根本跑不动，光数据集就加载了50分钟，后面训练直接卡死了。可能是模型太大了。只有一点点自己看下去，不能用pycharm的debug帮我跑代码了。

今天关于图卷积理论部分看明白了从谱域和空域两个不同角度来分析的不同点，

空域的角度：公式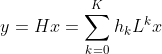： 其中L是拉普拉斯矩阵，相当于一种聚合图上邻居节点的操作，一阶的拉普拉斯算子聚合一阶邻居，二阶的拉普拉斯算子聚合二阶的邻居节点。h是各阶算子的系数，就是可以学习的参数。

频域角度: 由于 ，y可以写成 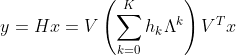,h相当于一个滤波器，控制得到我们想要的频率响应特性之后再转换回空域。

频域的缺点：需要进行特征值分解，计算开销大，复杂度为O(3),

为了降低计算复杂度，有文章对频域角度出发的公式做了简化，控制K的大小，使其为0,1，这样原来的公式可以化为较为简单的形式，并且由于K为0和1，计算出来和V，VT运算，发现不需要特征值分解了，降低了复杂度。

然后ASTGCN这篇文章并没有使K为0和1，而是用了切比雪夫多项式做近似，用切比雪夫多项式的好处是也不用做特征值分解了，并且可以保留高阶项。

今天就看了这么多，因为模型太大了电脑跑不起来，所以具体的代码只有自己慢慢看了。明天继续