2012 Multi-University Training Contest 4
1001 Image Recognition
题解:
本题题目大意在一个01方阵中找出四条边全都是1的正方形的个数,对于正方形内部则没有要求。
一个直观的想法是首先用N^2的时间预处理出每一个是1的点向上下左右四个方向能够延伸的1的最大长度,记为四个数组l, r, u, d。然后我们观察到正方形有一个特征是同一对角线上的两个顶点在原方阵的同一条对角线上。于是我们可以想到枚举原来方阵的每条对角线,然后我们对于每条对角线枚举对角线上所有是1的点i,那么我们可以发现可能和i构成正方形的点应该在该对角线的 [i, i + min(r[i], d[i]) – 1] 闭区间内, 而在这个区间内的点 j 只要满足 j – i + 1 <= min(l[j], u[j]) 也就是满足j – min(l[j], u[j]) + 1 <= i,这样的 (i, j) 就能构成一个正方形。也就是说对于每条对角线,我们可以构造一个数组 a, 使得a[i] = i – min(l[i], u[i]) + 1
然后对这个数组有若干次查询,每次查询的是区间 [i, i + min(r[i], d[i]) – 1]内有多少个数满足 a[j] <= i,所有这些问题答案的和就是该问题的结果。对于这个问题,我们可以通过离线算法,先保存所有查询的区间端点,并对所有端点排序。然后使用扫描线算法,如果扫描到的是第i次查询的左端点,就让当前结果减去当前扫描过的数中 <= i的个数,如果扫描到的是第i次查询的有短点,则让当前结果加上当前扫描过的数中 <= i的个数,最后所有结果相加即可。
维护当前数出现的个数可以使用树状数组。这样对于每条对角线求结果的复杂度为O(nlogn),算法总的复杂度为O(n^2logn)。
1002 Constructing Chimney
题解:
本题注意到数据规模显然需要通过求得递推关系矩阵,然后由矩阵快速幂求解。
求递推关系矩阵的过程可以使用状态压缩dp的方法。
我们对于最后一层的8个点,用0和1表示两种不同的状态,其中0表示在本层这里为空,需要下一层来填满,1表示本层这里已经填满。这样我们可以发现下层为0的地方上一层必须为1,上下两层均为1的地方,必须保证下层能够通过横放得到,即不能有单独的1存在,这样通过状态压缩dp即可获得相邻两层的递推关系,另外需要注意的是两层之间
1 1 1 状态之间转移时有两种方法,其它状态之间的转移都是1种方法。
1 1
1 1 1
1003 Revolving Digits
题解:
本题重点是比较x经过数位轮换之后的每个数和x的大小关系。由于x很大,我们需要将x以及轮换后的每个数视为一个长度为x长度的字符串,然后进行字符串比较。也就是说,我们可以将x后面接上一个x,变为xx,然后比较xx前n位以每一位开头长度为n的字符串与xx前n位的大小。如果我们能够很快求出xx的每一位和xx的最长公共前缀的长度的话,比较大小我们只需要O(1)的时间,而求出每一位的最长公共前缀可以使用扩展KMP算法在O(n)时间内求得,这样就可以在O(n)时间内完成所有的比较。
除了比较之外,本题还需要对于数字进行判重,经过观察我们发现,轮换出现重复数字的情况说明原来的x存在循环节,我们只需要找出x的最小循环节,然后只比较循环节之内的数即可。而求最小循环节也可以通过扩展KMP算法或者KMP算法得出,这样整体时间复杂度为O(n)。
1004 Trouble
If we have two sorted lists of integers A and B, we can easily find in linear time by keeping two pointers if there are a in A and b in B such that a+b=c (c is given).
Now, for this problem, we create a sorted list of all sums for S[0] and S[1] (call it M[0]), and a sorted list of all sums for S[2] and S[3] (call it M[1]). We can do this in O(n^2 log n).
Then, for each member c of S[4], we find if there's a in M[0] and b in M[1] such that a+b+c=0 using the method described in paragraph one. Sinc each search takes O(n^2) time (because the size of lists are O(n^2)), and we have O(n) members in S[4], total time complexity of this algorithm will be O(n^3).
1005 What is N?
本题属于简单题
(1) n如果很大,那么n! mod phi(P) 为0, 于是问题等价为

于是我们可以求得
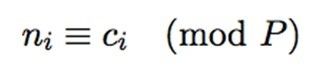
求的方法无非就是暴力FOR + 二分求幂 即可
(2) 对于比较小的n,我们可以采取暴力枚举的方法
1006 Card Collector
中等偏难的概率/组合数学。设卡片的分布p=(p1,p2,...,pn),T(p)表示拿到所有卡片时买的零食数目,有
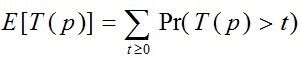
由容斥原理得,

1007 King Arthur's Knights
中等题,构造一个特殊图的Hamilton回路。首先随机得到一个环序列a1, a2, ..., an, 如果a(i)->a(i+1)在图中没有边,因为每个点至少和一半的点有边相连,于是一定可以找到另一个点j,满足a(i)-a(j)有边,a(i+1)-a(j+1)有边。然后反转环中a(i+1)到a(j)这一段序列,即可令环上存在的边数增加1或2(取决于原来的环上a(j)->a(j+1)是否有边)。继续此过程直到环上所有的边都存在。
1008
对于有n个点,m条边,q个询问的图,先求出割点与双联通分量,然后缩点建树。该树满足一个条件,即树中相邻的点一定满足一个是双联通分量,一个是割点。一个非常容易证明的结论是,同一个双连通分量中的两个点,一定存在一条简单路径。有了这个结论,可以得到如下算法:对于每个询问,首先判断两个点是否相同,如果相同,答案为n – 1。否则,如果这两个点在原图中不连通,答案为0。否则,将双联通分量在树种所对应的点看成白色,割点所对应的点看成黑色。统计路径上总共有多少个点,这还并非所有能处于询问中的两点的简单路径上的点。答案。因为从白色点出发走一步所能走到的黑色点,无论是否处于询问的两个点在树中所对应的路径上,都可以是处于两点间的简单路径上的点,所以要加上这些点。最后的答案是n减去这个值。
此题主要需要求割点,双联通分量,LCA,割点和双联通分量部分的复杂度是o(m),LCA为o(nlgn),询问的复杂度为o(qlogn)总复杂度为o(nlogn + m)。
此题的trick有如下几个地方:
1. 询问的两个点不连通
2. 询问的两个点相同
3. 孤立点既不是双联通分量,也不是割点。
4. 一个n个点的图,缩点建树后可能有2 * n – 1个点
1009
We can compare two substrings using hash (s[0]*(p^0)+s[1]*(p^1)+...+s[i]*(p^i), where ^ means power).
Let's n be 1+max(l1, l2). For i (l1<=i and i<n) put s1[i]='1', j (l2<=j and j<n) s2[j]='2'.
We can build segment tree for each string (now they have length n).
In each node we save hash of substring [l..r].
So if vertex v has 2 sons l and r than t[v]=t[l]+t[r]*p^(length of l).
For 1-st query just go down and modify t (see solution).
For 2-nd - go upper in tree until substrings in right vertex are not equal. Then add to current length, the length of the largest common prefix in right vertex (easily going down in tree, see solution).
It's O(n+Q*log(n)).
Another solution without hashes is to recalc values f[], g[], where f[i]==j is minimum j, that s1[j..i]==s2[j..i]. And g[i]==j is maximum j, that s1[i..j]==s2[i..j]. It's O(n+Q*log(n)) too.