Pytorch学习笔记(2)-常用函数与概念
文章目录
-
-
-
- 1.指定运行设备
- 2.稀疏矩阵
- 3.四则运算
- 4.矩阵运算
- 5.幂、开方、对数运算
- 6.in-place操作
- 7.广播机制
- 8.取整、取余、比较、top-k
- 9.判定异常值
- 10.三角函数
- 11.统计函数
-
-
1.指定运行设备
pytorch可以指定数据运行在cpu或者gpu上,以下为例。
import torch
#dev = torch.device("cpu")
dev = torch.device("cuda")
a = torch.tensor([2, 2],
dtype=torch.float32,
device=dev)
print(a)
>>tensor([2., 2.], device='cuda:0')
2.稀疏矩阵
稀疏矩阵可以节省表示空间,在pytorch用sparse_coo_tensor表示,其中i,表示坐标,v表示值。
i = torch.tensor([[0, 1, 2], [0, 1, 2]])
v = torch.tensor([1, 2, 3])
a = torch.sparse_coo_tensor(i, v, (4, 4),
dtype=torch.float32,
device=dev).to_dense()
print(a)
>>tensor([[1., 0., 0., 0.],
[0., 2., 0., 0.],
[0., 0., 3., 0.],
[0., 0., 0., 0.]], device='cuda:0')
3.四则运算
Pytorch支持四则运算加减乘除,其中以加法为例,有以下四种表示,其中前三种方式不改变a变量本身的值,第四种方式改变其本身的值。
c = a + b
c = torch.add(a,b)
a.add(b)
a,add_(b)
以下为代码示例:
import torch
##add
a = torch.rand(2, 3)
b = torch.rand(2, 3)
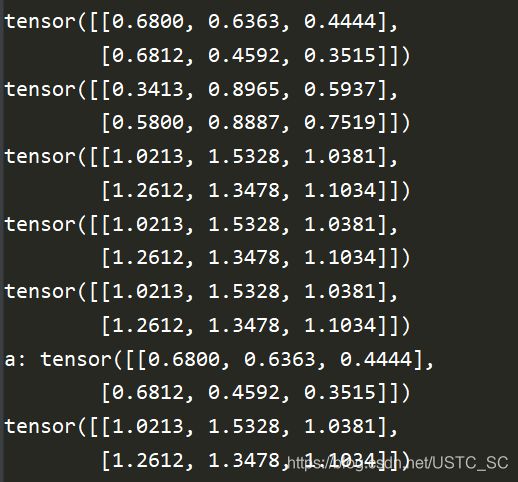
print(a)
print(b)
print(a + b)
print(a.add(b))
print(torch.add(a, b))
print("a:" ,a)
print(a.add_(b))
print("a:",a)
同理还有减法,乘法,除法运算如下
#sub
c = a - b
c = torch.sub(a,b)
a.sub(b)
a.sub_(b)
#mul(哈达玛积:对应元素相乘)
c = a * b
c = torch.mul(a,b)
a.mul(b)
a.mul_(b)
#div
c = a / b
c = torch.div(a,b)
a.div(b)
a.div_(b)
4.矩阵运算
二维矩阵乘法运算操作包括torch.mm(); torch .matmul; @ 三种方式,矩阵相乘需要满足矩阵相乘的维度要求。以下为样例
a = torch.ones(2, 1)
b = torch.ones(1, 2)
print(a @ b)
print(a.matmul(b))
print(torch.matmul(a, b))
print(torch.mm(a, b))
print(a.mm(b))
对于高维的Tensor(dim>2),定义其矩阵乘法仅在最后的两个维度上,要求前面的维度必须保持一致,就像矩阵索引一样并且运算操作只有torch.matmul(),以下为样例。
##高维tensor
a = torch.ones(1, 2, 3, 4)
b = torch.ones(1, 2, 4, 3)
print(a.matmul(b))
print(a.matmul(b).shape)
5.幂、开方、对数运算
在pytorch下幂运算有以下表示方式
#幂运算
b = torch.pow(a,2)
b = a.pow(2)
b = a ** 2
b = a.pow_(2)
#开方
b = a.sqrt()
b = a.sqrt_()
#对数运算
b = torch.log2(a)
b = torch.log10(a)
b = torch.log(a) #以e为底
b = torch.log_(a)
6.in-place操作
inplace=True的意思是进行原位操作,例如x=x+5,对x就是一个原地操作;y=x+5,x=y,完成了与x=x+5同样的功能但是不是原地操作,原位操作不允许使用临时变量。此外,我们之前学习的add_ , sub_ , mul_ 等也是原位操作。
7.广播机制
首先我们来看一下什么是广播机制,在pytorch中广播机制是指在满足特定限制的前提下,较小的数组“广播至”较大的数组,使两者形状互相兼容。而广播也需要一定的条件
-
每个张量至少有一个维度。
-
迭代维度尺寸时,从尾部的维度开始,维度尺寸
或者相等,
或者其中一个张量的维度尺寸为 1 ,
或者其中一个张量不存在这个维度。
# 以下m 和 n 可广播,且广播后的shape为5*3*4*1
m = torch.empty(5, 3, 4, 1)
n = torch.empty( 3, 1, 1)
# 倒数第一个维度:两者的尺寸均为1
# 倒数第二个维度:n尺寸为1
# 倒数第三个维度:两者尺寸相同
# 倒数第四个维度:n该维度不存在
8.取整、取余、比较、top-k
.floor() #向下取整
.ceil() #向上取整
.round() #四舍五入
.trunc() #裁剪,只取整数部分
.frac() #只取小数部分
% #取余
---------------------
torch.eq(input,other,out=None) #按成员进行等式操作,相同返回True
torch.equal(tensor1,tensor2) #如果tensor1和tensor2有想同的size 和elements,则为True
torch.ge(input,other,out=None) #input>=other
torch.gt(input,other,out=None) #input>other
torch.le(input,other,out=None) #input<=other
torch.lt(input,other,out=None) #input>other
torch.ne(input,other,out=None) #input!=other
------------------------
torch.sort(input,dim=None,decending = False,out = None) #对目标input进行排序
torch.topk(input,k,dim = None,largest,sorted = True,out = None)#沿着指定维度返回最大K个数值及其索引
torch.kthvalue(input,k,dim = None,out=None) #沿着指定维度返回第K个最小值
#案例
a = torch.tensor([[1, 4, 4, 3, 5],
[2, 3, 1, 3, 5]])
print(a.shape)
print(torch.sort(a, dim=0,
descending=False))
#topk,第二维度取top-2
a = torch.tensor([[2, 4, 3, 1, 5],
[2, 3, 5, 1, 4]])
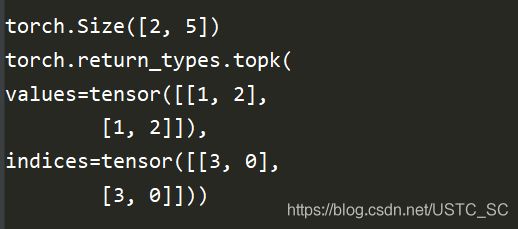
print(a.shape)
print(torch.topk(a, k=2, dim=1, largest=False))
9.判定异常值
可通过torch.isfinite(tensor) /torch.isinf(tensor) /torch.isnan(tensor)来对张量进行判断
a = torch.rand(2, 3)
print(a)
print(a/0)
print(torch.isfinite(a))
print(torch.isfinite(a/0))
print(torch.isinf(a/0))
print(torch.isnan(a))
10.三角函数
#常用的三角函数如下
torch.abs(input,out = None)
torch.sin(input,out = None)
torch.sinh(input,out = None)
torch.asin(input,out = None)
torch.cos(input,out = None)
torch.tan(input,out = None)
#其他比较常用的数学函数
torch.sign()
torch.sigmoid()
11.统计函数
- torch.mean() #返回平均值
- torch.sum() #返回总和
- torch.prod() # 计算所有元素积
- torch.max() #返回最大值
- torch.min() #返回最小值
- torch.argmax() #返回最大值排序的索引值
- torch.argmin() #返回最小值排序的索引值
- torch.std() #返回标准差
- torch.var() #返回方差
- torch.median() #返回中间值
- torch.mode() #返回众数
- torch.histc() #计算input的直方图
- torch.bincount() #返回每个值的频数
import torch
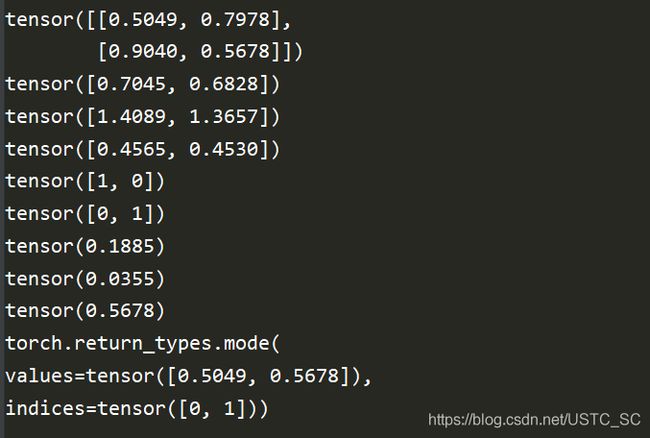
a = torch.rand(2, 2)
print(a)
print(torch.mean(a, dim=0))
print(torch.sum(a, dim=0))
print(torch.prod(a, dim=0))
print(torch.argmax(a, dim=0))
print(torch.argmin(a, dim=0))
print(torch.std(a))
print(torch.var(a))
print(torch.median(a))
print(torch.mode(a))