图像分类-神经网络结构，（leetcode704 278）
常见的图像分类的CNN网络
1.AlexNet
1.1AlexNet介绍
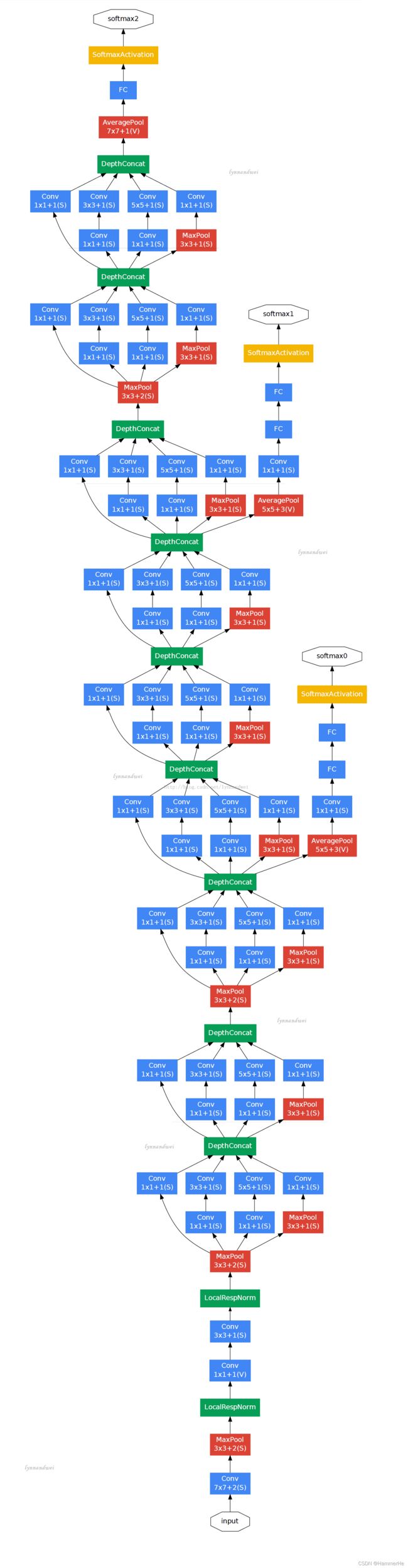
AlexNet是用于图像分类的CNN模型，具体的结构如下（可以看这个帖子了解每一层的内容）
4个优点：
1.ReLU激活函数的引入
采用修正线性单元(ReLU)的深度卷积神经网络训练时间比等价的tanh单元要快几倍。而时间开销是进行模型训练过程中很重要的考量因素之一。同时，ReLU有效防止了过拟合现象的出现。由于ReLU激活函数的高效性与实用性，使得它在深度学习框架中占有重要地位。
2.层叠池化操作
以往池化的大小PoolingSize与步长stride一般是相等的，例如：图像大小为256*256，PoolingSize=2×2，stride=2，这样可以使图像或是FeatureMap大小缩小一倍变为128，此时池化过程没有发生层叠。但是AlexNet采用了层叠池化操作，即PoolingSize > stride。这种操作非常像卷积操作，可以使相邻像素间产生信息交互和保留必要的联系。论文中也证明，此操作可以有效防止过拟合的发生。
3.Dropout操作
Dropout操作会将概率小于0.5的每个隐层神经元的输出设为0，即去掉了一些神经节点，达到防止过拟合。那些“失活的”神经元不再进行前向传播并且不参与反向传播。这个技术减少了复杂的神经元之间的相互影响。在论文中，也验证了此方法的有效性。
4.网络层数的增加
与原始的LeNet相比，AlexNet网络结构更深，LeNet为5层，AlexNet为8层。在随后的神经网络发展过程中，AlexNet逐渐让研究人员认识到网络深度对性能的巨大影响。当然，这种思考的重要节点出现在VGG网络（下文中将会讲到），但是很显然从AlexNet为起点就已经开始了这项工作。
1.2 Alexnet TF复现
选了很多组batch size进行测试，最高识别率还不到60，感觉效果一般，也可能是我代码有问题。
"""
输入参数：
x=数据集
keep_prob=用于DropOut，表示input中的元素被保留下来的概率.
num_classes=类别数目，如该项目中只有猫和狗，所以类别是2
"""
import tensorflow as tf
def Alexnet(x, keep_prob, num_classes):
# conv1
with tf.name_scope('conv1') as scope:
kernel = tf.Variable(tf.truncated_normal([11, 11, 3, 96], dtype=tf.float32, stddev=1e-1), name='weights')
conv = tf.nn.conv2d(x, kernel, [1, 4, 4, 1], padding='SAME')
biases = tf.Variable(tf.constant(0.0, shape=[96], dtype=tf.float32), trainable=True, name='biases')
bias = tf.nn.bias_add(conv, biases)
conv1 = tf.nn.relu(bias, name=scope)
# lr1
with tf.name_scope('lrn1') as scope:
lrn1 = tf.nn.local_response_normalization(conv1, alpha=1e-4, beta=0.75, depth_radius=2, bias=2.0)
# pool1
with tf.name_scope('pool1') as scope:
pool1 = tf.nn.max_pool(lrn1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='VALID')
# conv2
with tf.name_scope('conv2') as scope:
pool1_groups = tf.split(axis=3, value=pool1, num_or_size_splits=2)
kernel = tf.Variable(tf.truncated_normal([5, 5, 48, 256], dtype=tf.float32, stddev=1e-1), name='weights')
kernel_groups = tf.split(axis=3, value=kernel, num_or_size_splits=2)
conv_up = tf.nn.conv2d(pool1_groups[0], kernel_groups[0], [1, 1, 1, 1], padding='SAME')
conv_down = tf.nn.conv2d(pool1_groups[1], kernel_groups[1], [1, 1, 1, 1], padding='SAME')
biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32), trainable=True, name='biases')
biases_groups = tf.split(axis=0, value=biases, num_or_size_splits=2)
bias_up = tf.nn.bias_add(conv_up, biases_groups[0])
bias_down = tf.nn.bias_add(conv_down, biases_groups[1])
bias = tf.concat(axis=3, values=[bias_up, bias_down])
conv2 = tf.nn.relu(bias, name=scope)
# lrn2
with tf.name_scope('lrn2') as scope:
lrn2 = tf.nn.local_response_normalization(conv2, alpha=1e-4, beta=0.75, depth_radius=2, bias=2.0)
# pool2
with tf.name_scope('pool2') as scope:
pool2 = tf.nn.max_pool(lrn2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='VALID')
# conv3
with tf.name_scope('conv3') as scope:
kernel = tf.Variable(tf.truncated_normal([3, 3, 256, 384], dtype=tf.float32, stddev=1e-1), name='weights')
conv = tf.nn.conv2d(pool2, kernel, [1, 1, 1, 1], padding='SAME')
biases = tf.Variable(tf.constant(0.0, shape=[384], dtype=tf.float32), trainable=True, name='biases')
bias = tf.nn.bias_add(conv, biases)
conv3 = tf.nn.relu(bias, name=scope)
with tf.name_scope("conv4") as scope:
conv3_groups = tf.split(axis=3, value=conv3, num_or_size_splits=2)
kernel = tf.Variable(tf.truncated_normal([3, 3, 192, 384], dtype=tf.float32, stddev=1e-1), name='weights')
kernel_groups = tf.split(axis=3, value=kernel, num_or_size_splits=2)
conv_up = tf.nn.conv2d(conv3_groups[0], kernel_groups[0], [1, 1, 1, 1], padding="SAME")
conv_down = tf.nn.conv2d(conv3_groups[1], kernel_groups[1], [1, 1, 1, 1], padding="SAME")
biases = tf.Variable(tf.constant(0.0, shape=[384], dtype=tf.float32), trainable=True, name='biases')
biases_groups = tf.split(axis=0, value=biases, num_or_size_splits=2)
bias_up = tf.nn.bias_add(conv_up, biases_groups[0])
bias_down = tf.nn.bias_add(conv_down, biases_groups[1])
bias = tf.concat(axis=3, values=[bias_up, bias_down])
conv4 = tf.nn.relu(bias, name=scope)
with tf.name_scope("conv5") as scope:
conv4_groups = tf.split(axis=3, value=conv4, num_or_size_splits=2)
kernel = tf.Variable(tf.truncated_normal([3, 3, 192, 256], dtype=tf.float32, stddev=1e-1), name='weights')
kernel_groups = tf.split(axis=3, value=kernel, num_or_size_splits=2)
conv_up = tf.nn.conv2d(conv4_groups[0], kernel_groups[0], [1, 1, 1, 1], padding='SAME')
conv_down = tf.nn.conv2d(conv4_groups[1], kernel_groups[1], [1, 1, 1, 1], padding='SAME')
biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32), trainable=True, name='biases')
biases_groups = tf.split(axis=0, value=biases, num_or_size_splits=2)
bias_up = tf.nn.bias_add(conv_up, biases_groups[0])
bias_down = tf.nn.bias_add(conv_down, biases_groups[1])
bias = tf.concat(axis=3, values=[bias_up, bias_down])
conv5 = tf.nn.relu(bias, name=scope)
with tf.name_scope("pool5") as scope:
pool5 = tf.nn.max_pool(conv5, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='VALID')
with tf.name_scope("flattened6") as scope:
flattened = tf.reshape(pool5, shape=[-1, 6 * 6 * 256])
with tf.name_scope("fc6") as scope:
weights = tf.Variable(tf.truncated_normal([6 * 6 * 256, 4096], dtype=tf.float32, stddev=1e-1), name='weights')
biases = tf.Variable(tf.constant(0.0, shape=[4096], dtype=tf.float32), trainable=True, name='biases')
bias = tf.nn.xw_plus_b(flattened, weights, biases)
fc6 = tf.nn.relu(bias)
with tf.name_scope("dropout6") as scope:
dropout6 = tf.nn.dropout(fc6, keep_prob)
with tf.name_scope("fc7") as scope:
weights = tf.Variable(tf.truncated_normal([4096, 4096], dtype=tf.float32, stddev=1e-1), name='weights')
biases = tf.Variable(tf.constant(0.0, shape=[4096], dtype=tf.float32), trainable=True, name='biases')
bias = tf.nn.xw_plus_b(dropout6, weights, biases)
fc7 = tf.nn.relu(bias)
with tf.name_scope("dropout7") as scope:
dropout7 = tf.nn.dropout(fc7, keep_prob)
with tf.name_scope("fc8") as scope:
weights = tf.Variable(tf.truncated_normal([4096, num_classes], dtype=tf.float32, stddev=1e-1), name='weights')
biases = tf.Variable(tf.constant(0.0, shape=[num_classes], dtype=tf.float32), trainable=True, name='biases')
fc8 = tf.nn.xw_plus_b(dropout7, weights, biases)
return fc8
2.VGG
2.1VGG结构的特点介绍
VGG16相比AlexNet的一个改进是采用连续的几个3x3的卷积核代替AlexNet中的较大卷积核（11x11，7x7，5x5）。
简单来说，在VGG中，使用了3个3x3卷积核来代替7x7卷积核，使用了2个3x3卷积核来代替5*5卷积核，这样做的主要目的是在保证具有相同感知野的条件下，提升了网络的深度，在一定程度上提升了神经网络的效果。如下图所示就是2个3x3卷积核来代替55卷积核：
2个3x3卷积核来代替55卷积核
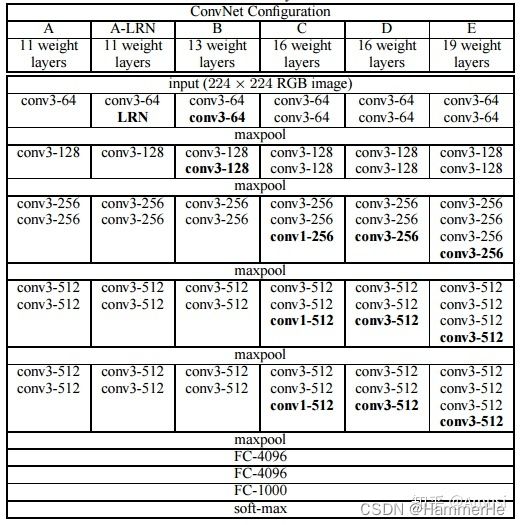
常见的VGG结构有如下几种，其中E（即VGG19）是较为常见的VGG架构：
2.2VGG16复现（tf）
想要19层的话就是在3，4，5卷积层再加3个卷积核
测试效果比Alexnet好一些，能跑出来70左右，我也不知道该调些啥 后续再优化吧，先了解一下结构。
import tensorflow as tf
'''
定义卷积层函数
'''
def conv_op(input_op, name, kh, kw, n_out, dh, dw, p):
n_in = input_op.get_shape()[-1].value
with tf.name_scope(name) as scope:
# 初始化权重
# kernel = tf.get_variable(scope + "w", shape=[kh, kw, n_in, n_out], dtype=tf.float32, initializer=tf.contrib.layers.xavier_initializer_conv2d())
kernel = tf.Variable(tf.truncated_normal([kh, kw, n_in, n_out], dtype=tf.float32, stddev=1e-1), name='weights')
# 卷积
conv = tf.nn.conv2d(input_op, kernel, (1, dh, dw, 1), padding="SAME")
# 初始化偏置
bias_init_val = tf.constant(0.0, shape=[n_out], dtype=tf.float32)
biases = tf.Variable(bias_init_val, trainable=True, name="b")
bias = tf.nn.bias_add(conv, biases)
activation = tf.nn.relu(bias, name=scope)
# 保存参数
p += [kernel, biases]
return activation
'''
定义全连接层函数
'''
def fc_op(input_op, name, n_out, p):
n_in = input_op.get_shape()[-1].value
with tf.name_scope(name) as scope:
# 初始化全连接的权重
kernel = tf.get_variable(scope + "w", shape=[n_in, n_out], dtype=tf.float32,
initializer=tf.contrib.layers.xavier_initializer())
# kernel = tf.Variable(tf.truncated_normal([6 * 6 * 256, 4096], dtype=tf.float32, stddev=1e-1), name='weights')
# 初始化全连接层的偏置
biases = tf.Variable(tf.constant(0.1, shape=[n_out], dtype=tf.float32), name="b")
# 将输入与权重的乘法和偏置的加法合并
# activation = tf.nn.relu_layer(input_op, kernel, biases, name=scope)
activation = tf.nn.xw_plus_b(input_op, kernel, biases)
return activation
'''
定义最大池化层
'''
def max_pool(input_op, name, kh, kw, dh, dw):
return tf.nn.max_pool(input_op, ksize=[1, kh, kw, 1], strides=[1, dh, dw, 1]
, padding="VALID", name=name)
'''
VGG16
'''
def VGG_16(input_op, keep_prob, num_classes):
p = []
# 第一层的第一层卷积
conv1_1 = conv_op(input_op, name="conv1_1", kh=3, kw=3, n_out=64, dh=1, dw=1, p=p)
# 第一层的第二层卷积
conv1_2 = conv_op(conv1_1, name="conv1_2", kh=3, kw=3, n_out=64, dh=1, dw=1, p=p)
# 最大池化层
pool1 = max_pool(conv1_2, name="pool1", kh=2, kw=2, dw=2, dh=2)
# 第二层的第一层卷积
conv2_1 = conv_op(pool1, name="conv2_1", kh=3, kw=3, n_out=128, dh=1, dw=1, p=p)
# 第二层的第二层卷积
conv2_2 = conv_op(conv2_1, name="conv2_2", kh=3, kw=3, n_out=128, dh=1, dw=1, p=p)
# 第二层的最大池化
pool2 = max_pool(conv2_2, name="pool2", kh=2, kw=2, dh=2, dw=2)
# 第三层
conv3_1 = conv_op(pool2, name="conv3_1", kh=3, kw=3, n_out=256, dh=1, dw=1, p=p)
conv3_2 = conv_op(conv3_1, name="conv3_2", kh=3, kw=3, n_out=256, dh=1, dw=1, p=p)
conv3_3 = conv_op(conv3_2, name="conv3_3", kh=3, kw=3, n_out=256, dh=1, dw=1, p=p)
pool3 = max_pool(conv3_3, name="pool3", kh=2, kw=2, dh=2, dw=2)
# 第四层
conv4_1 = conv_op(pool3, name="conv4_1", kh=3, kw=3, n_out=512, dh=1, dw=1, p=p)
conv4_2 = conv_op(conv4_1, name="conv4_2", kh=3, kw=3, n_out=512, dh=1, dw=1, p=p)
conv4_3 = conv_op(conv4_2, name="conv4_3", kh=3, kw=3, n_out=512, dh=1, dw=1, p=p)
pool4 = max_pool(conv4_3, name="pool4", kh=2, kw=2, dh=2, dw=2)
# 第五层
conv5_1 = conv_op(pool4, name="conv5_1", kh=3, kw=3, n_out=512, dh=1, dw=1, p=p)
conv5_2 = conv_op(conv5_1, name="conv5_2", kh=3, kw=3, n_out=512, dh=1, dw=1, p=p)
conv5_3 = conv_op(conv5_2, name="conv5_3", kh=3, kw=3, n_out=512, dh=1, dw=1, p=p)
pool5 = max_pool(conv5_3, name="pool5", kh=2, kw=2, dh=2, dw=2)
# 将pool5展平
pool5_shape = pool5.get_shape()
flattened_shape = pool5_shape[1].value * pool5_shape[2].value * pool5_shape[3].value
resh1 = tf.reshape(pool5, [-1, flattened_shape], name="resh1")
# 全连接层
fc6 = fc_op(resh1, name="fc6", n_out=4096, p=p)
fc6_drop = tf.nn.dropout(fc6, keep_prob, name="fc6_drop")
# 全连接层
fc7 = fc_op(fc6_drop, name="fc7", n_out=4096, p=p)
fc7_drop = tf.nn.dropout(fc7, keep_prob, name="fc7_drop")
fc8 = fc_op(fc7_drop, name="fc8", n_out=num_classes, p=p)
# softmax = tf.nn.softmax(fc8)
# predictions = tf.argmax(softmax, 1)
# return predictions, softmax, fc8, p
return fc8
3.GoogLeNet
3.1 Googlenet各版本结构介绍
一个完整介绍帖子
关于Inception的一点介绍：
（1）是为了代替人工确定卷积层中的过滤器类型或者确定是否需要创建卷积层和池化层；不需要人为的决定使用哪个过滤器，是否需要池化层等，由网络自行决定这些参数；即：预先给网络添加所有可能值，将输出连接起来，让网络自己学习它需要什么样的参数。
而且Inception 网络有个问题：网络的超参数设定的针对性比较强，当应用在别的数据集上时需要修改许多参数，因此可扩展性一般。所以正常使用的时候VGG效果可能会适用性更强。
3.1.1 Inception V1网络
特点介绍：
（1）提出Inception Architecture这个组件（2）建立Bottleneck Layer使用NiN的1x1卷积进行特征降维（3）取消全连接由全局平均池化替代（4）设置辅助分类器解决前几层的梯度消失问题
Inception V1网络主要在于提出了Inception Architecture这个组件，然后通过一次性尝试多种卷积核的方式增加了网络对多尺度的适应性以及增加网络宽度。
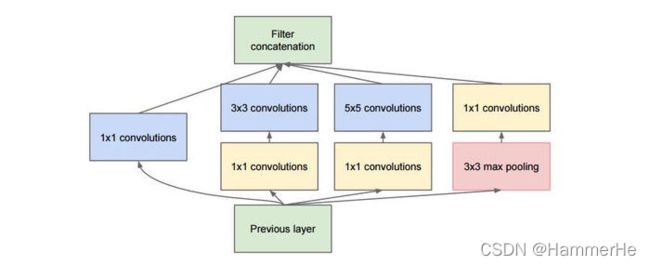inception结构的主要贡献有两个：一是使用1x1的卷积来进行升降维；二是在多个尺寸上同时进行卷积再聚合。
3.1.1.1 1X1的卷积核起到什么作用的呢？
（1）在相同尺寸的感受野中叠加更多的卷积，能提取到更丰富的特征。形象的说，如同一根吸管插入到多个通道里，然后混合多通道的特征信息，然后再以另一种通道数输出。
（2）使用1x1卷积进行降维，降低了计算复杂度。图2中间3x3卷积和5x5卷积前的1x1卷积都起到了这个作用。当某个卷积层输入的特征数较多，对这个输入进行卷积运算将产生巨大的计算量；如果对输入先进行降维，减少特征数后再做卷积计算量就会显著减少。下图是优化前后两种方案的乘法次数比较：
同样是输入一组有192个特征、32x32大小，输出256组特征的数据，第一张图直接用3x3卷积实现，需要192x256x3x3x32x32=452984832次乘法；
第二张图先用1x1的卷积降到96个特征，再用3x3卷积恢复出256组特征，需要192x96x1x1x32x32+96x256x3x3x32x32=245366784次乘法，使用1x1卷积降维的方法节省了一半的计算量。
有人会问，用1x1卷积降到96个特征后特征数不就减少了么，会影响最后训练的效果么？答案是否定的，只要最后输出的特征数不变（256组），中间的降维类似于压缩的效果，并不影响最终训练的结果。
3.1.1.2 什么是多个尺寸上同时进行卷积再聚合
图中可以看到对输入做了4个分支，分别用不同尺寸的filter进行卷积或池化，最后再在特征维度上拼接到一起。这种全新的结构有什么好处呢？
好处1：
在直观感觉上在多个尺度上同时进行卷积，能提取到不同尺度的特征。特征更为丰富也意味着最后分类判断时更加准确。
好处2：
利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度。举个例子下图左侧是个稀疏矩阵（很多元素都为0，不均匀分布在矩阵中），和一个2x2的矩阵进行卷积，需要对稀疏矩阵中的每一个元素进行计算；如果像右图那样把稀疏矩阵分解成2个子密集矩阵，再和2x2矩阵进行卷积，稀疏矩阵中0较多的区域就可以不用计算，计算量就大大降低。
这个原理应用到inception上就是要在特征维度上进行分解！传统的卷积层的输入数据只和一种尺度（比如3x3）的卷积核进行卷积，输出固定维度（比如256个特征）的数据，所有256个输出特征基本上是均匀分布在3x3尺度范围上，这可以理解成输出了一个稀疏分布的特征集；而inception模块在多个尺度上提取特征（比如1x1，3x3，5x5），输出的256个特征就不再是均匀分布，而是相关性强的特征聚集在一起（比如1x1的的96个特征聚集在一起，3x3的96个特征聚集在一起，5x5的64个特征聚集在一起），这可以理解成多个密集分布的子特征集。这样的特征集中因为相关性较强的特征聚集在了一起，不相关的非关键特征就被弱化，同样是输出256个特征，inception方法输出的特征“冗余”的信息较少。用这样的“纯”的特征集层层传递最后作为反向计算的输入，自然收敛的速度更快。
好处3：
用在inception结构中就是要把相关性强的特征汇聚到一起
3.1.1.3 全局平均池化取代全连接层
3.1.1.4 辅助分类器
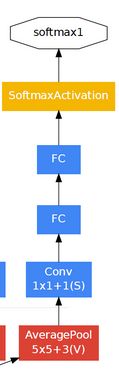
利用了2个辅助分类器反向传播，避免梯度消失的问题，特点如下：
（1）深网络中，梯度回传到最初几层，存在严重消失问题
（2）有效加速收敛
（3）测试阶段不使用
辅助分类器能加快深层网络的收敛，即通过将有用的梯度传到底层，并通过防止梯度消失来提升收敛性。但是只有在训练快结束时，利用辅助分类器才有好的效果，并且推测辅助分类器相当于一个正则化因子。
3.1.1.5 Google全局结构图
3.1.2 Inception V2网络
相比于V1版本做了如下改动：
（1）在卷积和激活函数之间-增加了Batch Normalization（批归一化），变成了卷积->BN->ReLU结构 如下所示：
其中添加了一组逆算子：scale乘子, bias偏置
这是一组需要学习的参数
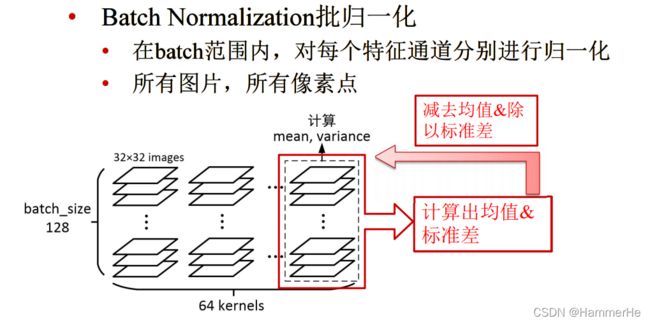（2）把Inception里面5X5的卷积核变成了2个3X3
3.1.3 Inception V3网络
减少了Inception的结构，V3具体结构如图：
figure567
引入了非对称卷积的方法，把N x N 分解成 1 x N -> N x 1从而降低参数数量和计算量，相当于把Inception层变成了如下三种形式
3.2GoogleNet V1复现
from tensorflow.keras import layers, models, Model, Sequential
def GoogLeNet(im_height=224, im_width=224, class_num=1000, aux_logits=False):
# 输入224*224的3通道彩色图片
input_image = layers.Input(shape=(im_height, im_width, 3), dtype="float32")
x = layers.Conv2D(64, kernel_size=7, strides=2, padding="SAME", activation="relu", name="conv2d_1")(input_image)
x = layers.MaxPool2D(pool_size=3, strides=2, padding="SAME", name="maxpool_1")(x)
x = layers.Conv2D(64, kernel_size=1, activation="relu", name="conv2d_2")(x)
x = layers.Conv2D(192, kernel_size=3, padding="SAME", activation="relu", name="conv2d_3")(x)
x = layers.MaxPool2D(pool_size=3, strides=2, padding="SAME", name="maxpool_2")(x)
# Inception模块
x = Inception(64, 96, 128, 16, 32, 32, name="inception_3a")(x)
x = Inception(128, 128, 192, 32, 96, 64, name="inception_3b")(x)
x = layers.MaxPool2D(pool_size=3, strides=2, padding="SAME", name="maxpool_3")(x)
# Inception模块
x = Inception(192, 96, 208, 16, 48, 64, name="inception_4a")(x)
# 判断是否使用辅助分类器1。训练时使用，测试时去掉。
if aux_logits:
aux1 = InceptionAux(class_num, name="aux_1")(x)
# Inception模块
x = Inception(160, 112, 224, 24, 64, 64, name="inception_4b")(x)
x = Inception(128, 128, 256, 24, 64, 64, name="inception_4c")(x)
x = Inception(112, 144, 288, 32, 64, 64, name="inception_4d")(x)
# 判断是否使用辅助分类器2。训练时使用，测试时去掉。
if aux_logits:
aux2 = InceptionAux(class_num, name="aux_2")(x)
# Inception模块
x = Inception(256, 160, 320, 32, 128, 128, name="inception_4e")(x)
x = layers.MaxPool2D(pool_size=3, strides=2, padding="SAME", name="maxpool_4")(x)
# Inception模块
x = Inception(256, 160, 320, 32, 128, 128, name="inception_5a")(x)
x = Inception(384, 192, 384, 48, 128, 128, name="inception_5b")(x)
# 平均池化层
x = layers.AvgPool2D(pool_size=7, strides=1, name="avgpool_1")(x)
# 拉直
x = layers.Flatten(name="output_flatten")(x)
x = layers.Dropout(rate=0.4, name="output_dropout")(x)
x = layers.Dense(class_num, name="output_dense")(x)
aux3 = layers.Softmax(name="aux_3")(x)
# 判断是否使用辅助分类器
if aux_logits:
model = models.Model(inputs=input_image, outputs=[aux1, aux2, aux3])
else:
model = models.Model(inputs=input_image, outputs=aux3)
return model
class Inception(layers.Layer):
# ch1x1, ch3x3red, ch3x3, ch5x5red, ch5x5, pool_proj分别对应Inception中各个卷积核的个数,**kwargs可变长度字典变量，存放层名称
def __init__(self, ch1x1, ch3x3red, ch3x3, ch5x5red, ch5x5, pool_proj, **kwargs):
super(Inception, self).__init__(**kwargs)
# 分支1
self.branch1 = layers.Conv2D(ch1x1, kernel_size=1, activation="relu")
# 分支2
self.branch2 = Sequential([
layers.Conv2D(ch3x3red, kernel_size=1, activation="relu"),
layers.Conv2D(ch3x3, kernel_size=3, padding="SAME", activation="relu")])
# 分支3
self.branch3 = Sequential([
layers.Conv2D(ch5x5red, kernel_size=1, activation="relu"),
layers.Conv2D(ch5x5, kernel_size=5, padding="SAME", activation="relu")])
# 分支4
self.branch4 = Sequential([
layers.MaxPool2D(pool_size=3, strides=1, padding="SAME"),
layers.Conv2D(pool_proj, kernel_size=1, activation="relu")])
def call(self, inputs, **kwargs):
branch1 = self.branch1(inputs)
branch2 = self.branch2(inputs)
branch3 = self.branch3(inputs)
branch4 = self.branch4(inputs)
outputs = layers.concatenate([branch1, branch2, branch3, branch4]) # 将4个分支输出按通道连接
return outputs
class InceptionAux(layers.Layer):
# num_classes表示输出分类节点数，**kwargs存放每层名称
def __init__(self, num_classes, **kwargs):
super(InceptionAux, self).__init__(**kwargs)
self.averagePool = layers.AvgPool2D(pool_size=5, strides=3) # 平均池化
self.conv = layers.Conv2D(128, kernel_size=1, activation="relu")
self.fc1 = layers.Dense(1024, activation="relu") # 全连接层1
self.fc2 = layers.Dense(num_classes) # 全连接层2
self.softmax = layers.Softmax() # softmax激活函数
def call(self, inputs, **kwargs):
x = self.averagePool(inputs)
x = self.conv(x)
x = layers.Flatten()(x) # 拉直
x = layers.Dropout(rate=0.5)(x)
x = self.fc1(x)
x = layers.Dropout(rate=0.5)(x)
x = self.fc2(x)
x = self.softmax(x)
return x
4 ResNet （残差神经网络）
一个详细介绍ResNet的帖子
记一个知识点：
（1）神经网络的层数不是越深越好的，不断层数往上加，可能会导致梯度消失，梯度爆炸的问题，而且会造成网络退化，从而使得过拟合。
4.1Resnet结构介绍
ResNet是一种残差网络，可以把它分解成为一个个如下图的子网络，这个子网络经过堆叠可以构成一个很深的网络。
那么为什么要构建这么一个网络来堆叠出一个深层网络呢？干嘛不直接用卷积层对网络进行一个堆叠呢？
虽然网络越深，我们能获取的信息越多，而且特征也越丰富。就如刚刚提到的，根据实验表明，随着网络的加深，优化效果反而越差，测试数据和训练数据的准确率反而降低了。这是由于网络的加深会造成梯度爆炸和梯度消失的问题。如下图所示，56层反而不如20层：
目前针对这种现象已经有了解决的方法：对输入数据和中间层的数据进行BN操作，这种方法可以保证网络在反向传播中采用随机梯度下降（SGD），从而让网络达到收敛。但是，这个方法仅对几十层的网络有用，当网络再往深处走的时候，这种方法就无用武之地了。所以Resnet结构就是为了解决很深的网络梯度消失或者爆炸的问题
实际上ResNet结构图有如下两种：左边为原始结构，右边为Bootleneck优化结构
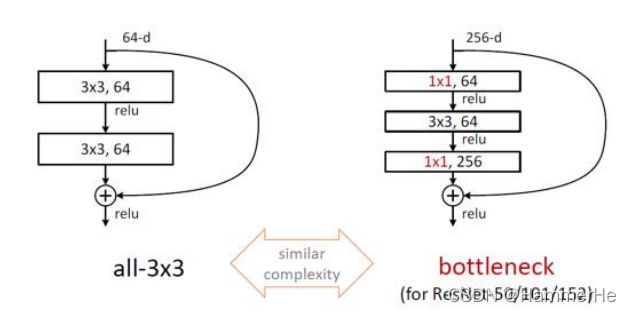
对于神经网络而言，我们最终求解的预测值映射F(X)希望和实际值即观测值映射H(X)相等，但是在残差神经网络中却不是这样的，而是问题转换为求解网络的残差映射函数，也就是F(x)，其中F(x) = H(x)-x。
残差：观测值与估计值之间的差。
这里H(x)就是观测值，x就是估计值（也就是上一层ResNet输出的特征映射）。
我们一般称x为identity Function，它是一个跳跃连接；称F(x)为ResNet Function。
那么咱们要求解的问题变成了H(x) = F(x)+x。
为什么要这样？
但是！！！！
当层数达到103的数量级时,哪怕用了残差结构，仍然会出现退化问题，这是因为当层数达到103的数量级时，退化的原因不再是因为结构优化的问题了，而是因为网络层级太深太强，而数据集太小太弱，不足以应对如此强大的残差结构，导致了过拟合。
leetcode 二分查找(704,278)
704. 二分查找
class Solution:
def search(self, nums: List[int], target: int) -> int:
low,high=0,len(nums)-1
while low <= high:
mid=(low+high)//2
if nums[mid]>target:
high=mid-1
elif nums[mid]<target:
low=mid+1
else:
return mid
return -1
278. 第一个错误的版本
第一个错误版本的定义是，前一个版本是对的 然后当前版本错了！！！
class Solution:
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
low,high=0,n
while low<=high:
mid=(low+high)//2
if isBadVersion(mid):
if not isBadVersion(mid-1):
return mid
else:
high=mid-1
else:
low=mid+1