(系列笔记)26.主成分分析——PCA(上)
文章目录
- PCA——利用数学工具提取主要特征
-
- 泛滥成灾的特征维度
-
- 维度灾难
- 数据稀疏
- 数据稀疏对机器学习的影响
- 降低数据维度
-
- 降低维度的可能
- 降维度方法
- 主成分分析(PCA)的原则
- PCA 的优化目标
-
- 基于最近重构性的优化目标
- 基于最大可分性的优化目标
PCA——利用数学工具提取主要特征
泛滥成灾的特征维度
维度灾难
维数灾难(Curse of Dimensionality,也可以直接翻译为“维度诅咒”)是一种在分析或组织高维(通常是几百维或者更高维度)数据时会遇到的现象。既然叫灾难或者诅咒,可见不是好现象。
这个说法,最早是由理查德 · 贝尔曼(Richard E. Bellman)——美国应用数学家,同时也是动态规划算法的创始人——提出来的。
他是在思考动态优化的过程中发现了这件事:当数据维度增加时,由于向量空间体积呈指数级增加,会遇到许多在低维数据中很难出现的问题。比如:
100个平均分布的点能把一个一维的单位区间均分为100份,也就是说100个均匀分布的采样点就可以在一维的单位空间里形成精度为0.01的采样。而要在二维的单位空间里形成同样密度的采样,就需要10000个点;三维需要1000000个点;十维空间则需要 1 0 20 10^{20} 1020个采样点……
那要是1000维呢?所需采样数根本就是天文数字,现实当中,我们怎么可能去找那么多样本数据?
以上是当年理查德 · 贝尔曼举的例子。
数据稀疏
其实这个问题反过来想更直接。
在现实生活中,无论我们是做统计分析还是机器学习,能获得的样本的数量(至少是量级)是相对固定的,毕竟现实数据都有其获取成本。
同样数量的样本,如果我们只选取一维特征,那么这些样本在特征空间中的密度肯定会比在二维、三维或者更高维度空间中大得多。
下图这个例子显示了20个样本,分别在一维、二维和三维空间中的分布:

而到了真正的高维,将稀疏到什么程度,可以想象。
数据稀疏对于任何要求有统计学意义的方法而言(无论是概率统计、数据挖掘,还是机器学习)都是一个问题。
一般而言,为了获得在统计学上可靠的结果,用来支撑这一结果的数据量随着特征维数的提高而呈指数级增长。
数据稀疏对机器学习的影响
数据稀疏对于机器学习的影响尤其大。
-
首先,机器学习本身就是建立在统计学习之上的。
-
-其次,在机器学习中有大量模型依据样本之间的相似度来对其进行判断,而往往样本的相似度由其在特征空间的相互距离决定,这就使得样本密度直接影响了样本属性。
-
此外,维度的增多还直接导致了对于计算能力需求的增大,从而在实践中对机器学习算法造成影响。
机器学习中,有时会出现这样的情况:在训练样本固定的情况下,特征维数增加到某一个临界点后,继续增加反而会导致模型的预测能力减小——这叫做休斯现象(Hughes Phenomenon,以其发现者 G. Hughes 命名)。
降低数据维度
降低维度的可能
虽然很多时候,“维数灾难”会被研究人员当作不处理高维数据的借口,但学术界对这一现象一直在进行研究。
由于本征维度的存在,众多降维方法的有效性得到了证明——也就是说,应用这些降维方法处理过的数据,虽然特征维度下降了,却没有丢失掉主要的属性信息。
注意:本征维度(Intrinsic Dimension)原本是信号处理中的概念。
信号的本征维度描述了需要用来表示信号的变量数量。对于含有 N个变量的信号而言,它的本征维度为M,M满足 0 ≤ M ≤ N 0\le M\le N 0≤M≤N;本征维度指出,许多高维数据集可以通过削减维度降至低维空间,而不必丢失重要信息。
降维度方法
机器学习领域里讲的降维是指:采用某种映射方法,将原本高维空间中的数据样本映射到低维空间中。
降维的本质是学习一个映射函数 y = f ( x ) y=f(x) y=f(x),其中 x 表示原始的高维数据,y 表示映射后的低维数据。
之所以降维后的数据能够不丧失主要信息,是因为原本的高维数据中包含了冗余信息和噪音,通过降维,我们减少了冗余,过滤了噪声,从而保留了有效的特征属性,甚至是提高了数据的精度——这当然是我们希望的情况。
降维算法多种多样,比较常用的有:PCA(Principal Component Analysis,主成分分析)、LDA(Linear Discriminant Analysis,线性判别分析)、LLE(Locally linear embedding,局部线性嵌入)、Laplacian Eigenmaps (拉普拉斯特征映射)等。
还有一些机器学习模型和方法,比如随机森林/决策树,聚类等,也可以用作降维的手段。
今天我们只讲其中最常用的一种——PCA,主成分分析。
主成分分析(PCA)的原则
PCA 是一种统计学中用于分析、简化数据集的技术,经常用来减少数据的维度数。
PCA 由英国数学家卡尔 · 皮尔逊(Karl Pearson)——他也是皮尔森卡方检验的发明者——在1901年发明的。在统计学领域,PCA 是最简单的用特征分析进行多元统计分布的方法。
我们对于所有降维方法的预期都是:将原始高维空间的样本数据转变为低维“子空间”(Subspace)中的数据,使得子空间中样本密度得以提高,样本间距离计算变得容易,同时又不丧失主要特征信息,至少是不丧失与学习任务有密切关系的那些特征信息。
向量空间都有对应的超平面,而超平面的维度低于其所在空间。
那么,如果我们能把一个空间中的样本点映射到它的超平面上去,这样一来,映射后的结果不就只存在于超平面空间(也就是原空间的子空间)了吗?这样,我们就获得了降维的结果。
怎么能够保证超平面中的点不丧失对应原始点的“主成分”呢?
首先,至少要尽量使得原空间中的样本点投影到超平面之后不重叠。否则,有一些样本就“消失”了——这显然不符合我们的预期。
其次,既然做了投影,就一定会丢失一部分信息。直接丢失掉的,就是原空间中样本到达超平面的距离。因此,我们还要尽量使得这个超平面靠近原空间样本点——如果样本点到超平面的距离只有很小的一段,那么映射后它丢失的信息量也相应地会很小。
基于这种想法,我们理想的超平面需要具备这样两个性质:
- 最大可分性:样本点到这个超平面上的投影尽量能够分开;
- 最近重构性:样本点到这个超平面的距离尽量近。
PCA 的优化目标
既然已经知道我们要做的是将一个向量空间中的样本投影到具备上述两个性质的超平面里面去。那么根据之前的经验,下一步就是把我们要做的事情转化为形式化优化目标。
我们的优化目标很清晰,就是最大可分性和最近重构性。形式化表达就是用数学式子来表达它(们)。
假设我们有 n 个样本数据,这些样本原本属于一个 d 维空间。
我们先对样本数据做一下中心化,使得 ∑ i x ( i ) = 0 \sum_ix^{(i)}=0 ∑ix(i)=0
原空间里的第i个样本可以表示为:

我们要将它们投影到一个d’维的空间,有 d ′ < d d'<d d′<d,第i样本投射到低维空间后标识位:
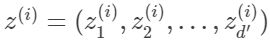
从 x ( i ) x^{(i)} x(i)到 z ( i ) z^{(i)} z(i)的转换表示为:

上式中, z j ( i ) z^{(i)}_j zj(i)表示 x ( i ) x^{(i)} x(i)在低维坐标系下的第 j j j维的坐标。
w j w_j wj是一个d维的权重向量, w j = ( w j 1 , w j 2 , . . . , w j d ) w_j=(w_{j1},w_{j2},...,w_{jd}) wj=(wj1,wj2,...,wjd)
如果基于 z ( i ) z^{(i)} z(i)来重构 x ( i ) x^{(i)} x(i),令: x ^ ( i ) = ∑ j = 1 d ′ z j ( i ) w j \widehat{x}^{(i)}=\sum_{j=1}^{d'}z_j^{(i)}w_j x (i)=∑j=1d′zj(i)wj。
x ^ ( i ) \widehat{x}^{(i)} x (i)就是原本d维空间的样本点 x ( i ) x^{(i)} x(i)投影到新的 d ′ d' d′维空间后形成的新样本点在原本d维空间中的位置。
比如:下面这个最简单的例子,原空间是一个二维空间(d=2),把样本x映射到一个一维空间里面去,对应的映射点在二维空间中的坐标为 x ^ \widehat{x} x ,那么x和 x ^ \widehat{x} x 之间的距离当然就是: ∣ ∣ x ^ − x ∣ ∣ 2 2 ||\widehat{x}-x||_2^2 ∣∣x −x∣∣22
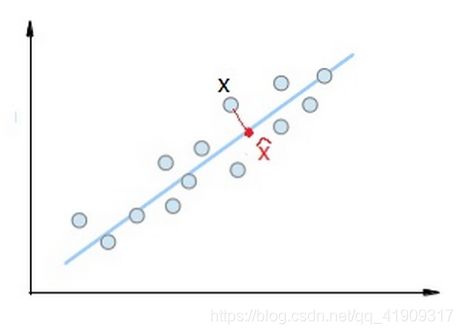
基于最近重构性的优化目标
根据前面说的最近重构性原则,我们要的是所有 n个样本分别与其基于投影重构的样本点间的距离整体最小。
整体距离为:

我们的目标就是最小化整体距离:

因为

其中,C为常数,W是一个 d × d ′ d×d' d×d′的变换矩阵:

它一共有 d ′ d' d′列,每一列都是一个d维的向量 w j w_j wj
换言之, z ( i ) z^{(i)} z(i)是原空间中的样本 x ( i ) x^{(i)} x(i)在新的坐标系 W = ( w 1 , w 2 , . . . , w d ′ ) W=(w_1,w_2,...,w_{d'}) W=(w1,w2,...,wd′)中的坐标向量,于是有: z ( i ) = W T x ( i ) z^{(i)}=W^Tx^{(i)} z(i)=WTx(i)
既然要用W来表示坐标系,样本从原空间到新空间又是不同维度空间中点的线性变换。那么我们大可以从一开始就要求 w j w_j wj是标准正交基,也就是有:
![]()
回到上面的式子:

注意: t r ( M ) tr(M) tr(M)表示方阵M的迹,方型矩阵M的对角线元素之和称为M的迹,而 ∑ i = 1 n x ( i ) x ( i ) T \sum_{i=1}^nx^{(i)}{x^{(i)}}^T ∑i=1nx(i)x(i)T是 d × d d×d d×d的协方差矩阵。
令: X = ( x ( 1 ) , x ( 2 ) , . . . , x ( n ) ) X=(x^{(1)},x^{(2)},...,x^{(n)}) X=(x(1),x(2),...,x(n))
则:

于是,我们的优化目标变成了

这里的约束条件是根据 W 的列是标准正交基来的。如果没有这个约束条件,那就相当于目标函数可以任意拉伸投影向量的模,这样是无法给出最优解的。
基于最大可分性的优化目标
如果从最大可分性出发,应该怎么设定我们的优化目标呢?
根据上面一小节我们知道,原空间样本点在新空间的投影为: z ( i ) = W T x ( i ) z^{(i)}=W^Tx^{(i)} z(i)=WTx(i)
既然要让所有样本点投影后尽量分开,那就应该让新空间中投影点的方差尽量大。比如在下图中,原始数据(白点)投影到黑点所在超平面就比投影到红点所在超平面方差大。
投影点的方差是:
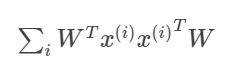
于是优化目标为:

如果对目标函数求负,则是:

正好与基于最近重构性原则构建的优化目标一致!
(要累死了。。。)
