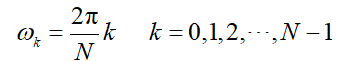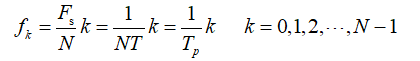实验2 用FFT对信号作频谱分析
MATLAB R2020b v9.9.0 最新中文版(主文件和crack文件都要下载)
主文件:https://cloud.189.cn/t/URJNzqANVVZr (访问码:5glx)
crack文件:https://lanzoux.com/id738gtevbg
密码:yuzhu
IDM插件:https://lanzoux.com/iKndteqln2b
IDM下载器:https://lanzoux.com/iQn1vg9r4gh
提示:暂不提供百度网盘链接!
点我查看公众号网站!
Experiment 2 Spectral analysis using FFT
实验2 用FFT对信号作频谱分析
一、实验安全规则(本实验项目安全注意事项)
1.数字信号处理及DSP应用实验在计算机Matlab上用仿真方式完成,不需要硬件设备,请不要开启计算机桌台上的其它硬件设备;
2.实验可以一人一机单独完成,也可两人一机配合完成,不容许三人一机实验。
二、实验指导
1.实验目的
学习用FFT对连续信号和时域离散信号进行频谱分析(也称谱分析)的方法,了解可能出现的分析误差及其原因,以便正确应用FFT。
2. 实验原理
用FFT对信号作频谱分析是学习数字信号处理的重要内容。 经常需要进行谱分析的信号是模拟信号和时域离散信号。 对信号进行谱分析的重要问题是频谱分辨率D和分析误差。
频谱分辨率直接和FFT的变换区间N有关, 因为FFT能够实现的频率分辨率是2π/N, 因此要求2π/N≤D。 可以根据此式选择FFT的变换区间N。 误差主要来自于用FFT作频谱分析时,得到的是离散谱,而信号(周期信号除外)是连续谱,只有当N较大时,离散谱的包络才能逼近于连续谱,因此N要适当选择大一些。
周期信号的频谱是离散谱,只有用整数倍周期的长度作FFT,得到的离散谱才能代表周期信号的频谱。 如果不知道信号周期,可以尽量选择信号的观察时间长一些。
对模拟信号进行谱分析时,首先要按照采样定理将其变成时域离散信号。如果是模拟周期信号,也应该选取整数倍周期的长度,经过采样后形成周期序列,按照周期序列的谱分析进行。
3. 实验内容、步骤及过程
(1) 复习DFT的定义、 性质和用DFT作谱分析的有关内容。
(2) 复习FFT算法原理与编程思想, 并对照DIT-FFT运算流图和程序框图, 读懂本实验提供的FFT子程序。
(3) 编制信号产生子程序, 产生典型信号供谱分析用。
(4) 编写主程序。
(5) 按实验内容要求, 上机实验, 并写出实验报告。
4.实验数据处理及结论
(1)实验结果截图上传学习通课程作业,对序列进行谱分析:
选择FFT的变换区间N为8和16的两种情况进行频谱分析。分别打印其幅频特性曲线,并进行对比、分析和讨论。
(2)对周期序列进行谱分析
选择FFT的变换区间N为8和16的两种情况分别对以上序列进行频谱分析。分别打印其幅频特性曲线。并进行对比、分析和讨论。
(3)对模拟周期信号进行谱分析:
x6(t)=cos8πt+cos16πt+cos20πt
选择采样频率Fs=64 Hz,变换区间N=16,32,64的三种情况进行谱分析。分别打印其幅频特性,并进行分析和讨论。
- 思考题
(1) 在N=8时, x2(n)和x3(n)的幅频特性会相同吗? 为什么? N=16呢?
(2) 如果周期信号的周期预先不知道, 如何用FFT进行谱分析?
6.实验收获与建议:在撰写实验报告书结尾时,应阐述自己在本实验项目中的收获、体会及对实验项目或实验室工作的建议等。
三、实验参考
1.实验程序清单
实验二程序exp2.m
% 用FFT对信号作频谱分析
%实验内容(1)================================
x1n = [ones(1, 4)];%产生序列向量x1(n)=R4(n)
M=4; xa=1: (M/2); xb=(M/2): -1: 1;
x2n =[xa ,xb]; %产生长度为8的三角波序列x2(n)
x3n =[xb ,xa];
X1k8=fft(x1n, 8); %计算x1n的8点 DFT
X1k16=fft(x1n, 16); %计算x1n的16点DFT
X2k8=fft(x2n, 8); %计算x1n的8点DFT
X2k16=fft(x2n, 16); %计算x1n的16点DFT
X3k8=fft(x3n, 8); %计算x1n的8点DFT
X3k16=fft(x3n, 16); %计算x1n的16点DFT
%以下绘制幅频特性曲线
subplot(2, 2, 1); stem(X1k8);
%绘制8点DFT的幅频特性图
title('(1a) 8点DFT[x_1(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X1k8))])
subplot(2, 2, 3); stem(X1k16);
%绘制16点DFT的幅频特性图
title('(1b)16点DFT[x_1(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X1k16))])
figure(2)
subplot(2, 2, 1); stem(X2k8);
%绘制8点DFT的幅频特性图
title('(2a) 8点DFT[x_2(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X2k8))])
subplot(2, 2, 2); stem(X2k16);
%绘制16点DFT的幅频特性图
title('(2b)16点DFT[x_2(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X2k16))])
subplot(2, 2, 3); stem(X3k8);
%绘制8点DFT的幅频特性图
title('(3a) 8点DFT[x_3(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X3k8))])
subplot(2, 2, 4); stem(X3k16);
%绘制16点DFT的幅频特性图
title('(3b)16点DFT[x_3(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X3k16))])
%实验内容(2)================================
N=8; n=0: N-1; %FFT的变换区间N=8
x4n=cos(pi*n/4);
x5n=cos(pi*n/4)+cos(pi*n/8);
X4k8=fft(x4n); %计算x4n的8点DFT
X5k8=fft(x5n); %计算x5n的8点DFT
N=16; n=0: N-1; %FFT的变换区间N=16
x4n=cos(pi*n/4);
x5n=cos(pi*n/4)+cos(pi*n/8);
X4k16=fft(x4n); %计算x4n的16点DFT
X5k16=fft(x5n); %计算x5n的16点DFT
figure(3)
subplot(2, 2, 1); stem(X4k8);
%绘制8点DFT的幅频特性图
title('(4a) 8点DFT[x_4(n)]');
xlabel('ω/π'); ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X4k8))])
subplot(2, 2, 3); stem(X4k16);
%绘制16点DFT的幅频特性图
title('(4b)16点DFT[x_4(n)]');
xlabel('ω/π'); ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X4k16))])
subplot(2, 2, 2); stem(X5k8);
%绘制8点DFT的幅频特性图
title('(5a) 8点DFT[x_5(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X5k8))])
subplot(2, 2, 4); stem(X5k16);
%绘制16点DFT的幅频特性图
title('(5b)16点DFT[x_5(n)]'); xlabel('ω/π');
ylabel('幅度');
axis([0, 2, 0, 1.2*max(abs(X5k16))])
%实验内容(3)================================
figure(4)
Fs=64; T=1/Fs;
N=16; n=0: N-1; %FFT的变换区间N=16
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);
%对x6(t)16点采样
X6k16=fft(x6nT); %计算x6nT的16点DFT
X6k16=fftshift(X6k16); %将零频率移到频谱中心
Tp=N*T; F=1/Tp; %频率分辨率F
k=-N/2: N/2-1; fk=k*F;
%产生16点DFT对应的采样点频率(以零频率为中心)
subplot(3, 1, 1); stem(fk, abs(X6k16), '.');
box on %绘制8点DFT的幅频特性图
title('(6a) 16点|DFT[x_6(nT)]|'); xlabel('f(Hz)');
ylabel('幅度');
axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k16))]); N=32; n=0: N-1; %FFT的变换区间N=16
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);
%对x6(t)32点采样
X6k32=fft(x6nT); %计算x6nT的32点DFT
X6k32=fftshift(X6k32); %将零频率移到频谱中心
Tp=N*T; F=1/Tp; %频率分辨率F
k=-N/2: N/2-1; fk=k*F;
%产生16点DFT对应的采样点频率(以零频率为中心)
subplot(3, 1, 2); stem(fk, abs(X6k32), '.');
box on %绘制8点DFT的幅频特性图
title('(6b) 32点|DFT[x_6(nT)]|');
xlabel('f(Hz)'); ylabel('幅度');
axis([-N*F/2-1, N*F/2-1,0, 1.2*max(abs(X6k32))])
N=64; n=0: N-1; %FFT的变换区间N=16
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);
%对x6(t)64点采样
X6k64=fft(x6nT); %计算x6nT的64点DFT
X6k64=fftshift(X6k64); %将零频率移到频谱中心
Tp=N*T; F=1/Tp; %频率分辨率F
k=-N/2: N/2-1; fk=k*F;
subplot(3, 1, 3); stem(fk, abs(X6k64), '.');
%产生16点DFT对应的采样点频率(以零频率为中心)subplot(3, 1, 3); stem(fk, abs(X6k64), '.');
box on%绘制8点DFT的幅频特性图
title('(6c) 64点|DFT[x_6(nT)]|');
xlabel('f(Hz)'); ylabel('幅度');
axis([-N*F/2-1,N*F/2-1,0, 1.2*max(abs(X6k64))])
2.实验程序运行结果 实验二程序exp2.m运行结果如图所示。
3.分析与讨论
请注意,用DFT(或FFT)分析频谱和绘制频谱图时,最好将X(k)的自变量k换算成对应的频率并作为横坐标,便于观察频谱。
为了便于读取频率值,最好关于π归一化,即以ω/π作为横坐标。
实验内容(1)
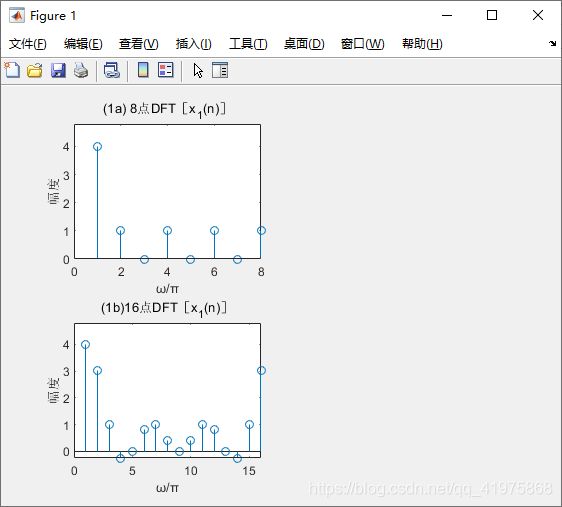
图(1a)和(1b)说明x1(n)=R4(n)的8点DFT和16点DFT分别是x1(n)的频谱函数的8点和16点采样;
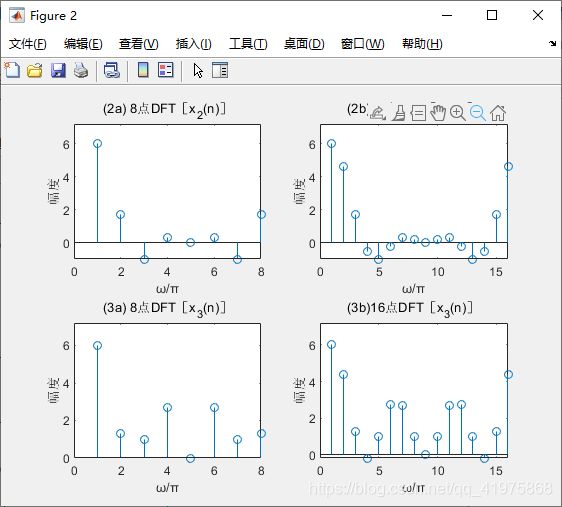
因为x3(n)=x2((n+3))8R8(n),所以,x3(n)与x2(n)的8点DFT的模相等,如图(2a)和(3a)所示。 但是,当N=16时,x3(n)与x2(n)不满足循环移位关系,所以图(2b)和(3b)的模不同。
实验内容(2)
对周期序列谱分析。
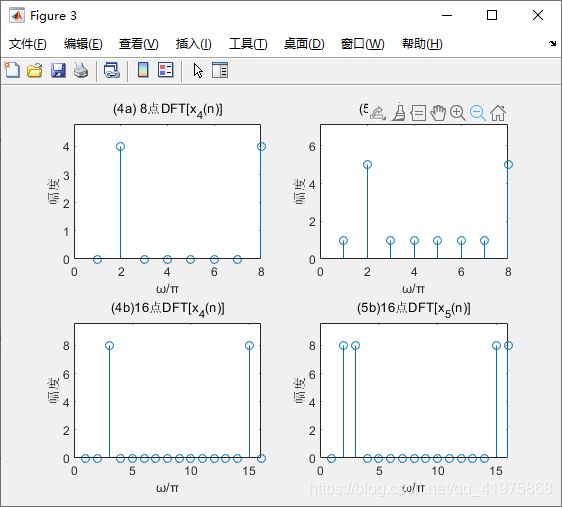
x4(n)=cos n的周期为8,所以N=8和N=16均是其周期的整数倍,得到正确的单一频率正弦波的频谱,仅在0.25π处有1根单一谱线。 如图(4a)和(4b)所示。
x5(n)=cos(πn/4)+cos(πn/8)的周期为16, 所以N=8不是其周期的整数倍, 得到的频谱不正确,如图(5a)所示。 N=16是其一个周期,得到正确的频谱,仅在0.25π和0.125π处有2根单一谱线,如图(5b)所示。
实验内容(3)
对模拟周期信号谱分析。
x6(t)=cos8πt+cos16πt+cos20πt
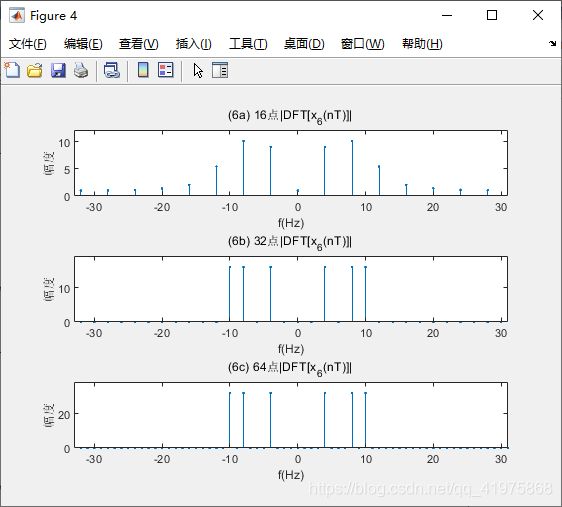
x6(t)有3个频率成分, f1=4 Hz, f2=8 Hz, f3=10 Hz。所以x6(t)的周期为0.5 s。采样频率Fs=64 Hz=16f1=8f2=6.4f3。变换区间N=16时,观察时间Tp=16T=0.25 s,不是x6(t)的整数倍周期, 所以所得频谱不正确,如图(6a)所示。
变换区间N=32,64 时,观察时间Tp=0.5 s,1 s,是x6(t)的整数周期,所以所得频谱正确,如图(6b)和(6c)所示。图中3根谱线正好分别位于4、8、10 Hz处。
变换区间N=64 时, 频谱幅度是变换区间N=32时的2倍, 这种结果正好验证了用DFT对中期序列谱分析的理论。
注意:
(1) 用DFT(或FFT)对模拟信号分析频谱时,最好将X(k)的自变量k换算成对应的模拟频率fk并作为横坐标绘图,以便于观察频谱。这样,不管变换区间N取信号周期的几倍,画出的频谱图中有效离散谐波谱线所在的频率值不变,如图(6b)和(6c)所示。
(2) 本程序直接画出采样序列N点DFT的模值, 实际上分析频谱时最好画出归一化幅度谱, 这样就避免了幅度值随变换区间N变化的缺点。 本实验程序这样绘图只是为了验证用DFT对序列谱分析的理论。