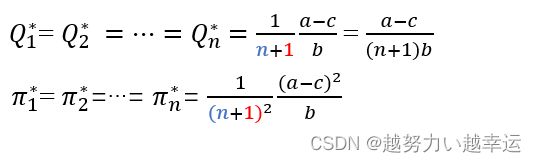【博弈论基础与几大经典模型】古诺模型、斯塔克尔伯格模型Stackelberg Game、价格领导模型、Bertrand模型、Sweezy模型

最近阅读了一篇paper中用到了Stackelberg Game建模，于是找了一些资料先学习以下该模型的理论知识，发现很多学科都是相关的，真是神奇的存在。

什么是博弈论

博弈论(Game theory)又称为对策论，是理性个体之间战略对策的数学模型的研究。通过建立思维模型分析战略游戏中个体的行为，并且研究它们的优化策略。这里的个体，不仅可以指代个人，也可以指代企业等各种需要做出决策的个体。

以下笔记内容对应樊老师的视频课，小白都可以听懂的微观经济学理论，非常棒！

纳什均衡

 1.所有博弈参与人的最佳对策（Best response）集合的交点，通常为纳什均衡点。
 2. 达成纳什均衡后，在其他参与人不改变策略时，任一参与人均无法通过改变自身策略获得更高收益。
 3. 在一个博弈中，可以存在一个以上的纳什均衡点，且不同的均衡点收益可以不同。
 4.有时，参与人可以通过协商来达成更优（帕累托占优)的纳什均衡。
 5． 所有参与人选择同一种策略时可以达到纳什均衡的博弈被称为协调博弈，而在协调博弈中，人们有时可以通过协商来达成一个更优的纳什均衡。
 6.复杂博弈中，可以通过猜测-验证的方法来寻找纳什均衡点。

寡头

特征：产品往往基本一致，也可以有差别；只有几家厂商（两家厂商叫双寡头、双头；多于两家厂商叫多头）；进入行业难；大量买方。
分类：
 1）按厂商行动的方式分为：有勾结的（合作的）；一般研究独立行动的（竞争的，不合作的，这类是主流）
 2）按产品特征分为：一般研究纯粹寡头（产品完全一样）；差别寡头
决策变量
 产量Q 第一家产量$q_1$ 第二家产品$q_2$
 价格P
思维方式
 知己知彼、换位思考、瞻前顾后（逆向归纳法）
厂商数量
 双寡头又叫双头；多头

古诺模型

决策变量为Q，双（多头）势均力敌，目标：
产量：第一家企业产量$Q_1$，第二家企业产量$Q_2$，市场产量$Q=Q_1+Q_2$；
利润：第一家企业利润${\pi }_1$，第二家企业利润${\pi }_2$，市场利润$\pi ={\pi }_1+{\pi }_2$
假设条件：
（1）利润最大化；
（2）两家企业（可以扩展到$n$家）；
（3）同质产品（即企业生产的产品一样）；
（4）生产成本为0（$TC=0$），故利润等于总收益$\pi =TR$（成本可以为正数）；
（5）面临相同的线性市场需求曲线；
（6）所有厂家都知道上述假设，并能推测出市场销量、市场价格和利润，完全信息博弈；
（7）同时决策；同时博弈（静态博弈）；
（8）决策变量是产量。

例（一）：设市场反需求函数为$P=a-bQ$，$Q=Q_1+Q_2$，总成本$T{C}_i=0$，边际成本$M{C}_i=0,i=1,2$，求利润最大化下的$Q_1$，$Q_2$，$P$，${\pi }_1$，${\pi }_2$。

第一家企业的利润
$$\begin{gathered} {\pi }_1(Q_1)=T{R}_1-T{C}_1 \\ =P{Q}_1-0=[a-b(Q_1+Q_2)]Q_1 \\ =a{Q}_1-b{Q}_1^2-b{Q}_1{Q}_2 \end{gathered}$$（等利润线）

利润最大化的一阶条件FOC：$\frac{d{\pi }_1}{d{Q}_1}=a-2b{Q}_1-b{Q}_2=0$
推出：
$Q_1=\frac{a-b{Q}_2}{2b}$(寡头1的反应函数，对应的曲线是反应曲线)

同理可得寡头2的反应函数为：
$Q_2=\frac{a-b{Q}_1}{2b}$

反应曲线

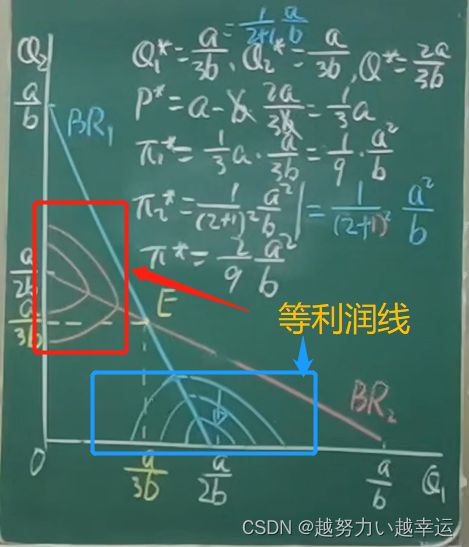
细说反应曲线、等利润线：不同的利润$\pi$对$Q$求导等于0 ，得到相应许多点，这些点连成线得到反应曲线。故等利润线如下图所示，是一簇抛物线。

等利润线

例（二）：设市场反需求函数为$P=a-bQ$，$Q=Q_1+Q_2$，总成本$T{C}_i=c{Q}_i$，边际成本$M{C}_i=c,i=1,2$，求利润最大化。

第一家企业的利润
$$\begin{gathered} {\pi }_1(Q_1)=T{R}_1-T{C}_1 \\ =P{Q}_1-c{Q}_1=[a-b(Q_1+Q_2)]Q_1-c{Q}_1 \\ =(a-c)Q_1-b{Q}_1^2-b{Q}_1{Q}_2 \end{gathered}$$（等利润线）

利润最大化的一阶条件FOC：$\frac{d{\pi }_1}{d{Q}_1}=(a-c)-2b{Q}_1-b{Q}_2=0$
推出：
$Q_1=\frac{(a-c)-b{Q}_2}{2b}$(寡头1的反应函数，对应的曲线是反应曲线)

同理可得寡头2的反应函数为：
$Q_2=\frac{(a-c)-b{Q}_1}{2b}$

进而推出：

例（三）：$n$家厂商，设市场反需求函数为$P=a-bQ$，$Q=Q_1+Q_2+...+Q_n$，总成本$T{C}_i=c{Q}_i$，边际成本$M{C}_i=c,i=1,2,...,n$，求利润最大化。

根据上面总结规律可以推出：

例（四-1）：两家企业组成卡特尔的情况:设市场反需求函数为$P=a-bQ$，求利润最大化。
 将两家企业看成一家
 边际收益$MR=a-2bQ$ 。(来自结论：边际收益与反需求函数的关系，截距一样，斜率是反需求函数的2倍)
 边际成本$M{C}_i=c,i=1,2$
 利润最大化的一阶条件是边际收益=边际成本，所以$a-2bQ=c$
 可以推出$Q^{\ast }=\frac{a-c}{2b}=\frac{1}{2}\frac{a-c}{b}$<$\frac{2}{3}\frac{a-c}{b}$

 所以双寡头被垄断成一家企业时，产量降低了（价格会高）。

  $P^{\ast }=a-b\ast \frac{1}{2}\frac{a-c}{b}=a-\frac{1}{2}(a-c)=\frac{1}{2}(a+c)$

  ${\pi }^{\ast }=P^{\ast }\ast Q^{\ast }-c\ast Q^{\ast }=[\frac{1}{2}(a+c)-c]\ast \frac{1}{2}\frac{a-c}{b}=\frac{1}{4}\frac{(a-c{)}^2}{b}$>$\frac{2}{9}\frac{(a-c{)}^2}{b}$

 所以双寡头被垄断成一家企业时，产量降低了，价格会高，而利润是增加了。

例（四-2）：统一决策，两家企业组成卡特尔的情况:设市场反需求函数为$P=a-bQ$，求利润最大化。

市场利润=两家企业总收益-两家企业总成本即，

$$\begin{gathered} \pi (Q_1,Q_2)=(T{R}_1+T{R}_2)-(T{C}_1+T{C}_2) \\ =P\ast (Q_1+Q_2)-(c{Q}_1+cQ2) \\ =[a-b(Q_1+Q_2)]\ast (Q_1+Q_2)-(c{Q}_1+cQ2) \\ =a{Q}_1+a{Q}_2-c{Q}_1-c{Q}_2-b{Q}_1^2-2b{Q}_1{Q}_2-b{Q}_2^2 \end{gathered}$$

推出$\frac{d\pi }{d{Q}_1}=a-c-2b{Q}_1-2b{Q}_2=0$

   $\frac{d\pi }{d{Q}_2}=a-c-2b{Q}_2-2b{Q}_1=0$
进而推出：
$Q^{\ast }=\frac{a-c}{2b}$
$P^{\ast }=a-b{Q}_1^{\ast }=a-b\frac{a-c}{2b}=\frac{a+c}{2}$
${\pi }^{\ast }=(P-c)Q^{\ast }=a-b{Q}_1^{\ast }=\frac{1}{4}\frac{(a-c{)}^2}{b}$>$\frac{2}{9}\frac{(a-c{)}^2}{b}$

斯塔克尔伯格模型

产量领导模型
领导者-追随者，领导者有先动优势
企业1领导者没有反应函数，企业2追随者有反应函数

假设条件：与古诺模型的区别是第7个假设，Stackelberg假设企业1先决定，企业1的产量$Q_1$，企业2在得知$Q_1$后再决定$Q_2$(动态博弈)。推论：领导者的利润最大化问题应包括追随者的反应函数。

总结：斯塔克伯格博弈Stackelberg Game，是一个两阶段的完全信息动态博弈，博弈的time是序贯的。钙模型的主要思想是领导者（leader）和追随者（followers）双方都是根据对方可能的策略来选择自己的策略以保证自己在对方策略下的利益最大化，从而达到纳什均衡。在该博弈模型中，先作出决策的一方被称为leader，在leader之后，剩余的players根据leader的决策进行决策，被称为followers，然后leader再根据followers的决策对自己的决策进行调整，如此往复，直到达到纳什均衡。

例（一）：设市场反需求函数为$P=100-Q=100-（Q_1+Q_2）$，$Q=Q_1+Q_2$，领导者厂商1 $T{C}_1=1.2Q_1^2+2$，追随者厂商2 $T{C}_2=1.5Q_2^2+8$，求利润最大化下的$Q_1$，$Q_2$，$P$，${\pi }_1$，${\pi }_2$。

解：考虑追随者厂商2
$$\begin{gathered} {\pi }_2=T{R}_2-T{C}_2 \\ =[100-(Q_1+Q_2)]Q_2-(1.5Q_2^2+8) \\ =100Q_2-Q_1{Q}_2-2.5Q_2^2-8 \end{gathered}$$

利润最大化的一阶条件FOC为

$\frac{d{\pi }_2}{d{Q}_2}=100-Q_1-5Q_2=0$

可以推出$Q_2=20-\frac{1}{5}{Q}_1$  (1)

把（1）代入厂商1的利润函数，得出

$$\begin{gathered} {\pi }_1=T{R}_1-T{C}_1 \\ =[100-(Q_1+Q_2)]Q_1-(1.2Q_1^2+2) \\ =100Q_1-Q_1{Q}_2-2.2Q_1^2-2 \\ =80Q_1-2Q_1^2-2 \end{gathered}$$

$\frac{d{\pi }_1}{d{Q}_1}=80-4Q_1=0$

可得$Q_1=20$进而可得$Q_2=16$

$P=100-(Q_1+Q_2)=64$
所以领导者厂商1 $T{C}_1=1.2Q_1^2+2=482$
  追随者厂商2 $T{C}_2=1.5Q_2^2+8=392$
$T{R}_1=P{Q}_1=64\ast 20=1280$
$T{R}_2=P{Q}_2=64\ast 16=1024$
可得：
厂商1的利润${\pi }_1=T{R}_1-T{C}_1=1280-482=798$
厂商2的利润${\pi }_2=T{R}_2-T{C}_2=1024-392=632$

价格领导模型

Leader厂商1按边际收益=边际成本（即$M{R}_1=M{C}_1$）选择$P$，Follower厂商2接受P，并按$P=M{C}_2$生产$Q_2$。Follower相应于完全竞争市场的价格接受者，$P=M{C}_2$决定了Follower的供给曲线。把领导者厂商看成剩余市场的垄断者。

例：市场的需求函数$Q=100-0.5P$，领导者厂商1：$T{C}_1=1.2Q_1^2+6$，追随者厂商2：$T{C}_2=1.5Q_2^2+8$，求利润最大化下的$Q_1$，$Q_2$，$P$，${\pi }_1$，${\pi }_2$。

注：边际成本=总成本变动量/产量变动量。由定义得知边际成本等于总成本（TC）的变化量（△TC）除以对应的产量上的变化量（△Q），即：MC（Q)=△TC（Q）/△Q或MC（Q）=lim=△TC（Q）/△Q=dTC/dQ（其中△Q→0）。

解：考虑厂商2：

  利润最大化原则为 $M{C}_2=P$，即$\frac{dT{C}_2}{d{Q}_2}=3Q=P$，得厂商2得供给函数$S_2=Q_2(P)=\frac{1}{3}P$

  考虑厂商1：

  剩余需求为 $D_1(P)=D(P)-S_2(P)=(100-0.5P)-\frac{1}{3}P=100-\frac{5}{6}P$，可以推出反需求函数为$P=120-\frac{6}{5}{Q}_1$

由反需求函数得到边际收益为$M{R}_1=120-\frac{12}{5}{Q}_1$，

由利润最大化的FOC 边际收益=边际成本 得 $120-\frac{12}{5}{Q}_1=2.4Q_1$，解得$Q_1^{\ast }=25，P^{\ast }=90，Q_2^{\ast }=30，Q^{\ast }=Q_1^{\ast }+Q_2^{\ast }=55$

可得：
厂商1的利润${\pi }_1=T{R}_1-T{C}_1=1494$
厂商2的利润${\pi }_2=T{R}_2-T{C}_2=1342$

注：厂商2有后动优势。

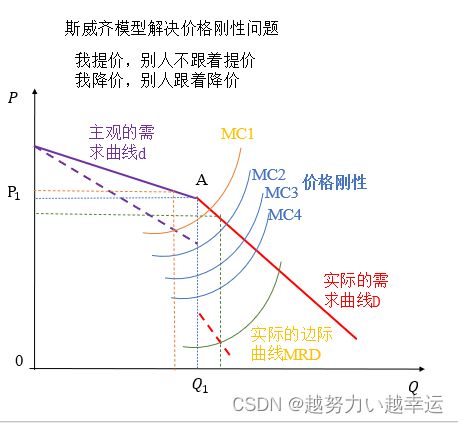
Bertrand模型（伯川德、贝特兰、贝特朗）

两家厂商，产品完全相同，企业成本完全相同，选择变量为P，同时决策，均衡条件：$P_1=P_2=M{C}_1=M{C}_2$

Sweezy模型（斯威齐模型）