深度学习中正则化的理解
在CSDN阅读大佬们的文章,作为一个深度学习小白,收获良多,心生向往。寻思着,一来权当做记笔记,加强记忆;二来说不定未来会有和我一样的萌新遇到和我一样的问题,希望能帮到一二;三来若有大佬对本文所写的纰漏之处批评指正,相比会受益良多。本文大纲主线为吴恩达教授的深度学习系列课程,加上在各论坛阅读的博文与自我理解。第一次发文不懂规矩,参考文献在文末,如果有侵权或者不妥之处,希望大佬们批评,我一定改正。
问题背景
深度学习中可能存在过拟合问题——高方差。这种情况有两个解决方法,一个是正则化,另一个是准备更多的数据,考虑到获取更多数据的成本较高,且某些情况下无法获取更多数据,因此正则化通常有助于避免过拟合或减少网络误差。
正则化的目的是为了防止过拟合,进而增强泛化能力,用“人话”说就是避免利用训练集训练出来的模型过度“迎合”训练集,而导致测试集输入模型后的效果变差。
思路
正则化的英文为Regularization,直译为“规则化”,即通过给模型增加“规则、限制”,从而使模型具有较强的泛化能力,防止过拟合。
在深层神经网络中,理论上只要层数够大,每一层的神经元数量够多,则该深层神经网络完美拟合任意数据集。但是如果深层神经网络模型真的完全拟合了训练集的所有数据,则必然对测试集导致过拟合。正则化的目的是避免过拟合,因此正则化的思路可以概括为:通过一定手段使神经网络中的部分神经元关闭,从而降低神经网络的复杂程度,进而避免过拟合。
分类
常见的正则化方法包括:L0正则化、L1正则化、L2正则化(最常用)、dropout正则化。
除此之外,还有数据扩增、早停法(early stopping)等,由于也可以起到防止过拟合的作用,也被归类为正则化方法。
L2正则化
L2正则化就是在代价函数后面再加上一个正则化项(也称为“权重衰减项”):
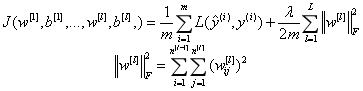
其中 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) \frac{1}{m}\displaystyle\sum_{i=1}^{m} L(\hat{y}^{(i)},y^{(i)}) m1i=1∑mL(y^(i),y(i))就是原始的代价函数,后面一项 λ 2 m ∑ l = 1 L ∣ ∣ w [ l ] ∣ ∣ F 2 \frac{\lambda}{2m}\displaystyle\sum_{l=1}^{L}||w^{[l]}||^{2}_{F} 2mλl=1∑L∣∣w[l]∣∣F2就是L2正则化项。 ∣ ∣ w [ l ] ∣ ∣ F ||w^{[l]}||_{F} ∣∣w[l]∣∣F是参数矩阵的F范数(L2范数),即对各参数的平方和再求平方根。所有F范数的平方和除以训练集的样本大小m,再乘以正则项系数 λ \lambda λ即为L2正则化项。
由于正则化项的存在,我们在使用梯队下降法,求损失函数对w的偏导数时,就会发现偏导数相比于没有正则化项,有所增加:
w [ l ] : = w [ l ] − α ( ∂ J ∂ w [ l ] + λ m w [ l ] ) w^{[l]}:=w^{[l]}-\alpha(\frac{\partial J}{\partial w^{[l]}}+\frac{\lambda}{m}w^{[l]}) w[l]:=w[l]−α(∂w[l]∂J+mλw[l])
因此最终选择时,参数w会变得更小。参数更小,对于模型来说,就意味着更加简单,越简单的模型越不容易产生过拟合现象。直观上理解就是,正则化项 λ \lambda λ设置的足够大,权重矩阵w会随之变小,即更多的神经元权重降低,甚至于彻底消除部分神经元的影响。此时原本复杂的神经网络就会被简化成一个神经元数量较少,但深度不变的网络,网络会从过度拟合(高方差)状态向高偏差、低方差方向发展。
L0、L1正则化
L0、L1正则化与L2正则化类似。把L2正则化项中的L2范数计算替换成L0范数、L1范数计算即可得到L0、L1正则化项。
L0正则化的值是模型参数中非零参数的个数。
L1正则化表示各个参数绝对值之和。
L2正则化标识各个参数的平方的和的开方值。
从直观上看,利用非零参数的个数,可以很好的来选择特征,实现特征稀疏的效果,具体操作时选择参数非零的特征即可。但因为L0正则化很难求解,是个NP难问题,因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似,比L0容易求解,并且也可以实现稀疏的效果。又由于参数值大小和模型复杂度是成正比的,因此复杂的模型,其L1范数就大,最终导致损失函数就大,说明这个模型不够好。
L1正则化与L2正则化的对比
L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。L1在特征选择时候非常有用,而L2就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下,选择L1比较合适,因为它能自动选择特征。而如果所有特征中,大部分特征都能起作用,而且起的作用很平均,那么使用L2也许更合适。
随机失活(dropout)正则化
理解dropout
随机失活正则化存在两个版本:直接和反转,直接dropout不常用,这里只对反转dropout(Inverted Dropout)进行说明。
dropout是指在神经网络的训练过程中,对于神经元,按照一定的概率将其暂时从网络中丢弃。
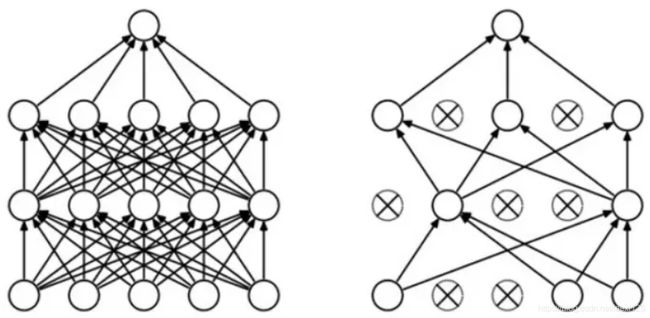
上图为Dropout的可视化表示,左边是应用Dropout之前的网络,右边是应用了Dropout的同一个网络。
dropout如何工作
典型的神经网络其训练流程是将输入通过网络进行正向传导,然后将误差进行反向传播。Dropout就是针对这一过程之中,随机地删除隐藏层的部分单元,进行上述过程。
综合而言,上述过程可以分步骤为:
1.随机删除网络中的一些隐藏神经元,保持输入输出神经元不变;
2.将输入的数据通过修改后的网络进行前向传播,然后将误差通过修改后的网络进行反向传播;
3.对于另外一批的训练样本,重复上述操作(每一次在隐藏神经元这一操作,都“重新随机”);
dropout为何有效
1.由于每次用输入网络的样本进行权值更新时,隐含节点都是以一定概率随机出现,因此不能保证每2个隐含节点每次都同时出现,这样权值的更新不再依赖于有固定关系隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况,减少神经元之间复杂的共适应性。
2.由于每一次都会随机地删除节点,下一个节点的输出不再那么依靠上一个节点,也就是说它在分配权重时,不会给上一层的某一结点非配过多的权重,起到了和L2正则化压缩权重差不多的作用。
3.可以将dropout看作是模型平均的一种,平均一个大量不同的网络。不同的网络在不同的情况下过拟合,虽然不同的网络可能会产生不同程度的过拟合,但是将其公用一个损失函数,相当于对其同时进行了优化,取了平均,因此可以较为有效地防止过拟合的发生。对于每次输入到网络中的样本(可能是一个样本,也可能是一个batch的样本),其对应的网络结构都是不同的,但所有的这些不同的网络结构又同时共享隐含节点的权值,这种平均的架构被发现通常是十分有用的来减少过拟合方法。
dropout使用技巧
1.在可能出现过拟合的网络层使用dropout
2.dropout也可以被用作一种添加噪声的方法,直接对input进行操作。输入层设为更接近1的数,使得输入变化不会太大
dropout缺点
明确定义的损失函数每一次迭代都会下降,而dropout每一次都会随机删除节点,也就是说每一次训练的网络都是不同的,损失函数不再被明确地定义,在某种程度上很难计算,我们失去了调试工具。
当前dropout的使用情况
当前Dropout被大量利用于全连接网络,而且一般人为设置为0.5或者0.3,而在卷积隐藏层由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因,Dropout策略在卷积隐藏层中使用较少。
总体而言,Dropout是一个超参,需要根据具体的网路,具体的应用领域进行尝试。
数据扩增
过拟合问题的产生,是因为可用数据集较少/神经网络复杂度过高。过拟合问题说到底就是神经网络足够复杂可以完全拟合数据集中的全部数据。想要解决这个问题,增强泛化能力,dropout正则化、L2正则化的思路是降低神经网络复杂度;与上述几种方法解决过拟合问题的思路不同,数据扩增解决过拟合问题的中心思想是:增加可用数据集,让现有的神经网络不足以完全拟合全部数据。
数据扩增一般用于图像处理和视频处理领域,常见的方法包括反转、平移、缩放、亮度变化、裁剪、光照等外部影响、颜色变换、模糊、灰度等。
比如,数据集训练模型,用于识别猫。当数据集中数据不足时,可以把每一张图片水平反转,这样就相当于数据集扩充一倍。
通过数据扩增得到的伪训练数据虽然不如额外收集一组新图片效果好,但是扩充后的数据集相比于原始数据集,效果会更好一些。
早停法(early stopping)
在模型训练过程中,我们追求的目标是训练集误差和验证集误差同时尽可能小。
在神经网络训练过程中,训练集误差一般会随着迭代次数的增加不断降低。而验证集误差一般会先随着迭代次数增加而降低,这一过程是模型不断拟合数据的过程。当迭代次数继续增加,验证集误差会开始增加,这是因为模型对训练集过度拟合,泛化能力下降,以至于验证集效果变差。
早停法的核心思想就是在验证集误差“触底反弹”之前,停止训练。使用L2正则化、dropout正则化、数据扩增等方法,即使对模型进行充分训练,也可以一定程度上规避过拟合问题,而早停法解决过拟合问题的方法是:根本不让模型充分训练,让模型在过拟合之前停止训练。
早停法的优点是:只运行一次梯度下降,计算代价较低。相比之下,L2正则化由于要调试正则化参数的值,需要多次运行梯度下降,多次训练模型。
早停法的缺点是:不能独立的处理两个问题,因为提早停止梯度下降,也就是停止了优化代价函数J。因为不再继续尝试降低代价函数J,所以代价函数J的值可能不够小,同时又要避免出现过拟合问题。早停法没有采取不同的方式来解决这两个问题,而是用一个方法同时解决两个问题,这样做的结果就是要考虑的东西会变得更复杂。
总结
本文简单介绍了L2正则化、dropout正则化、数据扩增、早停法等多种正则化方法。其中L2正则化、dropout正则化通过简化神经网络模型解决过拟合问题;数据扩增常用于图片或视频处理,通过制作伪训练数据,达到扩充训练数据集的目的,进而解决了过拟合问题;早停法通过提前结束梯度下降,在牺牲了损失函数J的优化的前提下,达到了避免过拟合的目的。
参考文献
[1].吴恩达-深度学习课程《DeepLearning》
[2].L0,L1,L2正则化浅析,本文为CSDN博主「vivi」的原创文章,遵循 CC 4.0 BY-SA 版权协议,原文链接:https://blog.csdn.net/vividonly/article/details/50723852
[3].深度学习中的正则化(Regularization)),作者:冉冉说,来源:慕课网,链接:http://www.imooc.com/article/69484
[4].Dropout正则化,作者:zzkdev,来源:简书,链接:https://www.jianshu.com/p/257d3da535ab