深度学习机器学习理论知识:范数、稀疏与过拟合合集(1)范数的定义与常用范数介绍
范数、稀疏与过拟合合集(1)范数的定义与常用范数介绍
范数、稀疏与过拟合合集(2)有监督模型下的过拟合与正则化加入后缓解过拟合的原理
范数、稀疏与过拟合合集(3)范数与稀疏化的原理、L0L1L2范数的比较以及数学分析
范数、稀疏与过拟合合集(4)L2范数对condition number较差情况的缓解
范数、稀疏与过拟合合集(5)Dropout原理,操作实现,为什么可以缓解过拟合,使用中的技巧
1、范数简介
范数是具有“长度”概念的函数。在向量空间内,为所有的向量的赋予非零的增长度或者大小。不同的范数,所求的向量的长度或者大小是不同的。
1.1 范数分类
- 向量范数
- 矩阵范数:
1.2 向量范数的定义
假设有一个函数 f f f
f f f完成的映射为 R n → R \mathbb{R}^n\rightarrow \mathbb{R} Rn→R
非负性:对于 ∀ x ∈ R n \forall \boldsymbol{x} \in \mathbb{R}^{n} ∀x∈Rn,满足 f ( x ) ≥ 0 f(\boldsymbol{x}) \geq 0 f(x)≥0,等号当且仅当 x = 0 \boldsymbol{x}=0 x=0时成立
齐次性:对于 ∀ x ∈ R n , ∀ α ∈ R \forall x \in \mathbb R^{n}, \forall \alpha \in \mathbb R ∀x∈Rn,∀α∈R,满足 f ( α x ) = ∣ α ∣ ⋅ f ( x ) f(\alpha \boldsymbol{x})=|\alpha| \cdot f(\boldsymbol{x}) f(αx)=∣α∣⋅f(x)
三角不等式: f ( x + y ) ≤ f ( x ) + f ( y ) f(x+y) \leq f(x)+f(y) f(x+y)≤f(x)+f(y)
则称 f f f为 R n \mathbb R^n Rn上的(向量)范数,通常记为 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣
1.3 矩阵范数的定义
假设有一个函数 f f f
f f f完成的映射为 R n × n → R \mathbb{R}^{n\times n}\rightarrow \mathbb{R} Rn×n→R
非负性:对于 ∀ A ∈ R n × n \forall \boldsymbol{A} \in \mathbb{R}^{n\times n} ∀A∈Rn×n,满足 f ( A ) ≥ 0 f(\boldsymbol{A}) \geq 0 f(A)≥0,等号当且仅当 A = 0 \boldsymbol{A}=0 A=0时成立
齐次性:对于 ∀ A ∈ R n × n , ∀ α ∈ R \forall A \in \mathbb R^{n\times n}, \forall \alpha \in \mathbb R ∀A∈Rn×n,∀α∈R,满足 f ( α A ) = ∣ α ∣ ⋅ f ( A ) f(\alpha \boldsymbol{A})=|\alpha| \cdot f(\boldsymbol{A}) f(αA)=∣α∣⋅f(A)
三角不等式: f ( A + B ) ≤ f ( A ) + f ( B ) f(\boldsymbol{A}+\boldsymbol{B}) \leq f(\boldsymbol{A})+f(\boldsymbol{B}) f(A+B)≤f(A)+f(B)
三角不等式: f ( A B ) ≤ f ( A ) f ( B ) f(\boldsymbol{A}\boldsymbol{B}) \leq f(\boldsymbol{A})f(\boldsymbol{B}) f(AB)≤f(A)f(B)
则称 f f f为 R n × n \mathbb R^{n\times n } Rn×n上的(矩阵)范数,通常记为 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣
2、常用向量范数
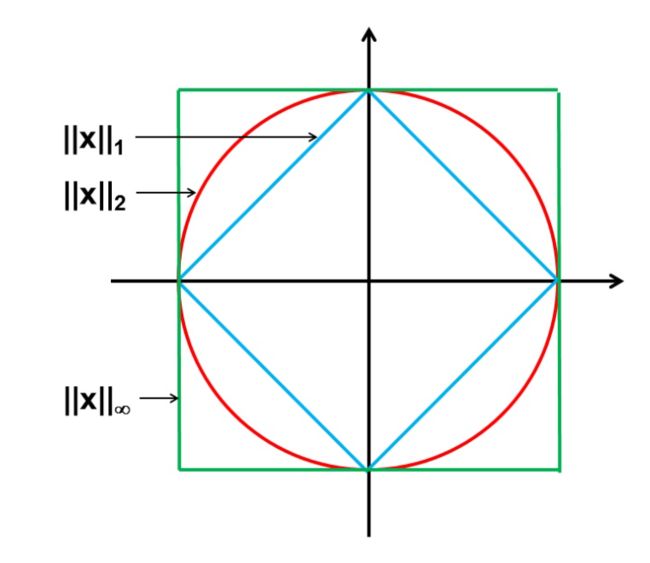
2.1 L p L_p Lp范数:
一般将任意向量 x \boldsymbol{x} x的 L p L_p Lp范数定义为
∥ x ∥ p = ∑ i ∣ x i ∣ p p \|\boldsymbol{x}\|_{p}=\sqrt[p]{\sum_{i}\left|x_{i}\right|^{p}} ∥x∥p=pi∑∣xi∣p
2.2 L 0 L_0 L0范数:向量 x \boldsymbol{x} x中非零元素的个数
∥ x ∥ 0 = ∑ i ∣ x i ∣ 0 0 \|\boldsymbol{x}\|_{0}=\sqrt[0]{\sum_{i}\left|x_{i}\right|^{0}} ∥x∥0=0i∑∣xi∣0
等同于如下计算公式
∥ x ∥ 0 = # ( i ∣ x i ≠ 0 ) \|\boldsymbol{x}\|_{0}=\#\left(i \mid x_{i} \neq 0\right) ∥x∥0=#(i∣xi=0)
在诸多机器学习模型中,比如压缩感知 (compressive sensing),我们很多时候希望最小化向量的 L 0 L_0 L0范数。一个标准的 L 0 L_0 L0范数优化问题往往可以写成如下形式:
min ∥ x ∥ 0 s.t. A x = b \begin{array}{c} \min \|\boldsymbol{x}\|_{0} \\ \text { s.t. } A \boldsymbol{x}=\boldsymbol{b} \end{array} min∥x∥0 s.t. Ax=b
然而,由于 L 0 L_0 L0范数仅仅表示向量中非0元素的个数,因此,这个优化模型在数学上被认为是一个NP-hard问题,即直接求解它很复杂、也不可能找到解。
需要注意的是,正是由于该类优化问题难以求解,因此,压缩感知模型是将 L 0 L_0 L0范数最小化问题转换成 L 1 L_1 L1范数最小化问题。
2.2 L 1 L_1 L1范数:向量中所有元素绝对值之和
也称为稀疏规则化算子(Lasso regularization),是 L 0 L_0 L0范数的最优凸近似。
∥ x ∥ 1 = ∑ i ∣ x i ∣ \|\boldsymbol{x}\|_{1}=\sum_{i}\left|x_{i}\right| ∥x∥1=i∑∣xi∣
一个 L 1 L_1 L1范数优化问题为
min ∥ x ∥ 1 s.t. A x = b \begin{array}{c} \min \|\boldsymbol{x}\|_{1} \\ \text { s.t. } A \boldsymbol{x}=\boldsymbol{b} \end{array} min∥x∥1 s.t. Ax=b
这个问题相比于 L 0 L_0 L0范数优化问题更容易求解,借助现有凸优化算法(线性规划或是非线性规划),就能够找到我们想要的可行解。鉴于此,依赖于 L 1 L_1 L1范数优化问题的机器学习模型如压缩感知就能够进行求解了。
2.3 L 2 L_2 L2范数:向量(或矩阵)的元素平方和开根号
L 2 L_2 L2范数又称Euclidean范数或者Frobenius范数,也表示向量模长,即
∥ x ∥ 2 = ∑ i x i 2 \|\boldsymbol{x}\|_{2}=\sqrt{\sum_{i} x_{i}^{2}} ∥x∥2=i∑xi2
L 2 L_2 L2范数的优化模型如下:
min ∥ x ∥ 2 s.t. A x = b \begin{array}{c} \min \|\boldsymbol{x}\|_{2} \\ \text { s.t. } A \boldsymbol{x}=\boldsymbol{b} \end{array} min∥x∥2 s.t. Ax=b
2.4 L ∞ L_\infty L∞范数:向量元素绝对值中最大值
lim k → ∞ ( ∑ i = 1 n ∣ p i − q i ∣ k ) 1 / k \lim _{k \rightarrow \infty}\left(\sum_{i=1}^{n}\left|p_{i}-q_{i}\right|^{k}\right)^{1 / k} k→∞lim(i=1∑n∣pi−qi∣k)1/k
3、常用矩阵范数
对于矩阵 A ∈ R m × n A\in \mathbb{R}^{m\times n} A∈Rm×n
3.1 1-范数:列和范数
即所有矩阵列向量绝对值之和的最大值
∥ A ∥ 1 = max j ∑ i = 1 m ∣ a i , j ∣ \|A\|_{1}=\max _{j} \sum_{i=1}^{m}\left|a_{i, j}\right| ∥A∥1=jmaxi=1∑m∣ai,j∣
3.2 2-范数:谱范数
∥ A ∥ 2 = λ 1 \|A\|_{2}=\sqrt{\lambda_{1}} ∥A∥2=λ1
λ 1 \lambda_{1} λ1表示 A T A A^{T} A ATA的最大特征值的开平方
3.3 ∞ \infty ∞-范数:行和范数
∥ A ∥ ∞ = max i ∑ j = 1 m ∣ a i , j ∣ \|A\|_{\infty}=\max _{i} \sum_{j=1}^{m}\left|a_{i, j}\right| ∥A∥∞=imaxj=1∑m∣ai,j∣
即所有矩阵行向量绝对值之和的最大值
3.4 F-范数:Frobenius范数
∥ A ∥ F = ( ∑ i = 1 m ∑ j = 1 n a i , j 2 ) 1 2 \|A\|_{F}=\left(\sum_{i=1}^{m} \sum_{j=1}^{n} a_{i, j}^{2}\right)^{\frac{1}{2}} ∥A∥F=(i=1∑mj=1∑nai,j2)21
即矩阵元素绝对值的平方和再开平方
LAST、参考文献
各种范数的解释_u011484045的专栏-CSDN博客
如何通俗易懂地解释「范数」? - 知乎
范数_weixin_34233618的博客-CSDN博客
范数、L1范数和L2范数的基本概念_lioncv的专栏-CSDN博客_l1范数的定义
过拟合以及正则化(L0,L1,L2范数)_yeal-CSDN博客
谱范数的理解与论述_MathThinker的博客-CSDN博客
向量范数与矩阵范数 - 知乎
L1范数和L2范数的区别 - 程序员大本营
L1范数与L2范数的区别 - 知乎
范数、L1范数和L2范数的基本概念_lioncv的专栏-CSDN博客_l1范数的定义
机器学习中的范数规则化之(一)L0、L1与L2范数_bitcarmanlee的博客-CSDN博客
L1范数与L2范数的区别_不二的博客-CSDN博客_l2范数