蓝桥杯-九宫重排（python）

蓝桥杯-九宫重排（python）

题目描述

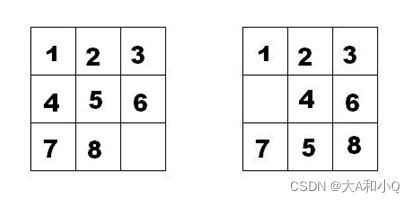
  如下面第一个图的九宫格中，放着 1~8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动，可以形成第二个图所示的局面。

我们把第一个图的局面记为：12345678.
把第二个图的局面记为：123.46758
显然是按从上到下，从左到右的顺序记录数字，空格记为句点。
本题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出-1。
输入
输入第一行包含九宫的初态，第二行包含九宫的终态。
输出
输出最少的步数，如果不存在方案，则输出-1。
样例输入

12345678.
123.46758 

样例输出

3

思路和总结：

  刚开始采用dfs，但因为这道题的解空间较深，容易超时，所以换成了bfs。
  刚开始写bfs还是会超时，于是进行改进，将搜索过的结点转化成hash值存储在serached数列中，多通过了一个样例，但还有超时的。
去查找资料找到C语言网-九宫重排题解。
  对比自己代码与其代码的差异之处，发现了以下几点python编程中可以借鉴的地方：

1、一维数组通过坐标转化映射为二维数组，比直接用二维数组更快。

2、将搜索过的结点以键值对的方式存在字典当中，因为python的字典实现高效，查看键是否在字典中时不需要遍历所有的键值对。

3、在分类讨论时，可以将不同情况下的变化量提取出来用数组表示，遍历数组来对不同情况写相同的代码，而不是直接向上下左右前进四种情况都分别写一次代码。

4、通过运用divmod获得一维数组表示的二维数组下标。

5、交换a、b可以用：a，b=b，a。就省略了中间的temp。

6、[element for row in temp for element in row]

一起来欣赏一下大佬的代码：

def bfs():
    global start, end, cache_state
    stack = [start]
    while stack:
        state = stack.pop(0)
        for direction in around:
            i, j = divmod(state.index('.'), 3)
            if 0 <= i + direction[0] < 3 and 0 <= j + direction[1] < 3:
                # temp = [list(state[3 * k:3 * k + 3]) for k in range(3)]
                # temp[i][j], temp[i + direction[0]][j + direction[1]] = temp[i + direction[0]][j + direction[1]], temp[i][j]
                # temp = ''.join(element for row in temp for element in row)
                temp = list(state)
                idx_0, idx_1 = 3 * i + j, 3 * (i + direction[0]) + j + direction[1]
                temp[idx_0], temp[idx_1] = temp[idx_1], temp[idx_0]
                temp = ''.join(temp)
                if temp not in cache_state:
                    cache_state.setdefault(temp, cache_state[state] + 1)
                    stack.append(temp)
                    if temp == end:
                        return cache_state[end]
 
                         
start, end = [input().strip() for _ in range(2)]
cache_state, around = {start: 0}, [[-1, 0], [0, -1], [1, 0], [0, 1]]
print(bfs())

不好意思地贴一下我自己的代码：

##while True:
s = input()
ls1 = list(s)
s = input()
ls2 = list(s)

queue = list()
# 初始化
i, j = divmod(ls1.index("."), 3)
dot = [i,j]
steps = 0
searched = {"".join(ls1):None}
queue.append([ls1[:], dot[:], steps])
while len(queue)!=0:
    ls1, dot, steps = queue.pop(0)
    if ls1 != ls2 and steps < 81:
        # 向左走
        if dot[1] != 0:
            # 产生结点并加入队列
            ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]-1]=ls1[dot[0]*3+dot[1]-1], ls1[dot[0]*3+dot[1]]
            dot[1] -= 1
            temp = "".join(ls1)
            if temp not in searched:
                searched[temp] = None
                queue.append([ls1[:], dot[:], steps+1])
            ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]+1]=ls1[dot[0]*3+dot[1]+1], ls1[dot[0]*3+dot[1]]
            dot[1] += 1
        # 向右走
        if dot[1] != 2:
            # 产生结点并加入队列
            ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]+1]=ls1[dot[0]*3+dot[1]+1], ls1[dot[0]*3+dot[1]]
            dot[1] += 1
            temp = "".join(ls1)
            if temp not in searched:
                searched[temp] = None
                queue.append([ls1[:], dot[:], steps+1])
            ls1[dot[0]*3+dot[1]], ls1[dot[0]*3+dot[1]-1]=ls1[dot[0]*3+dot[1]-1], ls1[dot[0]*3+dot[1]]
            dot[1] -= 1
        # 向上走
        if dot[0] != 0:
            # 产生结点并加入队列
            ls1[dot[0]*3+dot[1]], ls1[(dot[0]-1)*3+dot[1]]=ls1[(dot[0]-1)*3+dot[1]], ls1[dot[0]*3+dot[1]]
            dot[0] -= 1
            temp = "".join(ls1)
            if temp not in searched:
                searched[temp] = None
                queue.append([ls1[:], dot[:], steps+1])
            ls1[dot[0]*3+dot[1]], ls1[(dot[0]+1)*3+dot[1]]=ls1[(dot[0]+1)*3+dot[1]], ls1[dot[0]*3+ dot[1]]
            dot[0] += 1
        # 向下走
        if dot[0] != 2:
            # 产生结点并加入队列
            ls1[dot[0]*3+dot[1]], ls1[(dot[0]+1)*3+dot[1]]=ls1[(dot[0]+1)*3+dot[1]], ls1[dot[0]*3+dot[1]]
            dot[0] += 1
            temp = "".join(ls1)
            if temp not in searched:
                searched[temp] = None
                queue.append([ls1[:], dot[:], steps+1])
            ls1[dot[0]*3+dot[1]], ls1[(dot[0]-1)*3+dot[1]]=ls1[(dot[0]-1)*3+dot[1]], ls1[dot[0]*3+dot[1]]
            dot[0] -= 1
    else:
        break

if steps == 81:
    print(-1)
else:
    print(steps)

  改进之后的程序在C语言网运行是没问题的，但在蓝桥杯官网却有两个超时，希望有能人志士指点迷津。

参考链接：
C语言网-九宫重排题解